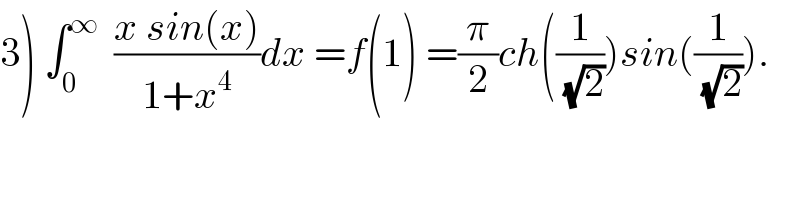Menu Close

let-f-x-0-x-sinx-a-2-x-4-dx-with-a-gt-0-1-find-a-explicit-form-of-f-a-2-find-g-a-0-xsinx-a-2-x-4-2-dx-3-find-the-value-of-0-x-sinx-x-4-1-d

Tinku Tara 0 Comments
Pin




Question Number 44466 by maxmathsup by imad last updated on 29/Sep/18
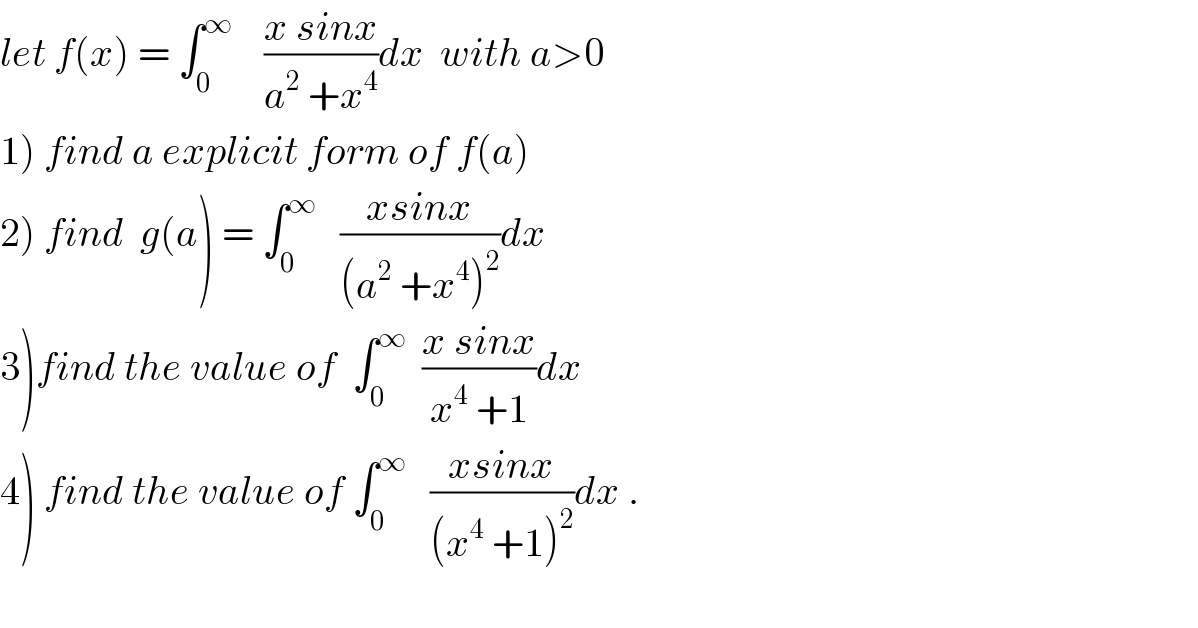
let f(x) = ∫_0 ^∞ ((x sinx)/(a^2 +x^4 ))dx with a>0 1) find a explicit form of f(a) 2) find g(a) = ∫_0 ^∞ ((xsinx)/((a^2 +x^4 )^2 ))dx 3)find the value of ∫_0 ^∞ ((x sinx)/(x^4 +1))dx 4) find the value of ∫_0 ^∞ ((xsinx)/((x^4 +1)^2 ))dx .
$${let}\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{x}\:{sinx}}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{4}} }{dx}\:\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({a}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:\:{g}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{xsinx}}{\left({a}^{\mathrm{2}} \:+{x}^{\mathrm{4}} \right)^{\mathrm{2}} }{dx} \\ $$$$\left.\mathrm{3}\right){find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}\:{sinx}}{{x}^{\mathrm{4}} \:+\mathrm{1}}{dx} \\ $$$$\left.\mathrm{4}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{xsinx}}{\left({x}^{\mathrm{4}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:. \\ $$$$ \\ $$
Commented by abdo.msup.com last updated on 29/Sep/18
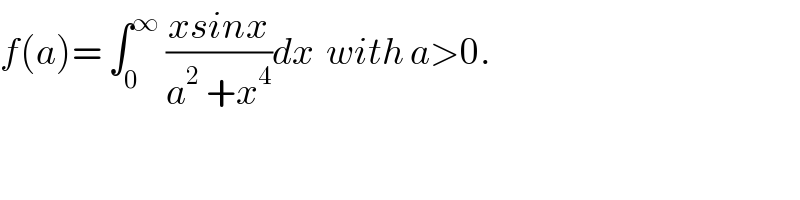
f(a)= ∫_0 ^∞ ((xsinx)/(a^2 +x^4 ))dx with a>0.
$${f}\left({a}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\frac{{xsinx}}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{4}} }{dx}\:\:{with}\:{a}>\mathrm{0}. \\ $$
Commented by maxmathsup by imad last updated on 03/Oct/18
1) we have f(a) =∫_0 ^∞ ((xsin(x))/(a^2 +x^4 ))dx ⇒2f(a) =∫_(−∞) ^(+∞) ((xsin(x))/(a^2 +x^4 ))dx =Im( ∫_(−∞) ^(+∞) ((x e^(ix) )/(a^2 +x^4 ))dx) changement x =(√a)t give I=∫_(−∞) ^(+∞) ((x e^(ix) )/(a^2 +x^4 ))dx = ∫_(−∞) ^(+∞) (((√a)t e^(i(√a)t) )/(a^2 +a^2 t^4 )) (√a)dt =(1/a) ∫_(−∞) ^(+∞) ((t e^(i(√a)t) )/(t^4 +1))dt ⇒ a I = ∫_(−∞) ^(+∞) ((t e^(i(√a)t) )/(t^4 +1))dt let consider the complex function ϕ(z) =((z e^(i(√a)z) )/(z^4 +1)) ⇒ϕ(z) =((z e^(i(√a)z) )/((z^2 −i)(z^2 +i))) =((z e^(i(√a)z) )/((z−e^((iπ)/4) )(z+e^((iπ)/4) )(z−e^(−((iπ)/4)) )(z+e^((iπ)/4) ))) so the poles of ϕ are +^− e^((iπ)/4) and +^− e^(−((iπ)/4)) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,e^((iπ)/4) ) +Res(ϕ,−e^(−((iπ)/4)) )} but Res(ϕ, e^((iπ)/4) ) =lim_(z→e^((iπ)/4) ) (z−e^((iπ)/4) )ϕ(z) =((e^((iπ)/4) e^(i(√a)e^((iπ)/4) ) )/(2 e^((iπ)/4) (2i))) =(1/(4i)) e^(i(√a)((1/( (√2)))+(i/( (√2))))) =(1/(4i)) e^(−((√a)/( (√2) ))) e^(i((√a)/( (√2)))) Res(ϕ, −e^(−((iπ)/4)) ) =lim_(z→−e^(−((iπ)/4)) ) (z+e^(−((iπ)/4)) )ϕ(z) = ((e^(−((iπ)/4)) e^(i(√a) e^(−((iπ)/4)) ) )/((−2i)(−2e^(−((iπ)/4)) ))) =(1/(4i)) e^(i(√a){(1/( (√2)))−(i/( (√2)))}) =(1/(4i)) e^((√a)/( (√2))) e^(i((√a)/( (√(2 ))))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ (1/(4i)) e^(−((√a)/( (√2)))) e^(i((√a)/( (√2)))) +(1/(4i)) e^((√a)/( (√2))) e^(i((√a)/( (√2)))) } =(π/2) e^(i((√a)/( (√2)))) { e^((√a)/( (√2))) +e^(−((√a)/( (√2)))) } =πch(((√a)/( (√2)))) {cos(((√a)/( (√2))))+i sin(((√a)/( (√2))))} ⇒ I =(π/a)ch(((√a)/( (√2)))){cos(((√a)/( (√2))))+isin(((√a)/( (√2))))} ⇒2f(a) =(π/a)ch(((√a)/( (√2))))sin(((√a)/( (√2)))) ⇒ f(a) =(π/(2a)) ch(((√a)/( (√2))))sin(((√a)/( (√2)))) with a>0 .
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{xsin}\left({x}\right)}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{4}} }{dx}\:\:\Rightarrow\mathrm{2}{f}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\:\frac{{xsin}\left({x}\right)}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{4}} }{dx} \\ $$$$={Im}\left(\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{x}\:{e}^{{ix}} }{{a}^{\mathrm{2}} \:+{x}^{\mathrm{4}} }{dx}\right)\:\:{changement}\:{x}\:=\sqrt{{a}}{t}\:{give} \\ $$$${I}=\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{x}\:{e}^{{ix}} }{{a}^{\mathrm{2}} \:+{x}^{\mathrm{4}} }{dx}\:=\:\int_{−\infty} ^{+\infty} \:\:\frac{\sqrt{{a}}{t}\:{e}^{{i}\sqrt{{a}}{t}} }{{a}^{\mathrm{2}} \:+{a}^{\mathrm{2}} {t}^{\mathrm{4}} }\:\sqrt{{a}}{dt}\:=\frac{\mathrm{1}}{{a}}\:\int_{−\infty} ^{+\infty} \:\:\frac{{t}\:{e}^{{i}\sqrt{{a}}{t}} }{{t}^{\mathrm{4}} \:+\mathrm{1}}{dt}\:\Rightarrow \\ $$$${a}\:{I}\:=\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{t}\:{e}^{{i}\sqrt{{a}}{t}} }{{t}^{\mathrm{4}} \:+\mathrm{1}}{dt}\:{let}\:\:{consider}\:{the}\:{complex}\:{function} \\ $$$$\varphi\left({z}\right)\:=\frac{{z}\:{e}^{{i}\sqrt{{a}}{z}} }{{z}^{\mathrm{4}} \:+\mathrm{1}}\:\Rightarrow\varphi\left({z}\right)\:=\frac{{z}\:{e}^{{i}\sqrt{{a}}{z}} }{\left({z}^{\mathrm{2}} −{i}\right)\left({z}^{\mathrm{2}} \:+{i}\right)}\:=\frac{{z}\:{e}^{{i}\sqrt{{a}}{z}} }{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$${so}\:{the}\:{poles}\:{of}\:\varphi\:{are}\:\overset{−} {+}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:{and}\:\overset{−} {+}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\}\:{but} \\ $$$${Res}\left(\varphi,\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:={lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{4}}} } \:\:\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\varphi\left({z}\right)\:=\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\:{e}^{{i}\sqrt{{a}}{e}^{\frac{{i}\pi}{\mathrm{4}}} } }{\mathrm{2}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \left(\mathrm{2}{i}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}{i}}\:{e}^{{i}\sqrt{{a}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{i}}\:\:{e}^{−\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}\:}} \:{e}^{{i}\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}} \\ $$$${Res}\left(\varphi,\:−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:={lim}_{{z}\rightarrow−{e}^{−\frac{{i}\pi}{\mathrm{4}}} } \:\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\varphi\left({z}\right) \\ $$$$=\:\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:{e}^{{i}\sqrt{{a}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} } }{\left(−\mathrm{2}{i}\right)\left(−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}\:=\frac{\mathrm{1}}{\mathrm{4}{i}}\:{e}^{{i}\sqrt{{a}}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{{i}}{\:\sqrt{\mathrm{2}}}\right\}} \:=\frac{\mathrm{1}}{\mathrm{4}{i}}\:{e}^{\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}} \:{e}^{{i}\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}\:\:\:}}} \\ $$$$\Rightarrow\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\frac{\mathrm{1}}{\mathrm{4}{i}}\:{e}^{−\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}} \:{e}^{{i}\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}} \:\:\:+\frac{\mathrm{1}}{\mathrm{4}{i}}\:{e}^{\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}} \:\:{e}^{{i}\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}} \right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\:{e}^{{i}\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}} \:\left\{\:{e}^{\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}} \:+{e}^{−\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}} \right\}\:=\pi{ch}\left(\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}\right)\:\left\{{cos}\left(\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}\right)+{i}\:{sin}\left(\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}\right)\right\}\:\Rightarrow \\ $$$${I}\:=\frac{\pi}{{a}}{ch}\left(\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}\right)\left\{{cos}\left(\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}\right)+{isin}\left(\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}\right)\right\}\:\Rightarrow\mathrm{2}{f}\left({a}\right)\:=\frac{\pi}{{a}}{ch}\left(\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}\right){sin}\left(\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}\right)\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\frac{\pi}{\mathrm{2}{a}}\:{ch}\left(\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}\right){sin}\left(\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}\right)\:\:{with}\:{a}>\mathrm{0}\:. \\ $$
Commented by maxmathsup by imad last updated on 04/Oct/18
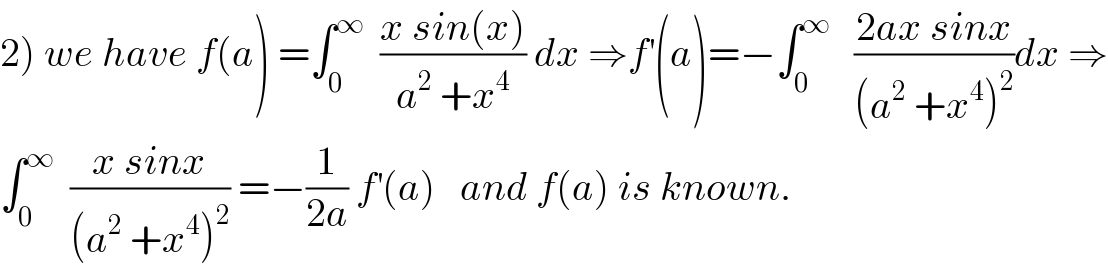
2) we have f(a) =∫_0 ^∞ ((x sin(x))/(a^2 +x^4 )) dx ⇒f^′ (a)=−∫_0 ^∞ ((2ax sinx)/((a^2 +x^4 )^2 ))dx ⇒ ∫_0 ^∞ ((x sinx)/((a^2 +x^4 )^2 )) =−(1/(2a)) f^′ (a) and f(a) is known.
$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}\:{sin}\left({x}\right)}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{4}} }\:{dx}\:\Rightarrow{f}^{'} \left({a}\right)=−\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{ax}\:{sinx}}{\left({a}^{\mathrm{2}} \:+{x}^{\mathrm{4}} \right)^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}\:{sinx}}{\left({a}^{\mathrm{2}} \:+{x}^{\mathrm{4}} \right)^{\mathrm{2}} }\:=−\frac{\mathrm{1}}{\mathrm{2}{a}}\:{f}^{'} \left({a}\right)\:\:\:{and}\:{f}\left({a}\right)\:{is}\:{known}. \\ $$
Commented by maxmathsup by imad last updated on 04/Oct/18
3) ∫_0 ^∞ ((x sin(x))/(1+x^4 ))dx =f(1) =(π/2)ch((1/( (√2))))sin((1/( (√2)))).
$$\left.\mathrm{3}\right)\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}\:{sin}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{4}} }{dx}\:={f}\left(\mathrm{1}\right)\:=\frac{\pi}{\mathrm{2}}{ch}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right){sin}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right). \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *