Question Number 98943 by mathmax by abdo last updated on 17/Jun/20
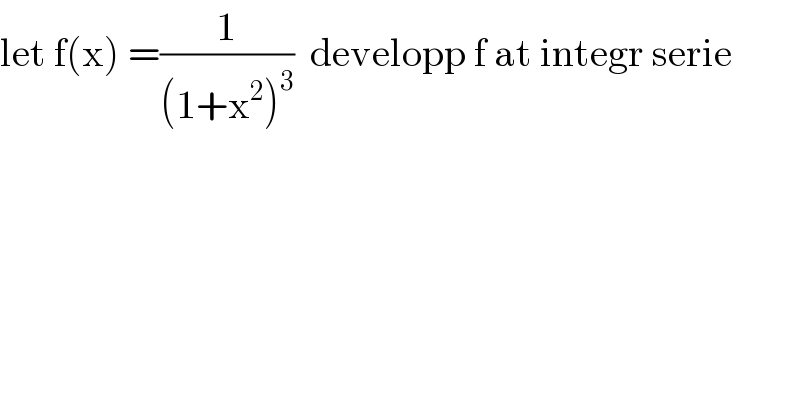
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} }\:\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{integr}\:\mathrm{serie} \\ $$
Answered by maths mind last updated on 17/Jun/20
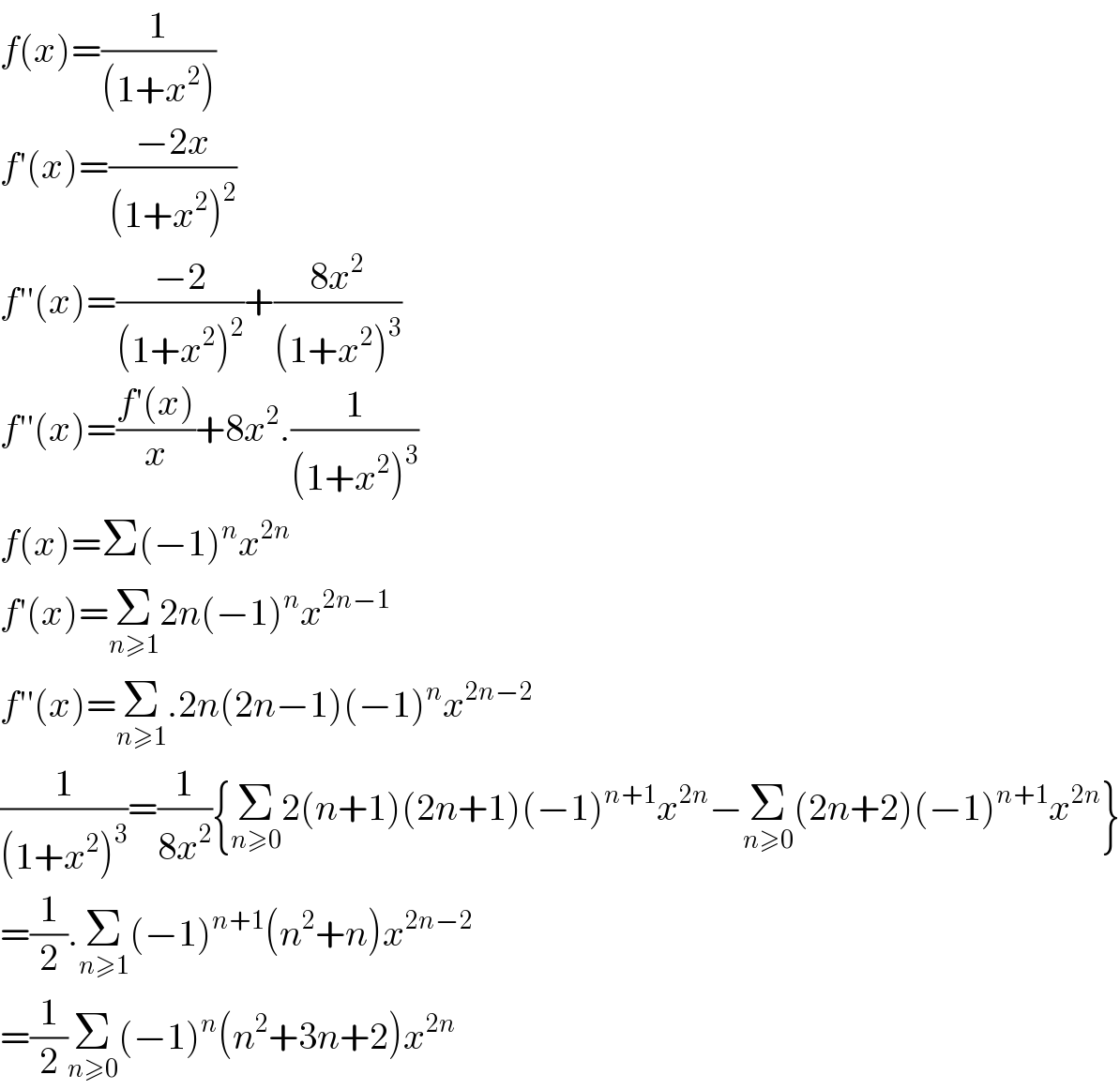
$${f}\left({x}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$${f}'\left({x}\right)=\frac{−\mathrm{2}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${f}''\left({x}\right)=\frac{−\mathrm{2}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }+\frac{\mathrm{8}{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$${f}''\left({x}\right)=\frac{{f}'\left({x}\right)}{{x}}+\mathrm{8}{x}^{\mathrm{2}} .\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$${f}\left({x}\right)=\Sigma\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} \\ $$$${f}'\left({x}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\mathrm{2}{n}\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}−\mathrm{1}} \\ $$$${f}''\left({x}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}.\mathrm{2}{n}\left(\mathrm{2}{n}−\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}−\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{2}} }\left\{\underset{{n}\geqslant\mathrm{0}} {\sum}\mathrm{2}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {x}^{\mathrm{2}{n}} −\underset{{n}\geqslant\mathrm{0}} {\sum}\left(\mathrm{2}{n}+\mathrm{2}\right)\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {x}^{\mathrm{2}{n}} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \left({n}^{\mathrm{2}} +{n}\right){x}^{\mathrm{2}{n}−\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} \left({n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2}\right){x}^{\mathrm{2}{n}} \\ $$
Commented by mathmax by abdo last updated on 17/Jun/20

$$\mathrm{thanks}\:\mathrm{sir}. \\ $$
Answered by mathmax by abdo last updated on 17/Jun/20
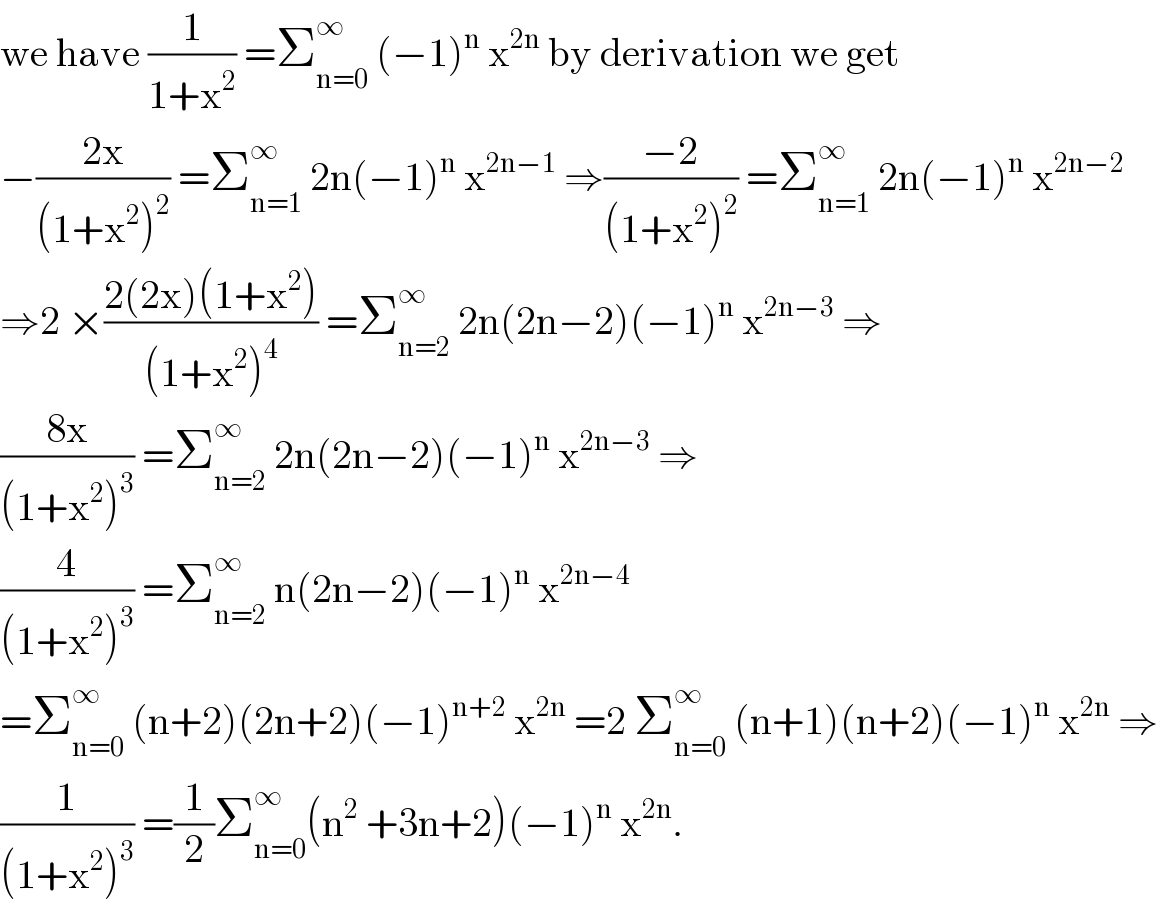
$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} \:\mathrm{by}\:\mathrm{derivation}\:\mathrm{we}\:\mathrm{get} \\ $$$$−\frac{\mathrm{2x}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{2n}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}−\mathrm{1}} \:\Rightarrow\frac{−\mathrm{2}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{2n}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}−\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\:×\frac{\mathrm{2}\left(\mathrm{2x}\right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{4}} }\:=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\mathrm{2n}\left(\mathrm{2n}−\mathrm{2}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}−\mathrm{3}} \:\Rightarrow \\ $$$$\frac{\mathrm{8x}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} }\:=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\mathrm{2n}\left(\mathrm{2n}−\mathrm{2}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}−\mathrm{3}} \:\Rightarrow \\ $$$$\frac{\mathrm{4}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} }\:=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\mathrm{n}\left(\mathrm{2n}−\mathrm{2}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}−\mathrm{4}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{2n}+\mathrm{2}\right)\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{2}} \:\mathrm{x}^{\mathrm{2n}} \:=\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} \:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(\mathrm{n}^{\mathrm{2}} \:+\mathrm{3n}+\mathrm{2}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} . \\ $$
