Question Number 104919 by mathmax by abdo last updated on 24/Jul/20
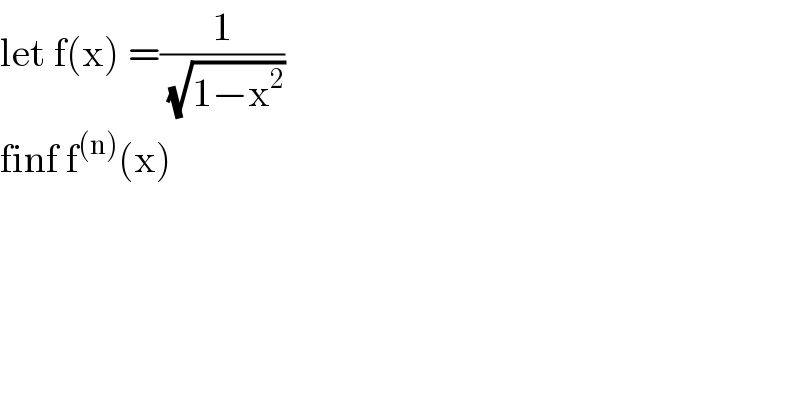
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{finf}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right) \\ $$
Commented by malwaan last updated on 25/Jul/20

$${can}\:{you}\:{post}\:{the}\:{steps}\:{please} \\ $$$${thank}\:{you}\:{sir}\:{shikari} \\ $$
Commented by Dwaipayan Shikari last updated on 24/Jul/20
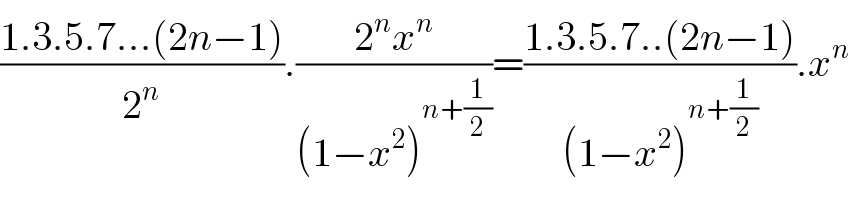
$$\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}.\mathrm{7}…\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{2}^{{n}} }.\frac{\mathrm{2}^{{n}} {x}^{{n}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} }=\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}.\mathrm{7}..\left(\mathrm{2}{n}−\mathrm{1}\right)}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} }.{x}^{{n}} \\ $$
Commented by Dwaipayan Shikari last updated on 25/Jul/20
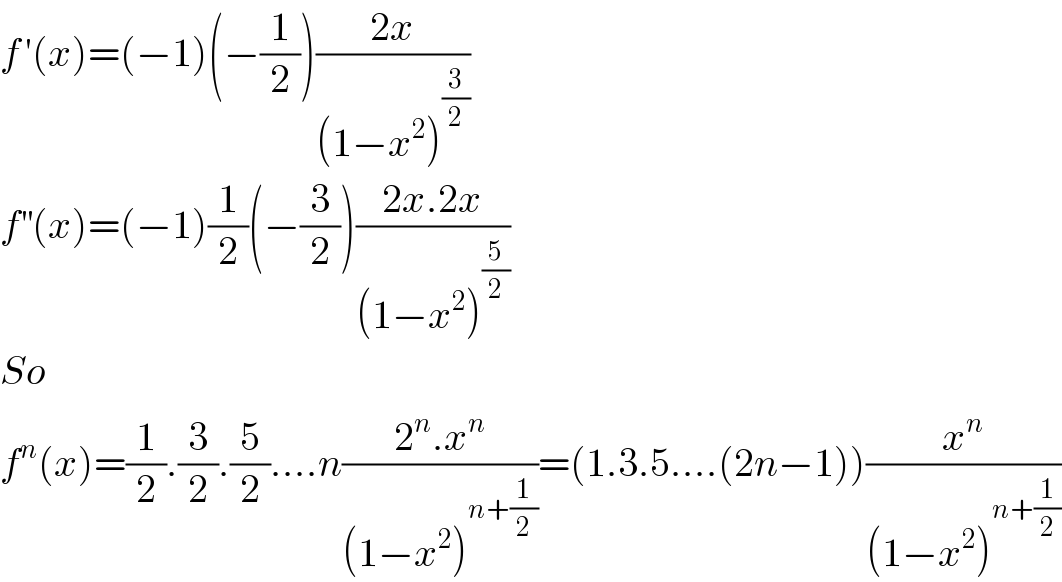
$${f}^{\:} '\left({x}\right)=\left(−\mathrm{1}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${f}^{''} \left({x}\right)=\left(−\mathrm{1}\right)\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)\frac{\mathrm{2}{x}.\mathrm{2}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{5}}{\mathrm{2}}} } \\ $$$${So} \\ $$$${f}^{{n}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{5}}{\mathrm{2}}….{n}\frac{\mathrm{2}^{{n}} .{x}^{{n}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} }=\left(\mathrm{1}.\mathrm{3}.\mathrm{5}….\left(\mathrm{2}{n}−\mathrm{1}\right)\right)\frac{{x}^{{n}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$
