Question Number 13281 by Tinkutara last updated on 17/May/17
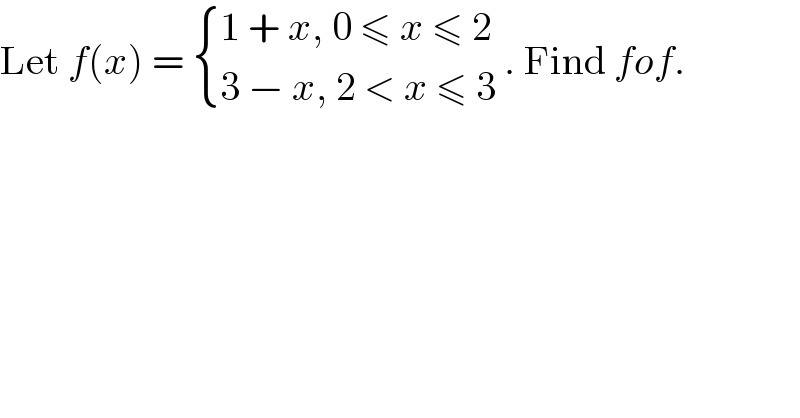
$$\mathrm{Let}\:{f}\left({x}\right)\:=\:\begin{cases}{\mathrm{1}\:+\:{x},\:\mathrm{0}\:\leqslant\:{x}\:\leqslant\:\mathrm{2}}\\{\mathrm{3}\:−\:{x},\:\mathrm{2}\:<\:{x}\:\leqslant\:\mathrm{3}}\end{cases}\:.\:\mathrm{Find}\:{fof}. \\ $$
Answered by ajfour last updated on 17/May/17

Commented by ajfour last updated on 17/May/17

Commented by ajfour last updated on 17/May/17
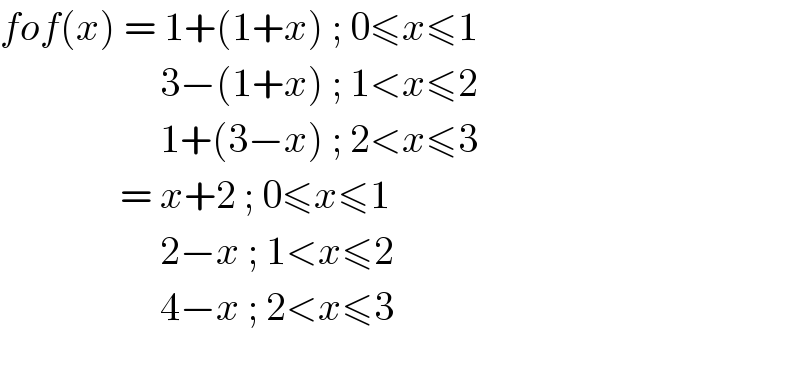
$${fof}\left({x}\right)\:=\:\mathrm{1}+\left(\mathrm{1}+{x}\right)\:;\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}−\left(\mathrm{1}+{x}\right)\:;\:\mathrm{1}<{x}\leqslant\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}+\left(\mathrm{3}−{x}\right)\:;\:\mathrm{2}<{x}\leqslant\mathrm{3}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{x}+\mathrm{2}\:;\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}−{x}\:;\:\mathrm{1}<{x}\leqslant\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}−{x}\:;\:\mathrm{2}<{x}\leqslant\mathrm{3} \\ $$$$ \\ $$
