Menu Close

let-f-x-1-x-2-1-let-U-n-f-n-x-prove-that-k-0-n-C-n-k-U-k-U-n-1-k-0-for-n-2-2-developp-f-at-integr-serie-

Tinku Tara 0 Comments
Pin




Question Number 60706 by maxmathsup by imad last updated on 24/May/19
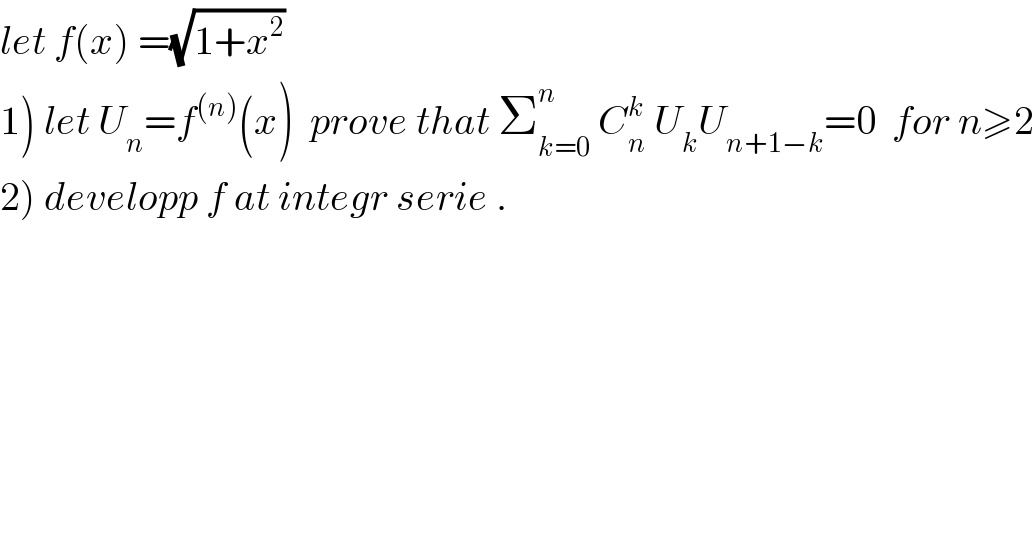
let f(x) =(√(1+x^2 )) 1) let U_n =f^((n)) (x) prove that Σ_(k=0) ^n C_n ^k U_k U_(n+1−k) =0 for n≥2 2) developp f at integr serie .
$${let}\:{f}\left({x}\right)\:=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\left.\mathrm{1}\right)\:{let}\:{U}_{{n}} ={f}^{\left({n}\right)} \left({x}\right)\:\:{prove}\:{that}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{U}_{{k}} {U}_{{n}+\mathrm{1}−{k}} =\mathrm{0}\:\:{for}\:{n}\geqslant\mathrm{2} \\ $$$$\left.\mathrm{2}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie}\:. \\ $$
Commented by maxmathsup by imad last updated on 03/Jun/19
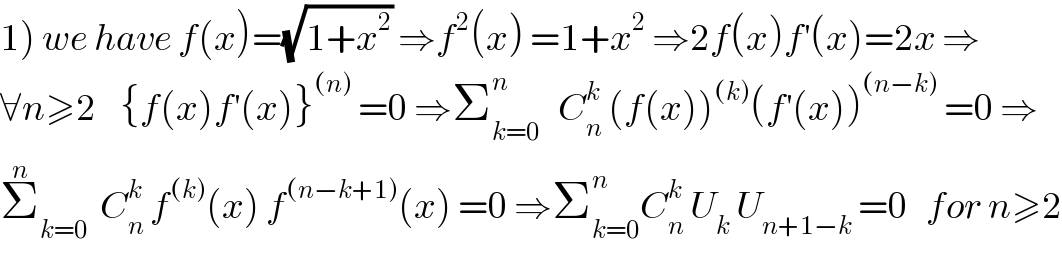
1) we have f(x)=(√(1+x^2 )) ⇒f^2 (x) =1+x^2 ⇒2f(x)f^′ (x)=2x ⇒ ∀n≥2 {f(x)f^′ (x)}^((n)) =0 ⇒Σ_(k=0) ^n C_n ^k (f(x))^((k)) (f^′ (x))^((n−k)) =0 ⇒ Σ_(k=0) ^n C_n ^k f^((k)) (x) f^((n−k+1)) (x) =0 ⇒Σ_(k=0) ^n C_n ^k U_k U_(n+1−k) =0 for n≥2
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x}\right)=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow{f}^{\mathrm{2}} \left({x}\right)\:=\mathrm{1}+{x}^{\mathrm{2}} \:\Rightarrow\mathrm{2}{f}\left({x}\right){f}^{'} \left({x}\right)=\mathrm{2}{x}\:\Rightarrow \\ $$$$\forall{n}\geqslant\mathrm{2}\:\:\:\:\left\{{f}\left({x}\right){f}^{'} \left({x}\right)\right\}^{\left({n}\right)} \:=\mathrm{0}\:\Rightarrow\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\:{C}_{{n}} ^{{k}} \:\left({f}\left({x}\right)\right)^{\left({k}\right)} \left({f}^{'} \left({x}\right)\right)^{\left({n}−{k}\right)} \:=\mathrm{0}\:\Rightarrow \\ $$$$\overset{{n}} {\sum}_{{k}=\mathrm{0}} \:\:{C}_{{n}} ^{{k}} \:{f}^{\left({k}\right)} \left({x}\right)\:{f}^{\left({n}−{k}+\mathrm{1}\right)} \left({x}\right)\:=\mathrm{0}\:\Rightarrow\sum_{{k}=\mathrm{0}} ^{{n}} {C}_{{n}} ^{{k}} \:{U}_{{k}} \:{U}_{{n}+\mathrm{1}−{k}} \:=\mathrm{0}\:\:\:{for}\:{n}\geqslant\mathrm{2} \\ $$
Commented by maxmathsup by imad last updated on 03/Jun/19
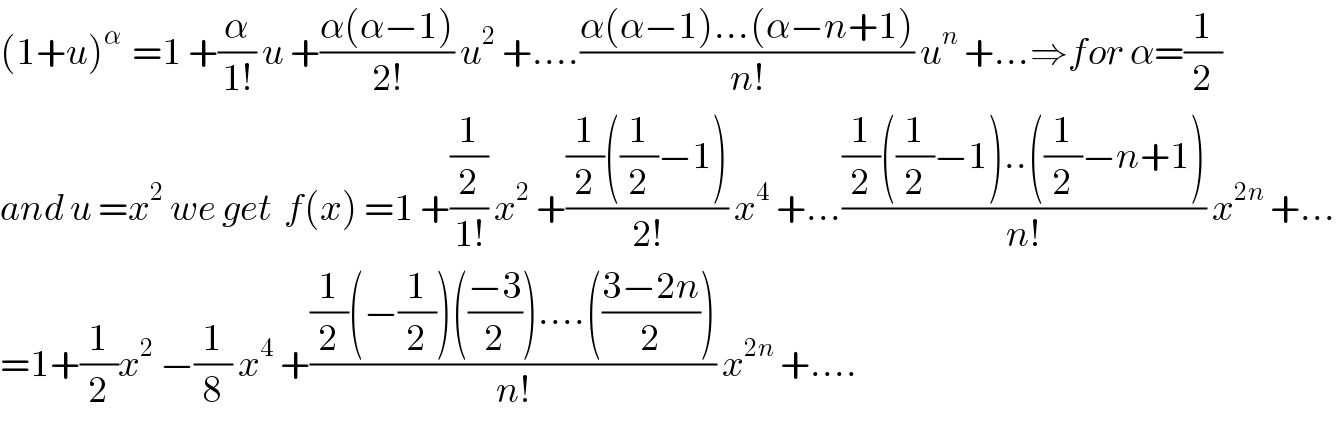
(1+u)^(α ) =1 +(α/(1!)) u +((α(α−1))/(2!)) u^2 +....((α(α−1)...(α−n+1))/(n!)) u^n +...⇒for α=(1/2) and u =x^2 we get f(x) =1 +((1/2)/(1!)) x^2 +(((1/2)((1/2)−1))/(2!)) x^4 +...(((1/2)((1/2)−1)..((1/2)−n+1))/(n!)) x^(2n) +... =1+(1/2)x^2 −(1/8) x^4 +(((1/2)(−(1/2))(((−3)/2))....(((3−2n)/2)))/(n!)) x^(2n) +....
$$\left(\mathrm{1}+{u}\right)^{\alpha\:} \:=\mathrm{1}\:+\frac{\alpha}{\mathrm{1}!}\:{u}\:+\frac{\alpha\left(\alpha−\mathrm{1}\right)}{\mathrm{2}!}\:{u}^{\mathrm{2}} \:+….\frac{\alpha\left(\alpha−\mathrm{1}\right)…\left(\alpha−{n}+\mathrm{1}\right)}{{n}!}\:{u}^{{n}} \:+…\Rightarrow{for}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${and}\:{u}\:={x}^{\mathrm{2}} \:{we}\:{get}\:\:{f}\left({x}\right)\:=\mathrm{1}\:+\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}!}\:{x}^{\mathrm{2}} \:+\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}!}\:{x}^{\mathrm{4}} \:+…\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)..\left(\frac{\mathrm{1}}{\mathrm{2}}−{n}+\mathrm{1}\right)}{{n}!}\:{x}^{\mathrm{2}{n}} \:+… \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \:−\frac{\mathrm{1}}{\mathrm{8}}\:{x}^{\mathrm{4}} \:+\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{−\mathrm{3}}{\mathrm{2}}\right)….\left(\frac{\mathrm{3}−\mathrm{2}{n}}{\mathrm{2}}\right)}{{n}!}\:{x}^{\mathrm{2}{n}} \:+…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *