Question Number 81165 by abdomathmax last updated on 09/Feb/20
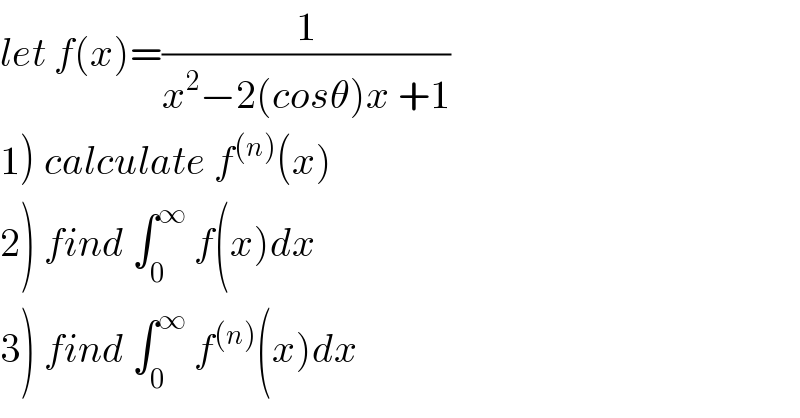
$${let}\:{f}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{2}\left({cos}\theta\right){x}\:+\mathrm{1}} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}^{\left({n}\right)} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:\int_{\mathrm{0}} ^{\infty} \:{f}\left({x}\right){dx} \\ $$$$\left.\mathrm{3}\right)\:{find}\:\int_{\mathrm{0}} ^{\infty} \:{f}^{\left({n}\right)} \left({x}\right){dx} \\ $$
Commented by mathmax by abdo last updated on 10/Feb/20
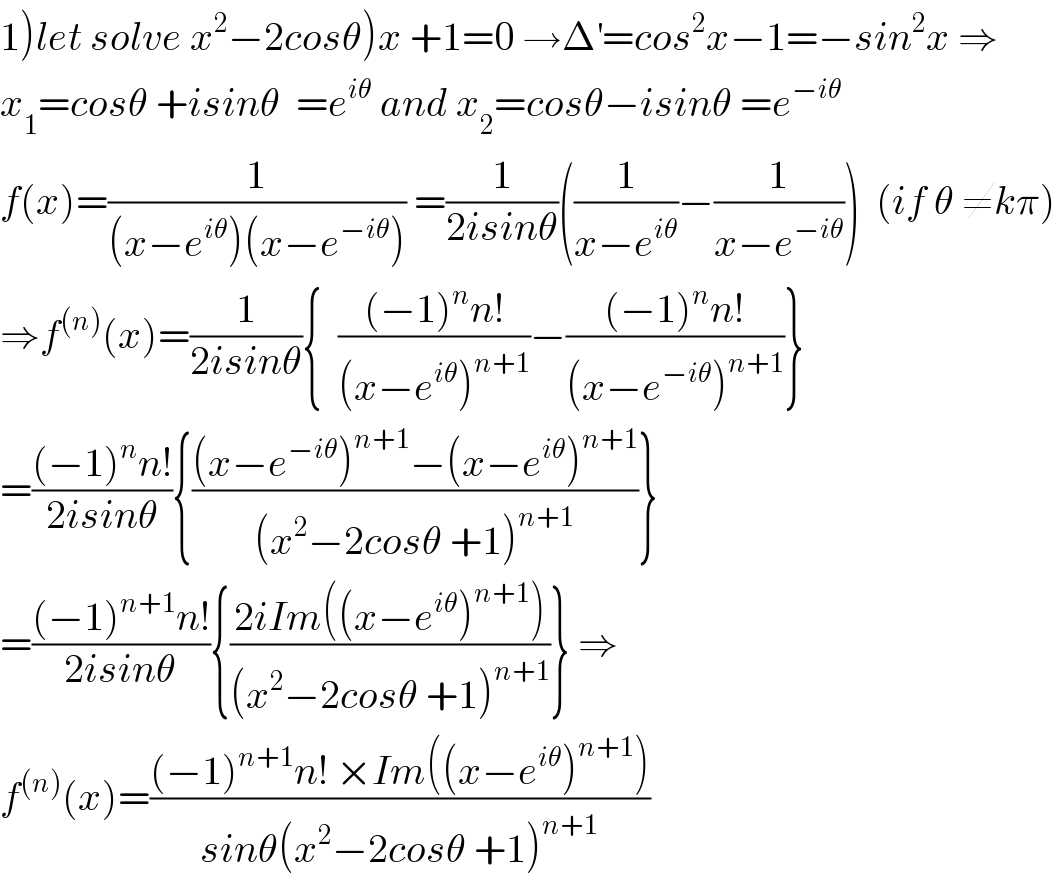
$$\left.\mathrm{1}\left.\right){let}\:{solve}\:{x}^{\mathrm{2}} −\mathrm{2}{cos}\theta\right){x}\:+\mathrm{1}=\mathrm{0}\:\rightarrow\Delta^{'} ={cos}^{\mathrm{2}} {x}−\mathrm{1}=−{sin}^{\mathrm{2}} {x}\:\Rightarrow \\ $$$${x}_{\mathrm{1}} ={cos}\theta\:+{isin}\theta\:\:={e}^{{i}\theta} \:{and}\:{x}_{\mathrm{2}} ={cos}\theta−{isin}\theta\:={e}^{−{i}\theta} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\left({x}−{e}^{{i}\theta} \right)\left({x}−{e}^{−{i}\theta} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}{isin}\theta}\left(\frac{\mathrm{1}}{{x}−{e}^{{i}\theta} }−\frac{\mathrm{1}}{{x}−{e}^{−{i}\theta} }\right)\:\:\left({if}\:\theta\:\neq{k}\pi\right) \\ $$$$\Rightarrow{f}^{\left({n}\right)} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}{isin}\theta}\left\{\:\:\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({x}−{e}^{{i}\theta} \right)^{{n}+\mathrm{1}} }−\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({x}−{e}^{−{i}\theta} \right)^{{n}+\mathrm{1}} }\right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\mathrm{2}{isin}\theta}\left\{\frac{\left({x}−{e}^{−{i}\theta} \right)^{{n}+\mathrm{1}} −\left({x}−{e}^{{i}\theta} \right)^{{n}+\mathrm{1}} }{\left({x}^{\mathrm{2}} −\mathrm{2}{cos}\theta\:+\mathrm{1}\right)^{{n}+\mathrm{1}} }\right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {n}!}{\mathrm{2}{isin}\theta}\left\{\frac{\mathrm{2}{iIm}\left(\left({x}−{e}^{{i}\theta} \right)^{{n}+\mathrm{1}} \right)}{\left({x}^{\mathrm{2}} −\mathrm{2}{cos}\theta\:+\mathrm{1}\right)^{{n}+\mathrm{1}} }\right\}\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {n}!\:×{Im}\left(\left({x}−{e}^{{i}\theta} \right)^{{n}+\mathrm{1}} \right)}{{sin}\theta\left({x}^{\mathrm{2}} −\mathrm{2}{cos}\theta\:+\mathrm{1}\right)^{{n}+\mathrm{1}} } \\ $$
Commented by mathmax by abdo last updated on 10/Feb/20

$$\left.\mathrm{2}\right)\:{if}\:\theta={k}\pi\:\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{\left({x}\overset{−} {+}\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\int\:{f}\left({x}\right){dx}=−\frac{\mathrm{1}}{{x}\overset{−} {+}\mathrm{1}}\:+{c} \\ $$$${if}\:\theta\neq{k}\pi\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:{f}\left({x}\right){dx}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}{cos}\theta\:{x}\:+{cos}^{\mathrm{2}} \theta\:+{sin}^{\mathrm{2}} \theta} \\ $$
Commented by mathmax by abdo last updated on 10/Feb/20
![∫_0 ^∞ f(x)dx=∫_0 ^∞ (dx/((x−cosθ)^2 +sin^2 θ)) =_(x−cosθ =∣sinθ∣u) ∫_(−((cosθ)/(∣sinθ∣))) ^(+∞) (1/(sin^2 θ(1+u^2 )))∣sinθ∣ du =(1/(∣sinθ∣)) [arctanu]_(−((cosθ)/(∣sinθ∣))) ^(+∞) =(1/(∣sinθ∣)){(π/2) +arctan(((cosθ)/(∣sinθ∣)))} ⇒ if sinθ>0 ⇒∫_0 ^∞ f(x)dx=(1/(sinθ)){(π/2) +arctan((1/(tanθ)))} =(1/(sinθ)){π−θ} if sinθ<0 ⇒∫_0 ^∞ f(xdx=−(1/(sinθ)){(π/2)−arctan((1/(tanθ)))} =−(1/(sinθ)){(π/2)−(−(π/2) −θ)} =−(1/(sinθ)){π +θ}](https://www.tinkutara.com/question/Q81210.png)
$$\int_{\mathrm{0}} ^{\infty} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}−{cos}\theta\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} \theta} \\ $$$$=_{{x}−{cos}\theta\:=\mid{sin}\theta\mid{u}} \:\:\:\:\int_{−\frac{{cos}\theta}{\mid{sin}\theta\mid}} ^{+\infty} \:\:\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \theta\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\mid{sin}\theta\mid\:{du} \\ $$$$=\frac{\mathrm{1}}{\mid{sin}\theta\mid}\:\left[{arctanu}\right]_{−\frac{{cos}\theta}{\mid{sin}\theta\mid}} ^{+\infty} \:=\frac{\mathrm{1}}{\mid{sin}\theta\mid}\left\{\frac{\pi}{\mathrm{2}}\:+{arctan}\left(\frac{{cos}\theta}{\mid{sin}\theta\mid}\right)\right\}\:\Rightarrow \\ $$$${if}\:{sin}\theta>\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} {f}\left({x}\right){dx}=\frac{\mathrm{1}}{{sin}\theta}\left\{\frac{\pi}{\mathrm{2}}\:+{arctan}\left(\frac{\mathrm{1}}{{tan}\theta}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{{sin}\theta}\left\{\pi−\theta\right\} \\ $$$${if}\:{sin}\theta<\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} {f}\left({xdx}=−\frac{\mathrm{1}}{{sin}\theta}\left\{\frac{\pi}{\mathrm{2}}−{arctan}\left(\frac{\mathrm{1}}{{tan}\theta}\right)\right\}\right. \\ $$$$=−\frac{\mathrm{1}}{{sin}\theta}\left\{\frac{\pi}{\mathrm{2}}−\left(−\frac{\pi}{\mathrm{2}}\:−\theta\right)\right\}\:=−\frac{\mathrm{1}}{{sin}\theta}\left\{\pi\:+\theta\right\} \\ $$
Answered by mind is power last updated on 09/Feb/20
![x^2 −2cos(θ)x+1=(x−e^(iθ) )(x−e^(−iθ) ) f(x)=(1/(2isin(θ))).(1/(x−e^(iθ) ))−(1/(2isin(θ))).(1/(x−e^(−iθ) )) f(x)=2Re((1/(2i.sin(θ)(x−e^(iθ) )))) g(x)=(1/(x−e^(iθ) )).(1/(2isin(θ))) f^n =2Re(g^n (x)) g^n (x)=(((−1)^n n!.)/((x−e^(iθ) )^(n+1) )).(1/(2isin(θ))) f(x)=2Re((((−1)^n n!)/((x−e^(iθ) )^(n+1) )).(1/(2isin(θ)))) =(−1)^n n! Re{(((x−e^(−iθ) )^(n+1) )/((x^2 −2cos(θ)x+1)^(n+1) )).(1/(2isin(θ)))} x−e^(−iθ) =x−cos(θ)+isin(θ) =(√(x^2 −2cos(θ)x+1)).(((x−cos(θ))/( (√(x^2 −2xcos(θ)+1))))+((isin(θ))/( (√(x^2 −2xcos(θ)+1))))) =(√(x^2 −2cos(θ)x+1)).e^(i(kπ+arctan(((sin(θ))/(x−cos(θ)))))) ,k∈{−1,0,1} =(−1)^n n!((sin((n+1){kπ+arctan(((sin(θ))/(x−sin(θ))))}))/((x^2 −2xcos(θ)+1)^((n+1)/2) sin(θ))) may bee error of calculus 2)(x^2 −2cos(θ)x+1)=(x−cos(θ))^2 +sin^2 (θ) =sin^2 (θ)(((x/(sin(θ)))−cot(θ))^2 +1) ∫(dx/((x^2 −2cos(θ)x+1)))=∫(dx/(sin^2 (θ)(((x/(sin(θ)))−cot(θ))^2 +1))) ∀θ∈]0,2π[ ∣sin(θ)≠0 if sin(θ)=0⇒cos(θ)∈{−1,1} since f(−x)=x^2 −2xcos(θ)+1⇒cos(θ)=1 is ennough to find f(x), ⇒f(x)=(1/((x−1)^2 )) not integrable over IR_+ ⇒θ≠0 θ=π⇒f(x)=(1/((x+1)^2 )) ⇒∫_0 ^(+∞) (dx/((1+x)^2 ))=1 ∀θ∈[0,2π[−{0,π} f(x)=(1/(sin^2 (θ){((x/(sin(θ)))−cot(θ))^2 +1})) ∫_0 ^(+∞) f(x)dx=(1/(sin(θ)))[arctan((x/(sin(θ)))−cot(θ))]_0 ^(+∞) if θ∈]0,π[ f(x)=(1/(sin(θ))){(π/2)+arctan(cot(θ))} =(1/(sin(θ))){π−θ} if θ∈]π,2π[ f(x)=(1/(sin(θ))){−(π/2)+arctan(cot(θ))} =(1/(sin(θ))){−(π/2)+arctan(cot(π+(θ−π))} =(1/(sin(θ))){−(π/2)+arctan(cot(θ−π))}=(1/(sin(θ))){−(π/2)+arctan(tan(((3π)/2)−θ)) =(1/(sin(θ))){−(π/2)+((3π)/2)−θ}=(1/(sin(θ)))(π−θ) ⇒∫_0 ^(+∞) f(x)dx=((π−θ)/(sin(θ))),θ∈[0,2π]−{0,π} θ=π⇒f(x)=1 we can see that lim_(x→π) ((π−θ)/(sin(θ)))=−(1/(cos(π)))=1 3 ∀n≥2 =lim_(x→∞) f^(n−1) (x)−f^(n−1) (0)](https://www.tinkutara.com/question/Q81167.png)
$${x}^{\mathrm{2}} −\mathrm{2}{cos}\left(\theta\right){x}+\mathrm{1}=\left({x}−{e}^{{i}\theta} \right)\left({x}−{e}^{−{i}\theta} \right) \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}{isin}\left(\theta\right)}.\frac{\mathrm{1}}{{x}−{e}^{{i}\theta} }−\frac{\mathrm{1}}{\mathrm{2}{isin}\left(\theta\right)}.\frac{\mathrm{1}}{{x}−{e}^{−{i}\theta} } \\ $$$${f}\left({x}\right)=\mathrm{2}{Re}\left(\frac{\mathrm{1}}{\mathrm{2}{i}.{sin}\left(\theta\right)\left({x}−{e}^{{i}\theta} \right)}\right) \\ $$$${g}\left({x}\right)=\frac{\mathrm{1}}{{x}−{e}^{{i}\theta} }.\frac{\mathrm{1}}{\mathrm{2}{isin}\left(\theta\right)} \\ $$$${f}^{{n}} =\mathrm{2}{Re}\left({g}^{{n}} \left({x}\right)\right) \\ $$$${g}^{{n}} \left({x}\right)=\frac{\left(−\mathrm{1}\right)^{{n}} {n}!.}{\left({x}−{e}^{{i}\theta} \right)^{{n}+\mathrm{1}} }.\frac{\mathrm{1}}{\mathrm{2}{isin}\left(\theta\right)} \\ $$$${f}\left({x}\right)=\mathrm{2}{Re}\left(\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({x}−{e}^{{i}\theta} \right)^{{n}+\mathrm{1}} }.\frac{\mathrm{1}}{\mathrm{2}{isin}\left(\theta\right)}\right) \\ $$$$=\left(−\mathrm{1}\right)^{{n}} {n}!\:{Re}\left\{\frac{\left({x}−{e}^{−{i}\theta} \right)^{{n}+\mathrm{1}} }{\left({x}^{\mathrm{2}} −\mathrm{2}{cos}\left(\theta\right){x}+\mathrm{1}\right)^{{n}+\mathrm{1}} }.\frac{\mathrm{1}}{\mathrm{2}{isin}\left(\theta\right)}\right\} \\ $$$${x}−{e}^{−{i}\theta} \\ $$$$={x}−{cos}\left(\theta\right)+{isin}\left(\theta\right) \\ $$$$=\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{cos}\left(\theta\right){x}+\mathrm{1}}.\left(\frac{{x}−{cos}\left(\theta\right)}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{xcos}\left(\theta\right)+\mathrm{1}}}+\frac{{isin}\left(\theta\right)}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{xcos}\left(\theta\right)+\mathrm{1}}}\right) \\ $$$$ \\ $$$$=\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{cos}\left(\theta\right){x}+\mathrm{1}}.{e}^{{i}\left({k}\pi+{arctan}\left(\frac{{sin}\left(\theta\right)}{{x}−{cos}\left(\theta\right)}\right)\right)} ,{k}\in\left\{−\mathrm{1},\mathrm{0},\mathrm{1}\right\} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} {n}!\frac{{sin}\left(\left({n}+\mathrm{1}\right)\left\{{k}\pi+{arctan}\left(\frac{{sin}\left(\theta\right)}{{x}−{sin}\left(\theta\right)}\right)\right\}\right)}{\left({x}^{\mathrm{2}} −\mathrm{2}{xcos}\left(\theta\right)+\mathrm{1}\right)^{\frac{{n}+\mathrm{1}}{\mathrm{2}}} {sin}\left(\theta\right)} \\ $$$${may}\:{bee}\:{error}\:{of}\:{calculus} \\ $$$$\left.\mathrm{2}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{cos}\left(\theta\right){x}+\mathrm{1}\right)=\left({x}−{cos}\left(\theta\right)\right)^{\mathrm{2}} +{sin}^{\mathrm{2}} \left(\theta\right) \\ $$$$={sin}^{\mathrm{2}} \left(\theta\right)\left(\left(\frac{{x}}{{sin}\left(\theta\right)}−{cot}\left(\theta\right)\right)^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} −\mathrm{2}{cos}\left(\theta\right){x}+\mathrm{1}\right)}=\int\frac{{dx}}{{sin}^{\mathrm{2}} \left(\theta\right)\left(\left(\frac{{x}}{{sin}\left(\theta\right)}−{cot}\left(\theta\right)\right)^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\left.\forall\theta\in\right]\mathrm{0},\mathrm{2}\pi\left[\:\mid{sin}\left(\theta\right)\neq\mathrm{0}\right. \\ $$$${if}\:{sin}\left(\theta\right)=\mathrm{0}\Rightarrow{cos}\left(\theta\right)\in\left\{−\mathrm{1},\mathrm{1}\right\} \\ $$$${since}\:{f}\left(−{x}\right)={x}^{\mathrm{2}} −\mathrm{2}{xcos}\left(\theta\right)+\mathrm{1}\Rightarrow{cos}\left(\theta\right)=\mathrm{1}\:{is}\:{ennough} \\ $$$${to}\:{find}\:{f}\left({x}\right), \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:{not}\:{integrable}\:{over}\:{IR}_{+} \\ $$$$\Rightarrow\theta\neq\mathrm{0} \\ $$$$\theta=\pi\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{+\infty} \frac{{dx}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }=\mathrm{1} \\ $$$$\forall\theta\in\left[\mathrm{0},\mathrm{2}\pi\left[−\left\{\mathrm{0},\pi\right\}\right.\right. \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \left(\theta\right)\left\{\left(\frac{{x}}{{sin}\left(\theta\right)}−{cot}\left(\theta\right)\right)^{\mathrm{2}} +\mathrm{1}\right\}} \\ $$$$\int_{\mathrm{0}} ^{+\infty} {f}\left({x}\right){dx}=\frac{\mathrm{1}}{{sin}\left(\theta\right)}\left[{arctan}\left(\frac{{x}}{{sin}\left(\theta\right)}−{cot}\left(\theta\right)\right)\right]_{\mathrm{0}} ^{+\infty} \\ $$$$\left.{if}\:\theta\in\right]\mathrm{0},\pi\left[\right. \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{sin}\left(\theta\right)}\left\{\frac{\pi}{\mathrm{2}}+{arctan}\left({cot}\left(\theta\right)\right)\right\} \\ $$$$=\frac{\mathrm{1}}{{sin}\left(\theta\right)}\left\{\pi−\theta\right\} \\ $$$$\left.{if}\:\theta\in\right]\pi,\mathrm{2}\pi\left[\right. \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{sin}\left(\theta\right)}\left\{−\frac{\pi}{\mathrm{2}}+{arctan}\left({cot}\left(\theta\right)\right)\right\} \\ $$$$=\frac{\mathrm{1}}{{sin}\left(\theta\right)}\left\{−\frac{\pi}{\mathrm{2}}+{arctan}\left({cot}\left(\pi+\left(\theta−\pi\right)\right)\right\}\right. \\ $$$$=\frac{\mathrm{1}}{{sin}\left(\theta\right)}\left\{−\frac{\pi}{\mathrm{2}}+{arctan}\left({cot}\left(\theta−\pi\right)\right)\right\}=\frac{\mathrm{1}}{{sin}\left(\theta\right)}\left\{−\frac{\pi}{\mathrm{2}}+{arctan}\left({tan}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}−\theta\right)\right)\right. \\ $$$$=\frac{\mathrm{1}}{{sin}\left(\theta\right)}\left\{−\frac{\pi}{\mathrm{2}}+\frac{\mathrm{3}\pi}{\mathrm{2}}−\theta\right\}=\frac{\mathrm{1}}{{sin}\left(\theta\right)}\left(\pi−\theta\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{+\infty} {f}\left({x}\right){dx}=\frac{\pi−\theta}{{sin}\left(\theta\right)},\theta\in\left[\mathrm{0},\mathrm{2}\pi\right]−\left\{\mathrm{0},\pi\right\} \\ $$$$\theta=\pi\Rightarrow{f}\left({x}\right)=\mathrm{1}\:\:{we}\:{can}\:{see}\:{that} \\ $$$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{\pi−\theta}{{sin}\left(\theta\right)}=−\frac{\mathrm{1}}{{cos}\left(\pi\right)}=\mathrm{1}\:\:\: \\ $$$$\mathrm{3}\:\forall{n}\geqslant\mathrm{2}\:=\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}^{{n}−\mathrm{1}} \left({x}\right)−{f}^{{n}−\mathrm{1}} \left(\mathrm{0}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 10/Feb/20

$${thank}\:{you}\:{sir}. \\ $$
Commented by mind is power last updated on 10/Feb/20

$${withe}\:{pleasur}\:{sir} \\ $$
