Question Number 30595 by abdo imad last updated on 23/Feb/18
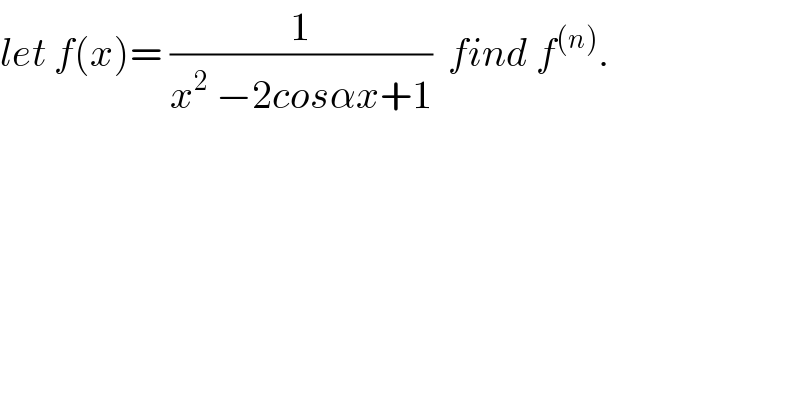
$${let}\:{f}\left({x}\right)=\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:−\mathrm{2}{cos}\alpha{x}+\mathrm{1}}\:\:{find}\:{f}^{\left({n}\right)} . \\ $$
Commented by abdo imad last updated on 24/Feb/18

$${roots}\:{of}\:{p}\left({x}\right)={x}^{\mathrm{2}} \:−\mathrm{2}{cos}\alpha\:{x}\:+\mathrm{1}=\mathrm{0} \\ $$$$\Delta^{,} =\left(−{cos}\alpha\right)^{\mathrm{2}} −\mathrm{1}=−{sin}^{\mathrm{2}} \alpha=\left({isin}\alpha\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${z}_{\mathrm{1}} ={cos}\alpha\:+{isin}\alpha\:={e}^{{i}\alpha} \:\:{and}\:{z}_{\mathrm{2}} ={cos}\alpha\:−{isin}\alpha\:={e}^{−{i}\alpha} \Rightarrow \\ $$$${f}\left({x}\right)=\:\:\frac{\mathrm{1}}{\left({x}−{e}^{{i}\alpha} \right)\left({x}−{e}^{−{i}\alpha} \right)}=\:\frac{{a}}{{x}−{e}^{{i}\alpha} }\:\:+\:\frac{{b}}{{x}−{e}^{−{i}\alpha} } \\ $$$${a}={lim}_{{x}\rightarrow{e}^{{i}\alpha} } \:\:\left({x}−{e}^{{i}\alpha} \right){f}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}{isin}\left(\alpha\right)} \\ $$$${b}={lim}_{{x}\rightarrow{e}^{−{i}\alpha} } \:\left({x}−{e}^{−{i}\alpha} \right){f}\left({x}\right)=\frac{−\mathrm{1}}{\mathrm{2}{i}\:{sin}\alpha}\:\Rightarrow \\ $$$${f}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}{isin}\alpha}\left(\:\:\frac{\mathrm{1}}{{x}−{e}^{{i}\alpha} }\:−\:\frac{\mathrm{1}}{{x}−{e}^{−{i}\alpha} }\right)\Rightarrow \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}{isin}\alpha}\left(\:\left(\frac{\mathrm{1}}{{x}−{e}^{{i}\alpha} }\right)^{\left({n}\right)} \:−\left(\frac{\mathrm{1}}{{x}−{e}^{−{i}\alpha} }\:\right)^{\left({n}\right)} \right) \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}{isin}\alpha}\left(\:\:\frac{\left(−\mathrm{1}\right)^{{n}} \:{n}!}{\left({x}−{e}^{{i}\alpha} \right)^{{n}+\mathrm{1}} }\:−\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({x}−{e}^{−{i}\alpha} \right)^{{n}+\mathrm{1}} }\right) \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\mathrm{2}{isin}\alpha}\left(\:\:\frac{\left({x}−{e}^{−{i}\alpha} \right)^{{n}+\mathrm{1}} \:−\left({x}\:−{e}^{{i}\alpha} \right)^{{n}+\mathrm{1}} }{\left({x}^{\mathrm{2}} \:−\mathrm{2}{cos}\alpha{x}\:+\mathrm{1}\right)^{\mathrm{2}} }\right)\:{for}\:\alpha\neq{k}\pi \\ $$$${if}\:\alpha={k}\pi\:{f}\left({x}\right)=\:\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:{or}\:{f}\left({x}\right)=\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:{let}\:{find}\:{f}^{\left({n}\right)} \\ $$$${in}\:{case}\:{f}\left({x}\right)=\:\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{we}\:{have}\:{f}^{\left(\mathrm{1}\right)} \left({x}\right)=\frac{−\mathrm{2}\left({x}+\mathrm{1}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{4}} }=\frac{−\mathrm{2}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${f}^{\left(\mathrm{2}\right)} \left({x}\right)\:=\frac{\mathrm{3}×\mathrm{2}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\left({x}+\mathrm{1}\right)^{\mathrm{6}} }=\frac{\mathrm{3}×\mathrm{2}}{\left({x}+\mathrm{1}\right)^{\mathrm{4}} }\:{let}\:{suppose} \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\:\frac{\left({n}+\mathrm{1}\right)!\left(−\mathrm{1}\right)^{{n}} }{\left({x}+\mathrm{1}\right)^{{n}+\mathrm{2}} }\:\Rightarrow{f}^{\left({n}+\mathrm{1}\right)} \left({x}\right)=\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \left({n}+\mathrm{1}\right)!\left({n}+\mathrm{2}\right)\left({x}+\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({x}+\mathrm{1}\right)^{\mathrm{2}{n}+\mathrm{4}} } \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \left({n}+\mathrm{2}\right)!}{\left({x}+\mathrm{1}\right)^{{n}+\mathrm{3}} }\:\Rightarrow\:{f}^{\left({n}\right)} \left({x}\right)=\frac{\left(−\mathrm{1}\right)^{{n}} \left({n}+\mathrm{1}\right)!}{\left({x}+\mathrm{1}\right)^{{n}+\mathrm{2}} }\:. \\ $$
