Question Number 55269 by maxmathsup by imad last updated on 20/Feb/19
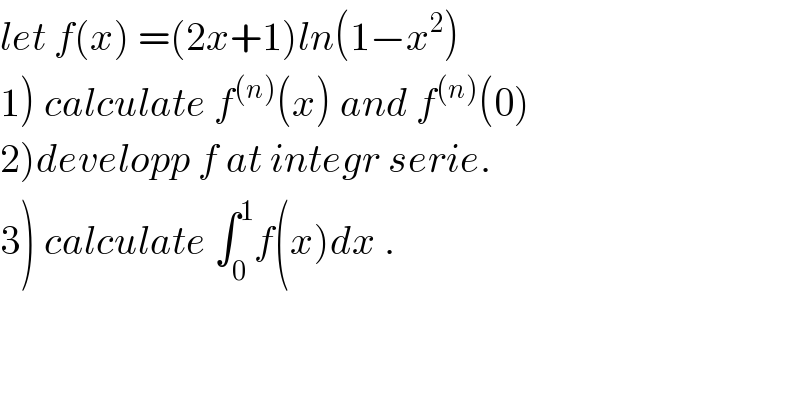
Commented by turbo msup by abdo last updated on 02/Mar/19
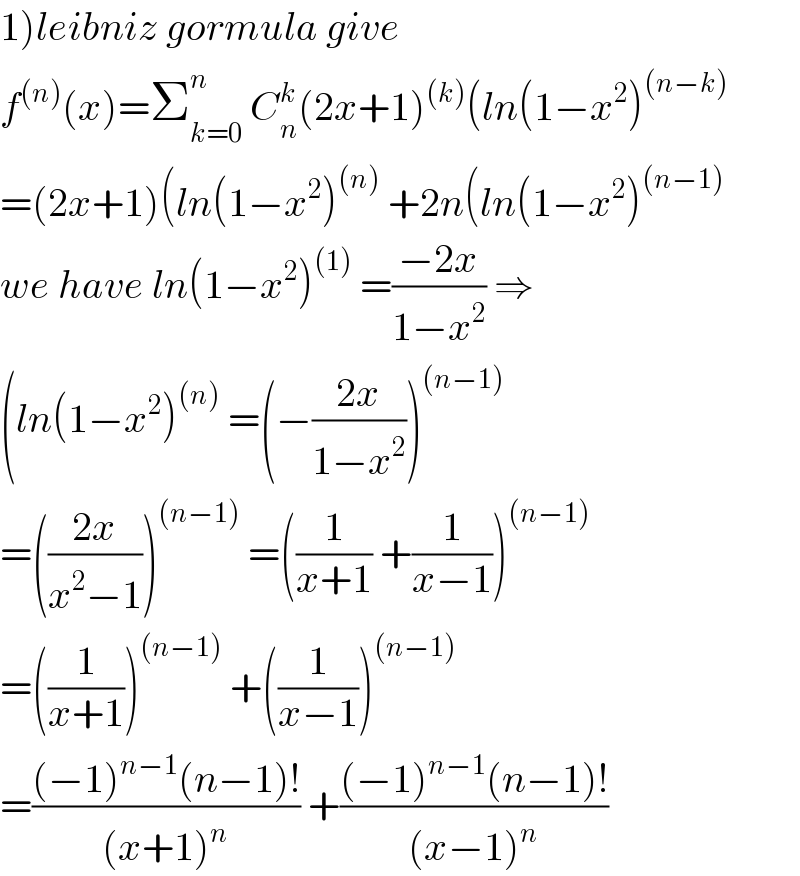
Commented by turbo msup by abdo last updated on 02/Mar/19
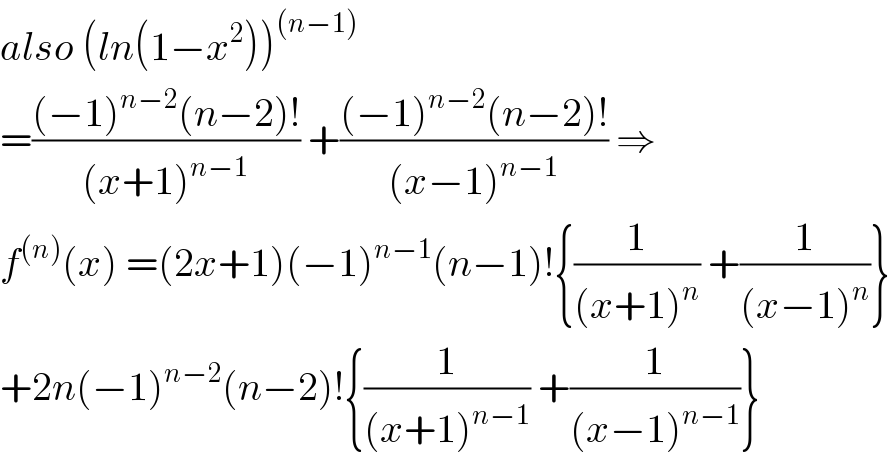
Commented by maxmathsup by imad last updated on 02/Mar/19
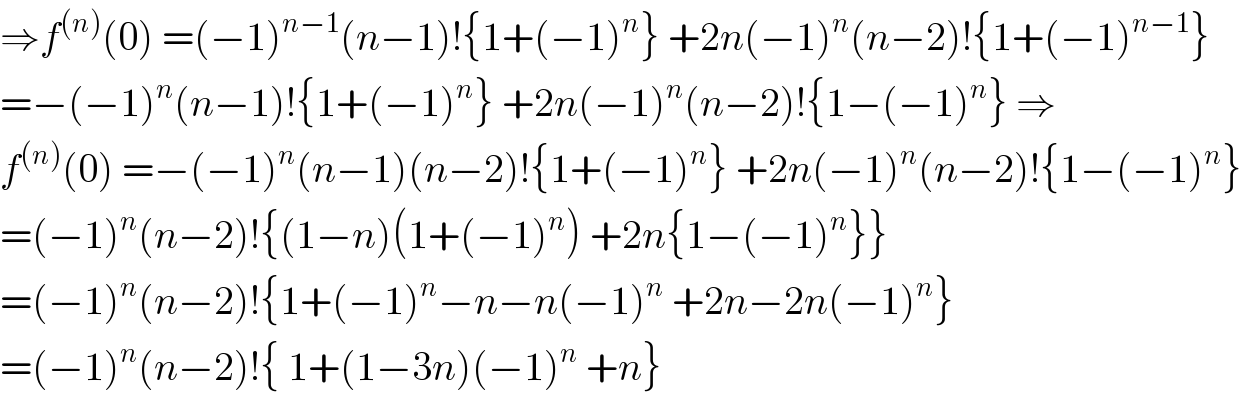
Commented by maxmathsup by imad last updated on 02/Mar/19

