Question Number 169922 by cortano1 last updated on 12/May/22
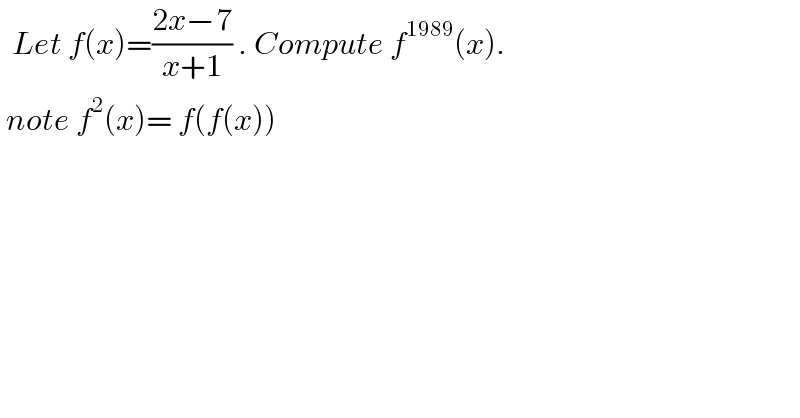
$$\:\:{Let}\:{f}\left({x}\right)=\frac{\mathrm{2}{x}−\mathrm{7}}{{x}+\mathrm{1}}\:.\:{Compute}\:{f}^{\mathrm{1989}} \left({x}\right). \\ $$$$\:{note}\:{f}^{\mathrm{2}} \left({x}\right)=\:{f}\left({f}\left({x}\right)\right) \\ $$
Answered by floor(10²Eta[1]) last updated on 12/May/22
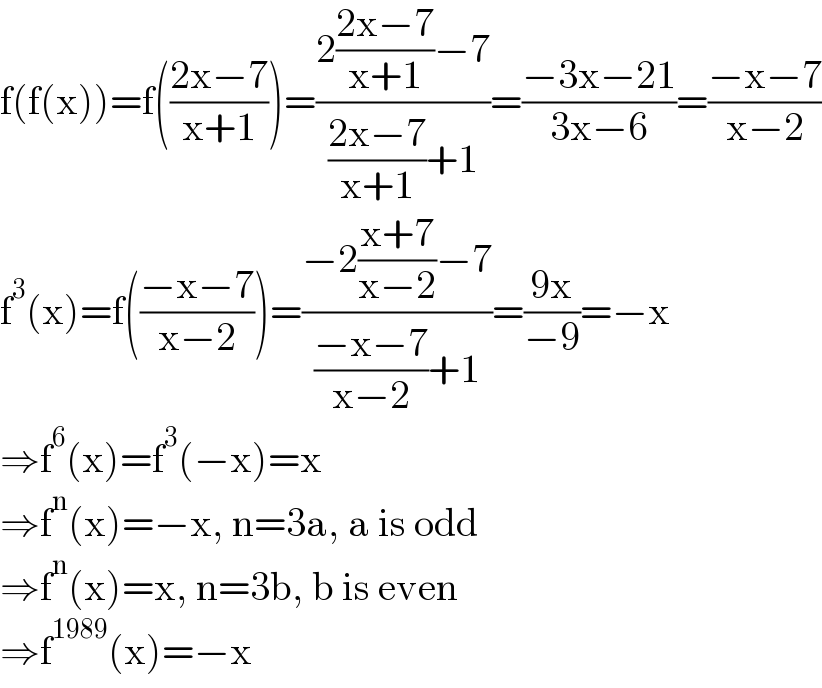
$$\mathrm{f}\left(\mathrm{f}\left(\mathrm{x}\right)\right)=\mathrm{f}\left(\frac{\mathrm{2x}−\mathrm{7}}{\mathrm{x}+\mathrm{1}}\right)=\frac{\mathrm{2}\frac{\mathrm{2x}−\mathrm{7}}{\mathrm{x}+\mathrm{1}}−\mathrm{7}}{\frac{\mathrm{2x}−\mathrm{7}}{\mathrm{x}+\mathrm{1}}+\mathrm{1}}=\frac{−\mathrm{3x}−\mathrm{21}}{\mathrm{3x}−\mathrm{6}}=\frac{−\mathrm{x}−\mathrm{7}}{\mathrm{x}−\mathrm{2}} \\ $$$$\mathrm{f}^{\mathrm{3}} \left(\mathrm{x}\right)=\mathrm{f}\left(\frac{−\mathrm{x}−\mathrm{7}}{\mathrm{x}−\mathrm{2}}\right)=\frac{−\mathrm{2}\frac{\mathrm{x}+\mathrm{7}}{\mathrm{x}−\mathrm{2}}−\mathrm{7}}{\frac{−\mathrm{x}−\mathrm{7}}{\mathrm{x}−\mathrm{2}}+\mathrm{1}}=\frac{\mathrm{9x}}{−\mathrm{9}}=−\mathrm{x} \\ $$$$\Rightarrow\mathrm{f}^{\mathrm{6}} \left(\mathrm{x}\right)=\mathrm{f}^{\mathrm{3}} \left(−\mathrm{x}\right)=\mathrm{x} \\ $$$$\Rightarrow\mathrm{f}^{\mathrm{n}} \left(\mathrm{x}\right)=−\mathrm{x},\:\mathrm{n}=\mathrm{3a},\:\mathrm{a}\:\mathrm{is}\:\mathrm{odd} \\ $$$$\Rightarrow\mathrm{f}^{\mathrm{n}} \left(\mathrm{x}\right)=\mathrm{x},\:\mathrm{n}=\mathrm{3b},\:\mathrm{b}\:\mathrm{is}\:\mathrm{even} \\ $$$$\Rightarrow\mathrm{f}^{\mathrm{1989}} \left(\mathrm{x}\right)=−\mathrm{x} \\ $$
