Question Number 41136 by math khazana by abdo last updated on 02/Aug/18
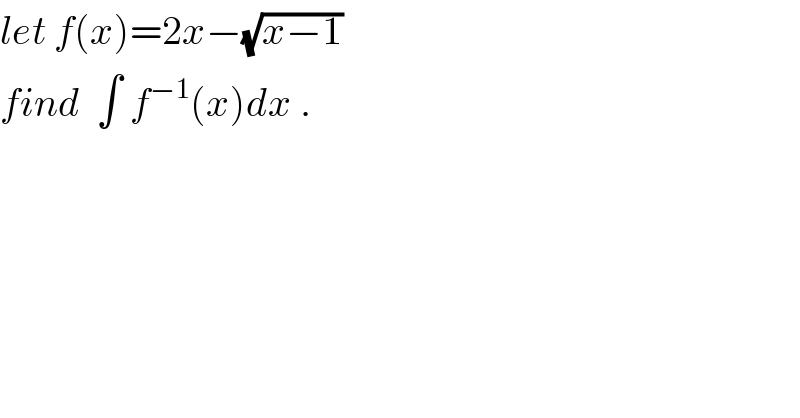
$${let}\:{f}\left({x}\right)=\mathrm{2}{x}−\sqrt{{x}−\mathrm{1}} \\ $$$${find}\:\:\int\:{f}^{−\mathrm{1}} \left({x}\right){dx}\:. \\ $$
Answered by MJS last updated on 02/Aug/18
![f(x) defined for x∈[1; +∞] f′(x)=2−(1/(2(√(x−1))))=0 ⇒ x=((17)/(16)) f′′(x)=(1/(4(x−1)^(3/2) )); f′′(((17)/(16)))=16>0 ⇒ min at ((((17)/(16))),(((15)/8)) ) range(f(x))=[((15)/8); +∞[ x=2y−(√(y−1)) (√(y−1))=2y−x y−1=4y^2 −4xy+x^2 y^2 −(x+(1/4))y+((x^2 +1)/4)=0 y_1 =(x/2)+(1/8)−((√(8x−15))/8) defined for x∈[((15)/8); +∞] y_1 ′=(1/2)−(1/(2(√(8x−15))))=0 ⇒ x=2 y_1 ′′=(2/((8x−15)^(3/2) )); x=2 ⇒ y_2 ′′=2>0 ⇒ min at ((2),(1) ) range=[1; +∞] y_2 =(x/2)+(1/8)+((√(8x−15))/8) defined for x∈[((15)/8); +∞] y_2 ′=(1/2)+(1/(2(√(8x−15))))=0 ⇒ no solution range=[((17)/(16)); +∞] f^(−1) (x)= { (((x/2)+(1/8)−((√(8x−15))/8); x∈[((15)/8); 2])),(((x/2)+(1/8)+((√(8x−15))/8); x∈]((15)/8); +∞[)) :} ∫f^(−1) (x)dx= { (((x^2 /4)+(x/8)−(((8x−15)^(3/2) )/(96)); x∈[((15)/8); 2])),(((x^2 /4)+(x/8)+(((8x−15)^(3/2) )/(96)); x∈]((15)/8); +∞[)) :} but of course if you want the area between this function and the x−axis you must take ∫f^(−1) (x)dx= { (((x^2 /4)+(x/8)−(((8x−15)^(3/2) )/(96)); x∈[((15)/8); 2])),(((x^2 /4)+(x/8)+(((8x−15)^(3/2) )/(96)); x∈]2; +∞[)) :}](https://www.tinkutara.com/question/Q41161.png)
$${f}\left({x}\right)\:\mathrm{defined}\:\mathrm{for}\:{x}\in\left[\mathrm{1};\:+\infty\right] \\ $$$${f}'\left({x}\right)=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}−\mathrm{1}}}=\mathrm{0}\:\Rightarrow\:{x}=\frac{\mathrm{17}}{\mathrm{16}} \\ $$$${f}''\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}\left({x}−\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} };\:{f}''\left(\frac{\mathrm{17}}{\mathrm{16}}\right)=\mathrm{16}>\mathrm{0}\:\Rightarrow\:\mathrm{min}\:\mathrm{at}\:\begin{pmatrix}{\frac{\mathrm{17}}{\mathrm{16}}}\\{\frac{\mathrm{15}}{\mathrm{8}}}\end{pmatrix} \\ $$$$\mathrm{range}\left({f}\left({x}\right)\right)=\left[\frac{\mathrm{15}}{\mathrm{8}};\:+\infty\left[\right.\right. \\ $$$${x}=\mathrm{2}{y}−\sqrt{{y}−\mathrm{1}} \\ $$$$\sqrt{{y}−\mathrm{1}}=\mathrm{2}{y}−{x} \\ $$$${y}−\mathrm{1}=\mathrm{4}{y}^{\mathrm{2}} −\mathrm{4}{xy}+{x}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} −\left({x}+\frac{\mathrm{1}}{\mathrm{4}}\right){y}+\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$${y}_{\mathrm{1}} =\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{8}}−\frac{\sqrt{\mathrm{8}{x}−\mathrm{15}}}{\mathrm{8}} \\ $$$$\mathrm{defined}\:\mathrm{for}\:{x}\in\left[\frac{\mathrm{15}}{\mathrm{8}};\:+\infty\right] \\ $$$${y}_{\mathrm{1}} '=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{8}{x}−\mathrm{15}}}=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{2} \\ $$$${y}_{\mathrm{1}} ''=\frac{\mathrm{2}}{\left(\mathrm{8}{x}−\mathrm{15}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} };\:{x}=\mathrm{2}\:\Rightarrow\:{y}_{\mathrm{2}} ''=\mathrm{2}>\mathrm{0}\:\Rightarrow\:\mathrm{min}\:\mathrm{at}\:\begin{pmatrix}{\mathrm{2}}\\{\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{range}=\left[\mathrm{1};\:+\infty\right] \\ $$$${y}_{\mathrm{2}} =\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{8}}+\frac{\sqrt{\mathrm{8}{x}−\mathrm{15}}}{\mathrm{8}} \\ $$$$\mathrm{defined}\:\mathrm{for}\:{x}\in\left[\frac{\mathrm{15}}{\mathrm{8}};\:+\infty\right] \\ $$$${y}_{\mathrm{2}} '=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{8}{x}−\mathrm{15}}}=\mathrm{0}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{range}=\left[\frac{\mathrm{17}}{\mathrm{16}};\:+\infty\right] \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=\begin{cases}{\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{8}}−\frac{\sqrt{\mathrm{8}{x}−\mathrm{15}}}{\mathrm{8}};\:{x}\in\left[\frac{\mathrm{15}}{\mathrm{8}};\:\mathrm{2}\right]}\\{\left.\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{8}}+\frac{\sqrt{\mathrm{8}{x}−\mathrm{15}}}{\mathrm{8}};\:{x}\in\right]\frac{\mathrm{15}}{\mathrm{8}};\:+\infty\left[\right.}\end{cases} \\ $$$$\int{f}^{−\mathrm{1}} \left({x}\right){dx}=\begin{cases}{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+\frac{{x}}{\mathrm{8}}−\frac{\left(\mathrm{8}{x}−\mathrm{15}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{96}};\:{x}\in\left[\frac{\mathrm{15}}{\mathrm{8}};\:\mathrm{2}\right]}\\{\left.\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+\frac{{x}}{\mathrm{8}}+\frac{\left(\mathrm{8}{x}−\mathrm{15}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{96}};\:{x}\in\right]\frac{\mathrm{15}}{\mathrm{8}};\:+\infty\left[\right.}\end{cases} \\ $$$$\mathrm{but}\:\mathrm{of}\:\mathrm{course}\:\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{the}\:\mathrm{area}\:\mathrm{between} \\ $$$$\mathrm{this}\:\mathrm{function}\:\mathrm{and}\:\mathrm{the}\:{x}−\mathrm{axis}\:\mathrm{you}\:\mathrm{must}\:\mathrm{take} \\ $$$$\int{f}^{−\mathrm{1}} \left({x}\right){dx}=\begin{cases}{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+\frac{{x}}{\mathrm{8}}−\frac{\left(\mathrm{8}{x}−\mathrm{15}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{96}};\:{x}\in\left[\frac{\mathrm{15}}{\mathrm{8}};\:\mathrm{2}\right]}\\{\left.\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+\frac{{x}}{\mathrm{8}}+\frac{\left(\mathrm{8}{x}−\mathrm{15}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{96}};\:{x}\in\right]\mathrm{2};\:+\infty\left[\right.}\end{cases} \\ $$
Commented by math khazana by abdo last updated on 03/Aug/18
$${thank}\:{you}\:{sir}\:{mjs}\:{for}\:{this}\:{hard}\:{work}\:. \\ $$
