Menu Close

Let-f-x-2x-x-2-4-a-Find-b-b-f-x-dx-for-b-gt-0-b-Determine-f-x-dx-is-convergent-or-not-

Tinku Tara 0 Comments
Pin




Question Number 53212 by Joel578 last updated on 19/Jan/19
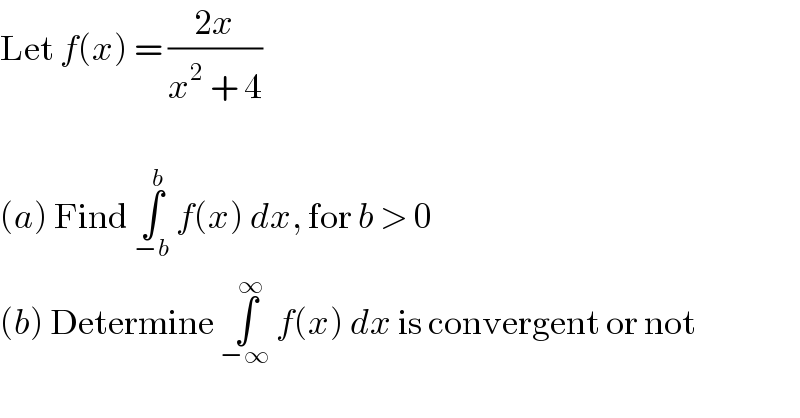
Let f(x) = ((2x)/(x^2 + 4)) (a) Find ∫_(−b) ^b f(x) dx, for b > 0 (b) Determine ∫_(−∞) ^∞ f(x) dx is convergent or not
$$\mathrm{Let}\:{f}\left({x}\right)\:=\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+\:\mathrm{4}} \\ $$$$ \\ $$$$\left({a}\right)\:\mathrm{Find}\:\underset{−{b}} {\overset{{b}} {\int}}\:{f}\left({x}\right)\:{dx},\:\mathrm{for}\:{b}\:>\:\mathrm{0} \\ $$$$\left({b}\right)\:\mathrm{Determine}\:\underset{−\infty} {\overset{\infty} {\int}}\:{f}\left({x}\right)\:{dx}\:\mathrm{is}\:\mathrm{convergent}\:\mathrm{or}\:\mathrm{not} \\ $$
Commented by Joel578 last updated on 19/Jan/19
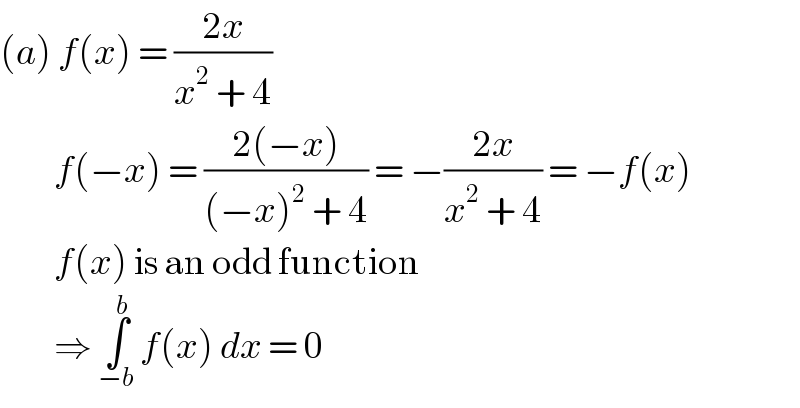
(a) f(x) = ((2x)/(x^2 + 4)) f(−x) = ((2(−x))/((−x)^2 + 4)) = −((2x)/(x^2 + 4)) = −f(x) f(x) is an odd function ⇒ ∫_(−b) ^b f(x) dx = 0
$$\left({a}\right)\:{f}\left({x}\right)\:=\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+\:\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:{f}\left(−{x}\right)\:=\:\frac{\mathrm{2}\left(−{x}\right)}{\left(−{x}\right)^{\mathrm{2}} \:+\:\mathrm{4}}\:=\:−\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+\:\mathrm{4}}\:=\:−{f}\left({x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{function} \\ $$$$\:\:\:\:\:\:\:\:\:\Rightarrow\:\underset{−{b}} {\overset{{b}} {\int}}\:{f}\left({x}\right)\:{dx}\:=\:\mathrm{0} \\ $$
Commented by Joel578 last updated on 19/Jan/19
Please help with part (b)
$$\mathrm{Please}\:\mathrm{help}\:\mathrm{with}\:\mathrm{part}\:\left({b}\right) \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
1.((2x)/(x^2 +4)) is odd function because f(−x)=−f(x) 2.the intregal ∫_(−b) ^b ((2x)/(x^2 +4))dx=∫_(−b) ^0 ((2x)/(x^2 +4))dx+∫_0 ^b ((2x)/(x^2 +4))dx I=I_1 +I_2 though I_1 =I_2 but I_1 represent area bound by curve ((2x)/(4+x^2 )) from x=−b to x=0 but that area is below x axis so negetive area . I_2 represent the area bound by the curve ((2x)/(4+x^2 )) from x=0 to x=b above x axis so +ve area hence I_1 +I_2 =0 this is my opinion let others comment...
$$\mathrm{1}.\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}\:{is}\:{odd}\:{function}\:\:{because}\:{f}\left(−{x}\right)=−{f}\left({x}\right) \\ $$$$\mathrm{2}.{the}\:{intregal}\:\int_{−{b}} ^{{b}} \frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}=\int_{−{b}} ^{\mathrm{0}} \frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}+\int_{\mathrm{0}} ^{{b}} \frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx} \\ $$$${I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$$${though}\:{I}_{\mathrm{1}} ={I}_{\mathrm{2}} \:{but}\:{I}_{\mathrm{1}} {represent}\:{area}\:{bound}\:{by} \\ $$$${curve}\:\frac{\mathrm{2}{x}}{\mathrm{4}+{x}^{\mathrm{2}} }\:\:{from}\:\:{x}=−{b}\:\:{to}\:{x}=\mathrm{0}\:\:{but}\:{that}\:{area} \\ $$$${is}\:{below}\:{x}\:{axis}\:{so}\:\:{negetive}\:{area}\:. \\ $$$${I}_{\mathrm{2}} \:{represent}\:{the}\:{area}\:{bound}\:{by}\:{the}\:{curve}\:\frac{\mathrm{2}{x}}{\mathrm{4}+{x}^{\mathrm{2}} } \\ $$$${from}\:{x}=\mathrm{0}\:\:{to}\:{x}={b}\:\:{above}\:{x}\:{axis}\:{so}\:+{ve}\:{area} \\ $$$${hence}\:{I}_{\mathrm{1}} +{I}_{\mathrm{2}} =\mathrm{0} \\ $$$${this}\:{is}\:{my}\:{opinion}\:{let}\:{others}\:{comment}… \\ $$$$ \\ $$$$ \\ $$
Commented by afachri last updated on 19/Jan/19
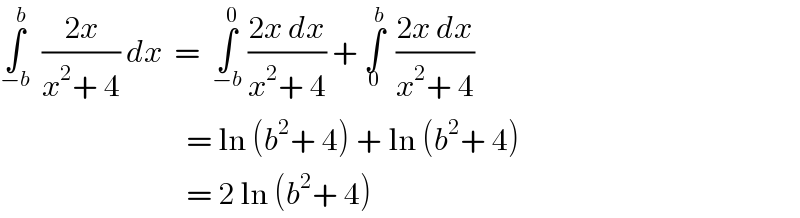
∫_(−b) ^b ((2x)/(x^2 + 4)) dx = ∫_(−b) ^0 ((2x dx)/(x^2 + 4)) + ∫_0 ^b ((2x dx)/(x^2 + 4)) = ln (b^2 + 4) + ln (b^2 + 4) = 2 ln (b^2 + 4)
$$\underset{−{b}} {\overset{{b}} {\int}}\:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\:\mathrm{4}}\:{dx}\:\:=\:\:\underset{−{b}} {\overset{\mathrm{0}} {\int}}\:\frac{\mathrm{2}{x}\:{dx}}{{x}^{\mathrm{2}} +\:\mathrm{4}}\:+\:\underset{\mathrm{0}} {\overset{{b}} {\int}}\:\:\frac{\mathrm{2}{x}\:{dx}}{{x}^{\mathrm{2}} +\:\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{ln}\:\left({b}^{\mathrm{2}} +\:\mathrm{4}\right)\:+\:\mathrm{ln}\:\left({b}^{\mathrm{2}} +\:\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\:\mathrm{ln}\:\left({b}^{\mathrm{2}} +\:\mathrm{4}\right) \\ $$
Commented by afachri last updated on 19/Jan/19
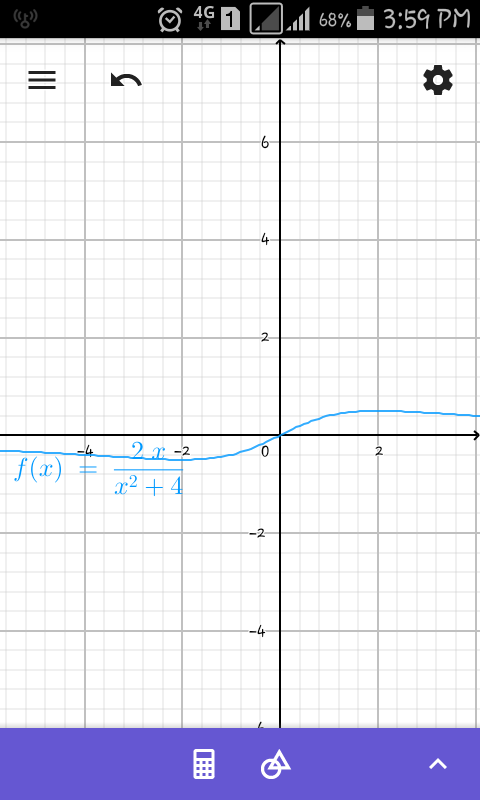
Commented by afachri last updated on 19/Jan/19
in my opinion to the part B, we can define ∫_(−∞) ^∞ f(x) is convergent or not by check the limit. it′s divergent while lim_(x→∞) f(x) = ∞. lim_(x→∞) ((2x)/(x^2 + 4)) = lim_(x→∞) ((x^2 ((2/x)))/(x^2 (1 + (4/x^2 )))) = lim_(x→∞) (0/(1 + 0)) = 0 f(x) = ((2x)/(x^2 + 4)) converges so ∫_(−∞) ^∞ f(x) does.
$$\mathrm{in}\:\mathrm{my}\:\mathrm{opinion}\:\mathrm{to}\:\mathrm{the}\:\mathrm{part}\:\mathrm{B},\:\mathrm{we}\:\mathrm{can}\:\mathrm{define} \\ $$$$\underset{−\infty} {\overset{\infty} {\int}}{f}\left({x}\right)\:\mathrm{is}\:\mathrm{convergent}\:\mathrm{or}\:\mathrm{not}\:\mathrm{by}\:\mathrm{check}\:\mathrm{the} \\ $$$$\mathrm{limit}.\:\mathrm{it}'\mathrm{s}\:\mathrm{divergent}\:\mathrm{while}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{f}\left({x}\right)\:=\:\infty. \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\:\mathrm{4}}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\frac{{x}^{\mathrm{2}} \left(\frac{\mathrm{2}}{{x}}\right)}{{x}^{\mathrm{2}} \left(\mathrm{1}\:+\:\frac{\mathrm{4}}{{x}^{\mathrm{2}} }\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\frac{\mathrm{0}}{\mathrm{1}\:+\:\mathrm{0}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{0} \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\:\mathrm{4}}\:\:\:\mathrm{converges}\:\mathrm{so}\:\underset{−\infty} {\overset{\infty} {\int}}{f}\left({x}\right)\:\mathrm{does}. \\ $$
Commented by afachri last updated on 19/Jan/19
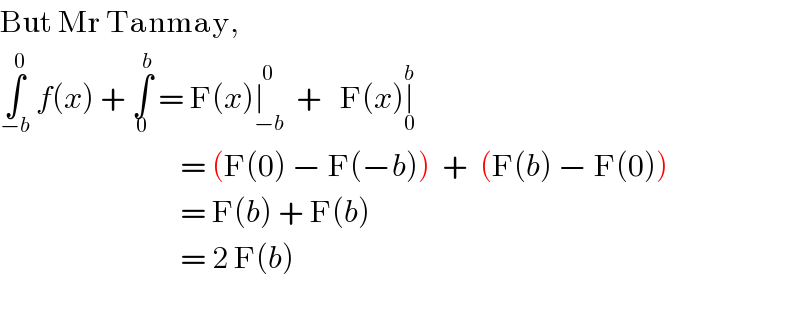
But Mr Tanmay, ∫_(−b) ^0 f(x) + ∫_0 ^b = F(x)∣_(−b) ^0 + F(x)∣_0 ^b = (F(0) − F(−b)) + (F(b) − F(0)) = F(b) + F(b) = 2 F(b)
$$\mathrm{But}\:\mathrm{Mr}\:\mathrm{Tanmay},\: \\ $$$$\underset{−{b}} {\overset{\mathrm{0}} {\int}}\:{f}\left({x}\right)\:+\:\underset{\mathrm{0}} {\overset{{b}} {\int}}\:=\:\mathrm{F}\left({x}\right)\underset{−{b}} {\overset{\mathrm{0}} {\mid}}\:\:+\:\:\:\mathrm{F}\left({x}\right)\underset{\mathrm{0}} {\overset{{b}} {\mid}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{F}\left(\mathrm{0}\right)\:−\:\mathrm{F}\left(−{b}\right)\right)\:\:+\:\:\left(\mathrm{F}\left({b}\right)\:−\:\mathrm{F}\left(\mathrm{0}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{F}\left({b}\right)\:+\:\mathrm{F}\left({b}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\:\mathrm{F}\left({b}\right) \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
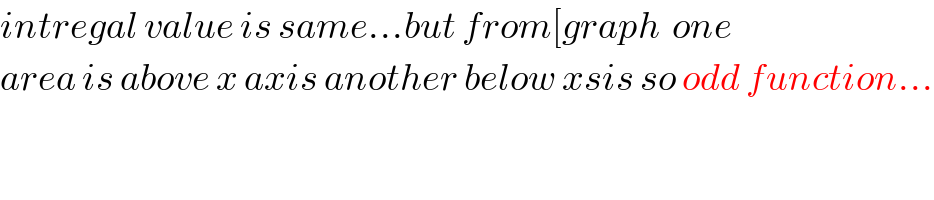
intregal value is same...but from[graph one area is above x axis another below xsis so odd function...
$${intregal}\:{value}\:{is}\:{same}…{but}\:{from}\left[{graph}\:\:{one}\right. \\ $$$${area}\:{is}\:{above}\:{x}\:{axis}\:{another}\:{below}\:{xsis}\:{so}\:{odd}\:{function}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
Commented by afachri last updated on 19/Jan/19
thank you Mr Damian and all of you Sir who have corrected me for my mistake. what an interesting forum here. now i′m understand it.
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Mr}\:\mathrm{Damian}\:\mathrm{and}\:\mathrm{all}\:\mathrm{of}\:\mathrm{you}\:\mathrm{Sir} \\ $$$$\mathrm{who}\:\mathrm{have}\:\mathrm{corrected}\:\mathrm{me}\:\mathrm{for}\:\mathrm{my}\:\mathrm{mistake}.\: \\ $$$$\mathrm{what}\:\mathrm{an}\:\mathrm{interesting}\:\mathrm{forum}\:\mathrm{here}.\:\mathrm{now}\:\mathrm{i}'\mathrm{m} \\ $$$$\mathrm{understand}\:\mathrm{it}. \\ $$
Commented by afachri last updated on 19/Jan/19
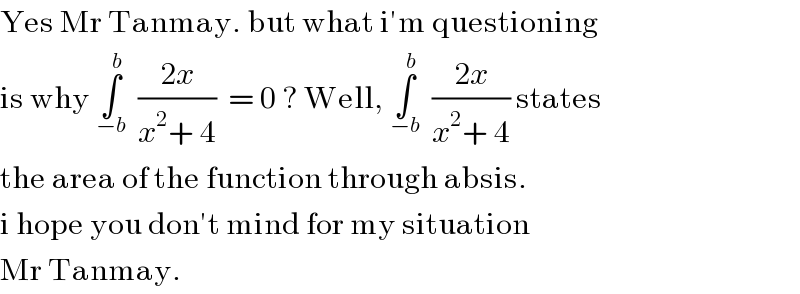
Yes Mr Tanmay. but what i′m questioning is why ∫_(−b) ^b ((2x)/(x^2 + 4)) = 0 ? Well, ∫_(−b) ^b ((2x)/(x^2 + 4)) states the area of the function through absis. i hope you don′t mind for my situation Mr Tanmay.
$$\mathrm{Yes}\:\mathrm{Mr}\:\mathrm{Tanmay}.\:\mathrm{but}\:\mathrm{what}\:\mathrm{i}'\mathrm{m}\:\mathrm{questioning} \\ $$$$\mathrm{is}\:\mathrm{why}\:\underset{−{b}} {\overset{{b}} {\int}}\:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\:\mathrm{4}}\:\:=\:\mathrm{0}\:?\:\mathrm{Well},\:\underset{−{b}} {\overset{{b}} {\int}}\:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\:\mathrm{4}}\:\mathrm{states} \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:\mathrm{through}\:\mathrm{absis}.\: \\ $$$$\mathrm{i}\:\mathrm{hope}\:\mathrm{you}\:\mathrm{don}'\mathrm{t}\:\mathrm{mind}\:\mathrm{for}\:\mathrm{my}\:\mathrm{situation}\: \\ $$$$\mathrm{Mr}\:\mathrm{Tanmay}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
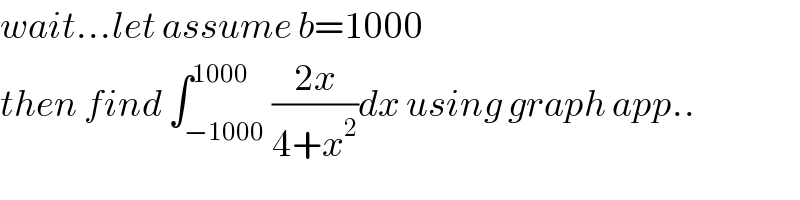
wait...let assume b=1000 then find ∫_(−1000) ^(1000) ((2x)/(4+x^2 ))dx using graph app..
$${wait}…{let}\:{assume}\:{b}=\mathrm{1000} \\ $$$${then}\:{find}\:\int_{−\mathrm{1000}} ^{\mathrm{1000}} \frac{\mathrm{2}{x}}{\mathrm{4}+{x}^{\mathrm{2}} }{dx}\:{using}\:{graph}\:{app}.. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
Commented by afachri last updated on 19/Jan/19
Yes Mr Tanmay. Done. Thank You so much. Really appreciate your time Mr Tanmay
$$\mathrm{Yes}\:\mathrm{Mr}\:\mathrm{Tanmay}.\:\mathrm{Done}.\:\mathrm{Thank}\:\mathrm{You} \\ $$$$\mathrm{so}\:\mathrm{much}.\:\mathrm{Really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$$$\mathrm{Mr}\:\mathrm{Tanmay} \\ $$
Commented by afachri last updated on 19/Jan/19
Commented by JDamian last updated on 19/Jan/19
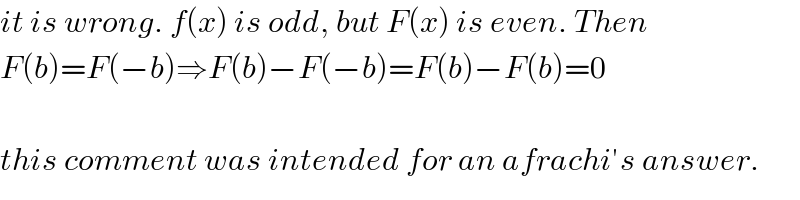
it is wrong. f(x) is odd, but F(x) is even. Then F(b)=F(−b)⇒F(b)−F(−b)=F(b)−F(b)=0 this comment was intended for an afrachi′s answer.
$${it}\:{is}\:{wrong}.\:{f}\left({x}\right)\:{is}\:{odd},\:{but}\:{F}\left({x}\right)\:{is}\:{even}.\:{Then} \\ $$$${F}\left({b}\right)={F}\left(−{b}\right)\Rightarrow{F}\left({b}\right)−{F}\left(−{b}\right)={F}\left({b}\right)−{F}\left({b}\right)=\mathrm{0} \\ $$$$ \\ $$$${this}\:{comment}\:{was}\:{intended}\:{for}\:{an}\:{afrachi}'{s}\:{answer}. \\ $$
Commented by Joel578 last updated on 20/Jan/19
Thanks you Sir afachri, tanmay, JDamian for the answers. Actually I′m agree with Sir tanmay. That′s what I have been taught in Calculus 1. There is a difference between a definite integral and a definite integral as an area
$$\mathrm{Thanks}\:\mathrm{you}\:\mathrm{Sir}\:\mathrm{afachri},\:\mathrm{tanmay},\:\mathrm{JDamian}\:\mathrm{for}\:\mathrm{the}\:\mathrm{answers}. \\ $$$$\mathrm{Actually}\:\mathrm{I}'\mathrm{m}\:\mathrm{agree}\:\mathrm{with}\:\mathrm{Sir}\:\mathrm{tanmay}.\:\mathrm{That}'\mathrm{s}\: \\ $$$$\mathrm{what}\:\mathrm{I}\:\mathrm{have}\:\mathrm{been}\:\mathrm{taught}\:\mathrm{in}\:\mathrm{Calculus}\:\mathrm{1}. \\ $$$$\mathrm{There}\:\mathrm{is}\:\mathrm{a}\:\mathrm{difference}\:\mathrm{between}\:\mathrm{a}\:\mathrm{definite}\:\mathrm{integral} \\ $$$$\mathrm{and}\:\mathrm{a}\:\mathrm{definite}\:\mathrm{integral}\:\mathrm{as}\:\mathrm{an}\:\mathrm{area} \\ $$
Commented by maxmathsup by imad last updated on 23/Jan/19
for all odd function integrable on ]−a,a[ a∈R^− we have ∫_(−a) ^a f(x)dx =0.
$$\left.{for}\:{all}\:\:{odd}\:{function}\:\:{integrable}\:{on}\:\right]−{a},{a}\left[\:{a}\in\overset{−} {{R}}\:\:\:{we}\:{have}\:\right. \\ $$$$\int_{−{a}} ^{{a}} {f}\left({x}\right){dx}\:=\mathrm{0}. \\ $$
Answered by MJS last updated on 20/Jan/19
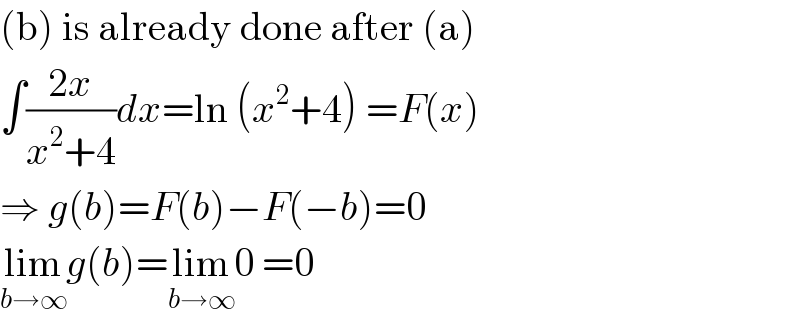
(b) is already done after (a) ∫((2x)/(x^2 +4))dx=ln (x^2 +4) =F(x) ⇒ g(b)=F(b)−F(−b)=0 lim_(b→∞) g(b)=lim_(b→∞) 0 =0
$$\left(\mathrm{b}\right)\:\mathrm{is}\:\mathrm{already}\:\mathrm{done}\:\mathrm{after}\:\left(\mathrm{a}\right) \\ $$$$\int\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}=\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{4}\right)\:={F}\left({x}\right) \\ $$$$\Rightarrow\:{g}\left({b}\right)={F}\left({b}\right)−{F}\left(−{b}\right)=\mathrm{0} \\ $$$$\underset{{b}\rightarrow\infty} {\mathrm{lim}}{g}\left({b}\right)=\underset{{b}\rightarrow\infty} {\mathrm{lim}0}\:=\mathrm{0} \\ $$
Commented by Joel578 last updated on 20/Jan/19
thank you very much
$${thank}\:{you}\:{very}\:{much} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
b) it is my opinion... ∫_(−∞) ^(+∞) f(x)dx lim_(h→−∞) ∫_h ^0 f(x) dx=−ve A lim_(k→+∞) ∫_0 ^k f(x)dx=+ve A so ∫_(−∞) ^(+∞) ((2x)/(4+x^2 ))dx=0 anoother way... x=2tanθ dx=2sec^2 θdθ ∫_(−(π/2)) ^(π/2) ((2×2tanθ×2sec^2 θdθ)/(4+4tan^2 θ)) =∫_(−(π/2)) ^(π/2) ((8tanθsec^2 θ)/(4sec^2 θ))dθ =2∣lnsecθ∣_(−(π/2)) ^(π/2) =−2∣lncosθ∣_(−(π/2)) ^(π/2) =−2[lncos((π/2))−lncos(−(π/2))] =0 it is my opinion...let others comment...
$$\left.{b}\right)\:{it}\:{is}\:{my}\:{opinion}… \\ $$$$\int_{−\infty} ^{+\infty} {f}\left({x}\right){dx} \\ $$$$\underset{{h}\rightarrow−\infty} {\mathrm{lim}}\int_{{h}} ^{\mathrm{0}} \:{f}\left({x}\right)\:{dx}=−{ve}\:{A} \\ $$$$\underset{{k}\rightarrow+\infty} {\mathrm{lim}}\:\int_{\mathrm{0}} ^{{k}} {f}\left({x}\right){dx}=+{ve}\:{A} \\ $$$${so}\:\int_{−\infty} ^{+\infty} \frac{\mathrm{2}{x}}{\mathrm{4}+{x}^{\mathrm{2}} }{dx}=\mathrm{0} \\ $$$${anoother}\:{way}… \\ $$$${x}=\mathrm{2}{tan}\theta\:\:{dx}=\mathrm{2}{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}×\mathrm{2}{tan}\theta×\mathrm{2}{sec}^{\mathrm{2}} \theta{d}\theta}{\mathrm{4}+\mathrm{4}{tan}^{\mathrm{2}} \theta} \\ $$$$=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{8}{tan}\theta{sec}^{\mathrm{2}} \theta}{\mathrm{4}{sec}^{\mathrm{2}} \theta}{d}\theta \\ $$$$=\mathrm{2}\mid{lnsec}\theta\mid_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=−\mathrm{2}\mid{lncos}\theta\mid_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=−\mathrm{2}\left[{lncos}\left(\frac{\pi}{\mathrm{2}}\right)−{lncos}\left(−\frac{\pi}{\mathrm{2}}\right)\right] \\ $$$$=\mathrm{0} \\ $$$${it}\:{is}\:{my}\:{opinion}…{let}\:{others}\:{comment}… \\ $$
Commented by Joel578 last updated on 20/Jan/19
thank you very much
$${thank}\:{you}\:{very}\:{much} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *