Menu Close

let-f-x-3-2-cosx-developp-f-ar-fourier-serie-

Tinku Tara 0 Comments
Pin




Question Number 34913 by abdo imad last updated on 12/May/18
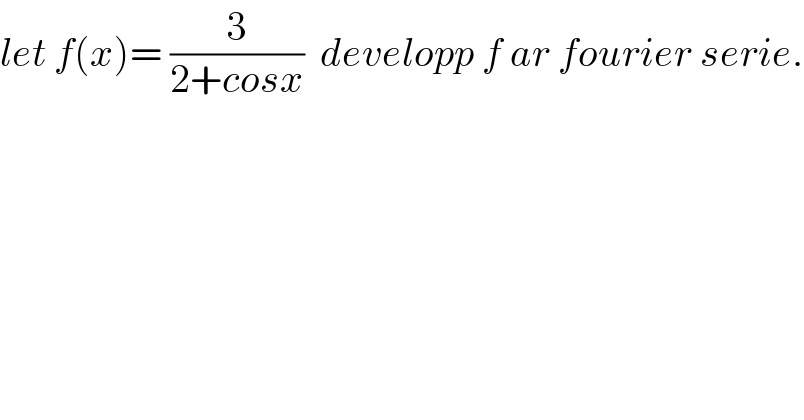
let f(x)= (3/(2+cosx)) developp f ar fourier serie.
$${let}\:{f}\left({x}\right)=\:\frac{\mathrm{3}}{\mathrm{2}+{cosx}}\:\:{developp}\:{f}\:{ar}\:{fourier}\:{serie}. \\ $$
Commented by abdo imad last updated on 31/May/18
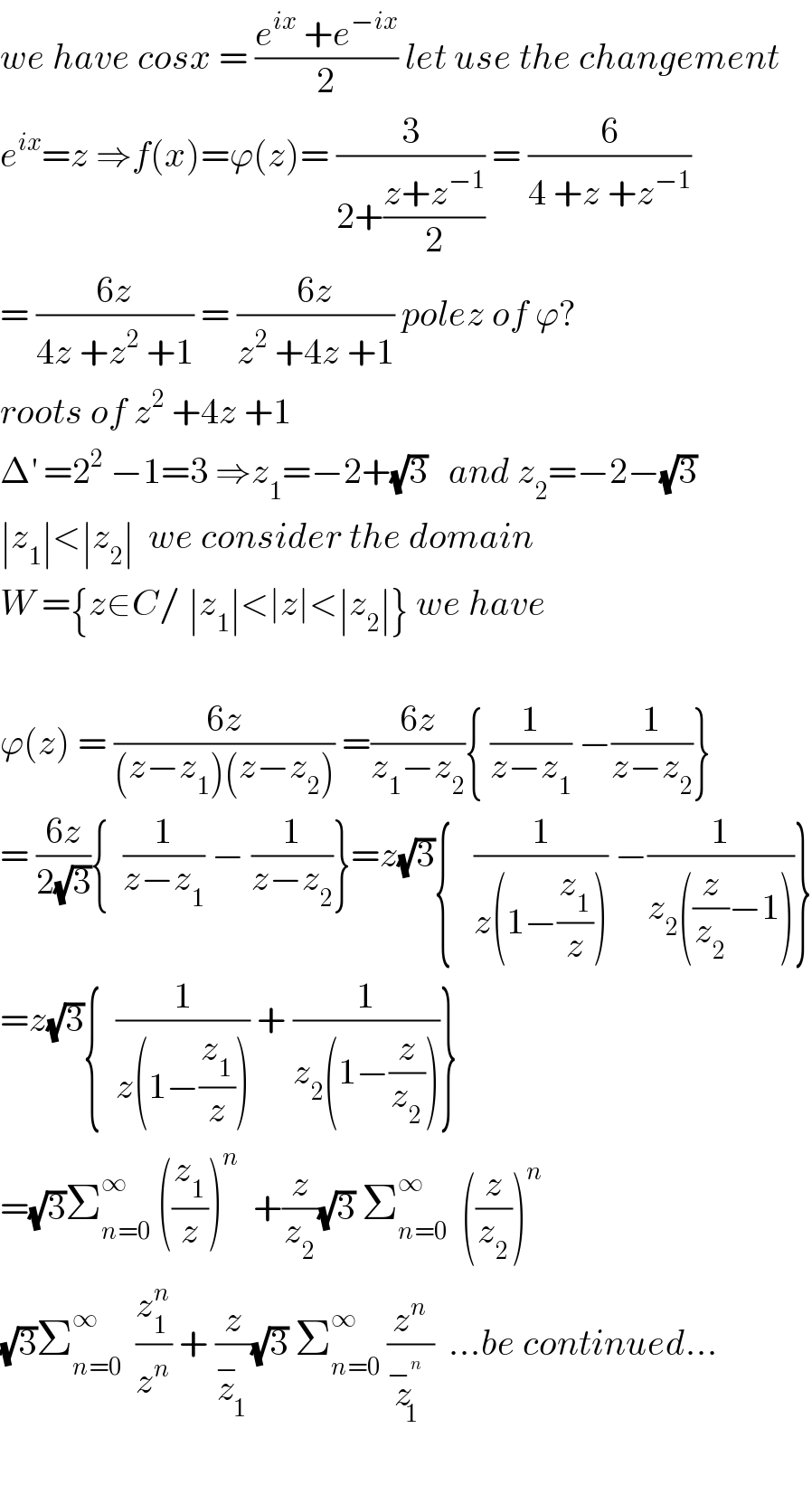
we have cosx = ((e^(ix) +e^(−ix) )/2) let use the changement e^(ix) =z ⇒f(x)=ϕ(z)= (3/(2+((z+z^(−1) )/2))) = (6/(4 +z +z^(−1) )) = ((6z)/(4z +z^2 +1)) = ((6z)/(z^2 +4z +1)) polez of ϕ? roots of z^2 +4z +1 Δ^′ =2^2 −1=3 ⇒z_1 =−2+(√3) and z_2 =−2−(√3) ∣z_1 ∣<∣z_2 ∣ we consider the domain W ={z∈C/ ∣z_1 ∣<∣z∣<∣z_2 ∣} we have ϕ(z) = ((6z)/((z−z_1 )(z−z_2 ))) =((6z)/(z_1 −z_2 )){ (1/(z−z_1 )) −(1/(z−z_2 ))} = ((6z)/(2(√3))){ (1/(z−z_1 )) − (1/(z−z_2 ))}=z(√3){ (1/(z(1−(z_1 /z)))) −(1/(z_2 ((z/z_2 )−1)))} =z(√3){ (1/(z(1−(z_1 /z)))) + (1/(z_2 (1−(z/z_2 ))))} =(√3)Σ_(n=0) ^∞ ((z_1 /z))^n +(z/z_2 )(√3) Σ_(n=0) ^∞ ((z/z_2 ))^n (√3)Σ_(n=0) ^∞ (z_1 ^n /z^n ) + (z/z_1 ^− )(√3) Σ_(n=0) ^∞ (z^n /z_1 ^−^n ) ...be continued...
$${we}\:{have}\:{cosx}\:=\:\frac{{e}^{{ix}} \:+{e}^{−{ix}} }{\mathrm{2}}\:{let}\:{use}\:{the}\:{changement} \\ $$$${e}^{{ix}} ={z}\:\Rightarrow{f}\left({x}\right)=\varphi\left({z}\right)=\:\frac{\mathrm{3}}{\mathrm{2}+\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}}\:=\:\frac{\mathrm{6}}{\mathrm{4}\:+{z}\:+{z}^{−\mathrm{1}} } \\ $$$$=\:\frac{\mathrm{6}{z}}{\mathrm{4}{z}\:+{z}^{\mathrm{2}} \:+\mathrm{1}}\:=\:\frac{\mathrm{6}{z}}{{z}^{\mathrm{2}} \:+\mathrm{4}{z}\:+\mathrm{1}}\:{polez}\:{of}\:\varphi? \\ $$$${roots}\:{of}\:{z}^{\mathrm{2}} \:+\mathrm{4}{z}\:+\mathrm{1} \\ $$$$\Delta^{'} \:=\mathrm{2}^{\mathrm{2}} \:−\mathrm{1}=\mathrm{3}\:\Rightarrow{z}_{\mathrm{1}} =−\mathrm{2}+\sqrt{\mathrm{3}}\:\:\:{and}\:{z}_{\mathrm{2}} =−\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\mid{z}_{\mathrm{1}} \mid<\mid{z}_{\mathrm{2}} \mid\:\:{we}\:{consider}\:{the}\:{domain} \\ $$$${W}\:=\left\{{z}\in{C}/\:\mid{z}_{\mathrm{1}} \mid<\mid{z}\mid<\mid{z}_{\mathrm{2}} \mid\right\}\:{we}\:{have} \\ $$$$ \\ $$$$\varphi\left({z}\right)\:=\:\frac{\mathrm{6}{z}}{\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)}\:=\frac{\mathrm{6}{z}}{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} }\left\{\:\frac{\mathrm{1}}{{z}−{z}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{z}−{z}_{\mathrm{2}} }\right\} \\ $$$$=\:\frac{\mathrm{6}{z}}{\mathrm{2}\sqrt{\mathrm{3}}}\left\{\:\:\frac{\mathrm{1}}{{z}−{z}_{\mathrm{1}} }\:−\:\frac{\mathrm{1}}{{z}−{z}_{\mathrm{2}} }\right\}={z}\sqrt{\mathrm{3}}\left\{\:\:\:\frac{\mathrm{1}}{{z}\left(\mathrm{1}−\frac{{z}_{\mathrm{1}} }{{z}}\right)}\:−\frac{\mathrm{1}}{{z}_{\mathrm{2}} \left(\frac{{z}}{{z}_{\mathrm{2}} }−\mathrm{1}\right)}\right\} \\ $$$$={z}\sqrt{\mathrm{3}}\left\{\:\:\frac{\mathrm{1}}{{z}\left(\mathrm{1}−\frac{{z}_{\mathrm{1}} }{{z}}\right)}\:+\:\frac{\mathrm{1}}{{z}_{\mathrm{2}} \left(\mathrm{1}−\frac{{z}}{{z}_{\mathrm{2}} }\right)}\right\} \\ $$$$=\sqrt{\mathrm{3}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{{z}_{\mathrm{1}} }{{z}}\right)^{{n}} \:\:+\frac{{z}}{{z}_{\mathrm{2}} }\sqrt{\mathrm{3}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(\frac{{z}}{{z}_{\mathrm{2}} }\right)^{{n}} \\ $$$$\sqrt{\mathrm{3}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{z}_{\mathrm{1}} ^{{n}} }{{z}^{{n}} }\:+\:\frac{{z}}{\overset{−} {{z}}_{\mathrm{1}} }\sqrt{\mathrm{3}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{z}^{{n}} }{\overset{−^{{n}} } {{z}}_{\mathrm{1}} }\:\:…{be}\:{continued}… \\ $$$$ \\ $$
Commented by abdo imad last updated on 31/May/18
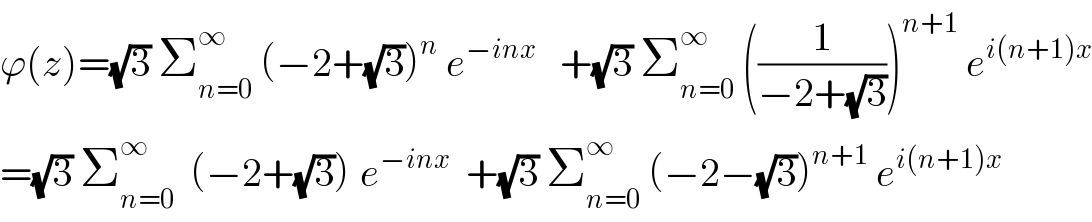
ϕ(z)=(√3) Σ_(n=0) ^∞ (−2+(√3))^n e^(−inx) +(√3) Σ_(n=0) ^∞ ((1/(−2+(√3))))^(n+1) e^(i(n+1)x) =(√3) Σ_(n=0) ^∞ (−2+(√3))^ e^(−inx) +(√3) Σ_(n=0) ^∞ (−2−(√3))^(n+1) e^(i(n+1)x)
$$\varphi\left({z}\right)=\sqrt{\mathrm{3}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{n}} \:{e}^{−{inx}} \:\:\:+\sqrt{\mathrm{3}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{1}}{−\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{n}+\mathrm{1}} \:{e}^{{i}\left({n}+\mathrm{1}\right){x}} \\ $$$$=\sqrt{\mathrm{3}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{2}+\sqrt{\mathrm{3}}\right)^{} {e}^{−{inx}} \:\:+\sqrt{\mathrm{3}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{2}−\sqrt{\mathrm{3}}\right)^{{n}+\mathrm{1}} \:{e}^{{i}\left({n}+\mathrm{1}\right){x}} \\ $$
Commented by abdo.msup.com last updated on 31/May/18
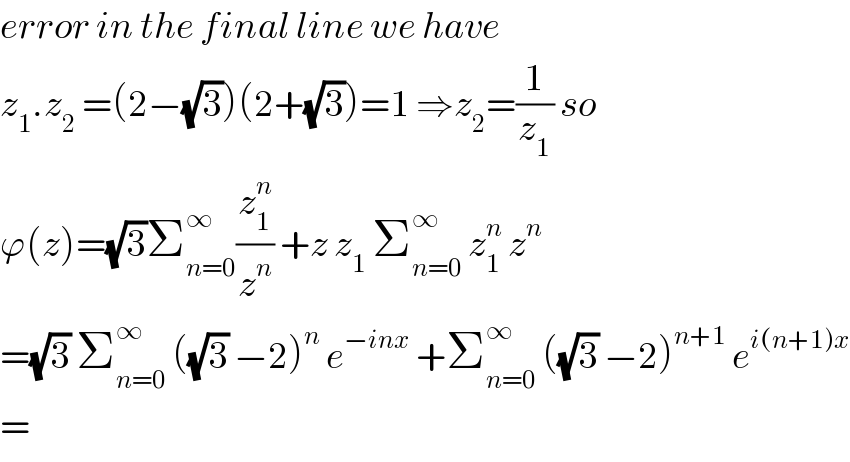
error in the final line we have z_1 .z_2 =(2−(√3))(2+(√3))=1 ⇒z_2 =(1/z_1 ) so ϕ(z)=(√3)Σ_(n=0) ^∞ (z_1 ^n /z^n ) +z z_1 Σ_(n=0) ^∞ z_1 ^n z^n =(√3) Σ_(n=0) ^∞ ((√3) −2)^n e^(−inx) +Σ_(n=0) ^∞ ((√3) −2)^(n+1) e^(i(n+1)x) =
$${error}\:{in}\:{the}\:{final}\:{line}\:{we}\:{have} \\ $$$${z}_{\mathrm{1}} .{z}_{\mathrm{2}} \:=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)=\mathrm{1}\:\Rightarrow{z}_{\mathrm{2}} =\frac{\mathrm{1}}{{z}_{\mathrm{1}} }\:{so} \\ $$$$\varphi\left({z}\right)=\sqrt{\mathrm{3}}\sum_{{n}=\mathrm{0}} ^{\infty} \frac{{z}_{\mathrm{1}} ^{{n}} }{{z}^{{n}} }\:+{z}\:{z}_{\mathrm{1}} \:\sum_{{n}=\mathrm{0}} ^{\infty} \:{z}_{\mathrm{1}} ^{{n}} \:{z}^{{n}} \\ $$$$=\sqrt{\mathrm{3}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\sqrt{\mathrm{3}}\:−\mathrm{2}\right)^{{n}} \:{e}^{−{inx}} \:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\sqrt{\mathrm{3}}\:−\mathrm{2}\right)^{{n}+\mathrm{1}} \:{e}^{{i}\left({n}+\mathrm{1}\right){x}} \\ $$$$= \\ $$
Commented by prof Abdo imad last updated on 01/Jun/18
method of Residus f is 2π periodic even so f(x) = (a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx) with a_n = (2/T) ∫_([T]) f(x) cos(nx)dx = (2/(2π)) ∫_0 ^(2π) ((3 cos(nx))/(2+cosx)) dx = (3/π) ∫_0 ^(2π) ((cos(nx))/(2 +cosx))dx ⇒ (π/3)a_n = ∫_0 ^(2π) ((cos(nx))/(2+cosx))dx changement e^(ix) =z give (π/3)a_n =Re( ∫_0 ^(2π) (e^(inx) /(2 +cosx))dx) =Re( A_n ) but A_n = ∫_(∣z∣=1) (z^n /(2 + ((z +z^(−1) )/2))) (dz/(iz)) = ∫_(∣z∣=1) ((2z^n )/(iz( 4 +z+z^(−1) )))dz = ∫_(∣z∣=1) ((−2iz^n )/(4z +z^2 +1))dz = ∫_(∣z∣=1) ((−2i z^n )/(z^2 +4z +1))dz let introduce the complex function ϕ(z) = ((−2i z^n )/(z^2 +4z?+1)) poles of ϕ? roots of z^2 +4z +1 Δ^′ = 2^2 −1=3 ⇒ z_1 = −2+(√3) and z_2 =−2−(√3) ∣z_1 ∣ −1=2−(√3) −1=1−(√3) <0 ⇒ ∣z_1 ∣<1 ∣z_2 ∣ −1 =2+(√3) −1 = 1+(√3)>0 ⇒ ∣z_2 ∣>1 to eliminate from residus
$${method}\:{of}\:{Residus}\:{f}\:{is}\:\mathrm{2}\pi\:{periodic}\:{even}\:{so} \\ $$$${f}\left({x}\right)\:=\:\frac{{a}_{\mathrm{0}} }{\mathrm{2}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:{a}_{{n}} \:{cos}\left({nx}\right)\:{with} \\ $$$${a}_{{n}} \:=\:\frac{\mathrm{2}}{{T}}\:\int_{\left[{T}\right]} \:\:{f}\left({x}\right)\:{cos}\left({nx}\right){dx} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{2}\pi}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{\mathrm{3}\:{cos}\left({nx}\right)}{\mathrm{2}+{cosx}}\:{dx}\:=\:\frac{\mathrm{3}}{\pi}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{cos}\left({nx}\right)}{\mathrm{2}\:+{cosx}}{dx}\:\Rightarrow \\ $$$$\frac{\pi}{\mathrm{3}}{a}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{cos}\left({nx}\right)}{\mathrm{2}+{cosx}}{dx}\:\:{changement}\:\:{e}^{{ix}} \:={z}\:{give} \\ $$$$\frac{\pi}{\mathrm{3}}{a}_{{n}} \:={Re}\left(\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{e}^{{inx}} }{\mathrm{2}\:+{cosx}}{dx}\right)\:={Re}\left(\:{A}_{{n}} \right)\:{but} \\ $$$${A}_{{n}} \:\:=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{{z}^{{n}} }{\mathrm{2}\:+\:\frac{{z}\:+{z}^{−\mathrm{1}} }{\mathrm{2}}}\:\frac{{dz}}{{iz}} \\ $$$$=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{2}{z}^{{n}} }{{iz}\left(\:\mathrm{4}\:+{z}+{z}^{−\mathrm{1}} \right)}{dz} \\ $$$$=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{−\mathrm{2}{iz}^{{n}} }{\mathrm{4}{z}\:+{z}^{\mathrm{2}} \:+\mathrm{1}}{dz}\: \\ $$$$=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{−\mathrm{2}{i}\:{z}^{{n}} }{{z}^{\mathrm{2}} \:+\mathrm{4}{z}\:+\mathrm{1}}{dz}\:{let}\:{introduce}\:{the}\:{complex} \\ $$$${function}\:\varphi\left({z}\right)\:=\:\frac{−\mathrm{2}{i}\:{z}^{{n}} }{{z}^{\mathrm{2}} \:+\mathrm{4}{z}?+\mathrm{1}}\:{poles}\:{of}\:\varphi? \\ $$$${roots}\:{of}\:{z}^{\mathrm{2}} \:+\mathrm{4}{z}\:+\mathrm{1} \\ $$$$\Delta^{'} =\:\mathrm{2}^{\mathrm{2}} −\mathrm{1}=\mathrm{3}\:\Rightarrow\:{z}_{\mathrm{1}} =\:−\mathrm{2}+\sqrt{\mathrm{3}}\:\:\:{and}\:{z}_{\mathrm{2}} =−\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\mid{z}_{\mathrm{1}} \mid\:−\mathrm{1}=\mathrm{2}−\sqrt{\mathrm{3}}\:−\mathrm{1}=\mathrm{1}−\sqrt{\mathrm{3}}\:<\mathrm{0}\:\Rightarrow\:\mid{z}_{\mathrm{1}} \mid<\mathrm{1} \\ $$$$\mid{z}_{\mathrm{2}} \mid\:−\mathrm{1}\:=\mathrm{2}+\sqrt{\mathrm{3}}\:−\mathrm{1}\:=\:\mathrm{1}+\sqrt{\mathrm{3}}>\mathrm{0}\:\Rightarrow\:\mid{z}_{\mathrm{2}} \mid>\mathrm{1}\:{to} \\ $$$${eliminate}\:{from}\:{residus} \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 01/Jun/18
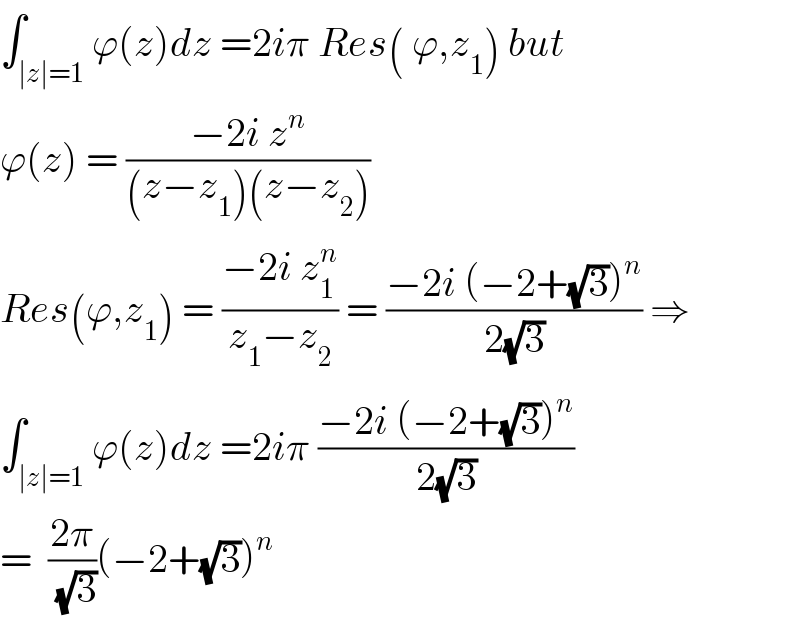
∫_(∣z∣=1) ϕ(z)dz =2iπ Res( ϕ,z_1 ) but ϕ(z) = ((−2i z^n )/((z−z_1 )(z−z_2 ))) Res(ϕ,z_1 ) = ((−2i z_1 ^n )/(z_1 −z_2 )) = ((−2i (−2+(√3))^n )/(2(√3))) ⇒ ∫_(∣z∣=1) ϕ(z)dz =2iπ ((−2i (−2+(√3))^n )/(2(√3))) = ((2π)/( (√3)))(−2+(√3))^n
$$\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\:\varphi,{z}_{\mathrm{1}} \right)\:{but} \\ $$$$\varphi\left({z}\right)\:=\:\frac{−\mathrm{2}{i}\:{z}^{{n}} }{\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)} \\ $$$${Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:=\:\frac{−\mathrm{2}{i}\:{z}_{\mathrm{1}} ^{{n}} }{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} }\:=\:\frac{−\mathrm{2}{i}\:\left(−\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{n}} }{\mathrm{2}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\frac{−\mathrm{2}{i}\:\left(−\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{n}} }{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$=\:\:\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\left(−\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{n}} \\ $$
Commented by abdo.msup.com last updated on 01/Jun/18
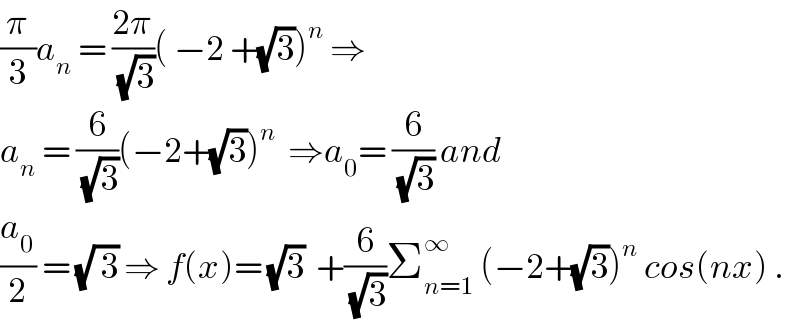
(π/3)a_n = ((2π)/( (√3)))( −2 +(√3))^n ⇒ a_n = (6/( (√3)))(−2+(√3))^n ⇒a_0 = (6/( (√3))) and (a_0 /2) = (√( 3)) ⇒ f(x)= (√3) +(6/( (√3)))Σ_(n=1) ^∞ (−2+(√3))^n cos(nx) .
$$\frac{\pi}{\mathrm{3}}{a}_{{n}} \:=\:\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\left(\:−\mathrm{2}\:+\sqrt{\mathrm{3}}\right)^{{n}} \:\Rightarrow \\ $$$${a}_{{n}} \:=\:\frac{\mathrm{6}}{\:\sqrt{\mathrm{3}}}\left(−\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{n}} \:\:\Rightarrow{a}_{\mathrm{0}} =\:\frac{\mathrm{6}}{\:\sqrt{\mathrm{3}}}\:{and} \\ $$$$\frac{{a}_{\mathrm{0}} }{\mathrm{2}}\:=\:\sqrt{\:\mathrm{3}}\:\Rightarrow\:{f}\left({x}\right)=\:\sqrt{\mathrm{3}}\:\:+\frac{\mathrm{6}}{\:\sqrt{\mathrm{3}}}\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{n}} \:{cos}\left({nx}\right)\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *