Menu Close

let-f-x-arctan-1-2x-1-calculate-f-n-x-then-f-n-0-2-developp-f-at-integr-serie-we-have-f-x-2-1-1-2x-2-f-n-x-2-1-2x-1-2-1-n-1-with-n-gt-0-let-W-x-

Tinku Tara 0 Comments
Pin




Question Number 53957 by maxmathsup by imad last updated on 05/Feb/19
let f(x) =arctan(1+2x) 1) calculate f^((n)) (x) then f^((n)) (0) 2) developp f at integr serie . we have f^′ (x)=(2/(1+(1+2x)^2 )) ⇒ f^((n)) (x) =2 {(1/((2x+1)^2 +1))}^((n−1)) with n>0 let W(x)=(1/((2x+1)^2 +1)) ⇒W(x) =(1/((2x+1+i)(2x+1−i))) =(1/(4(x+((1+i)/2))(x+((1−i)/2)))) =(1/(4(x +(1/( (√2))) e^((iπ)/4) )( x +(1/( (√2))) e^(−((iπ)/4)) ))) but ((1/(x +(1/( (√2)))e^(−((iπ)/4)) )) −(1/(x+(1/( (√2)))e^((iπ)/4) ))) =(1/( (√2))) (((2isin((π/4))))/((x+(1/( (√2)))e^(−((iπ)/4)) )(x+(1/( (√2)))e^((iπ)/4) ))) ⇒ W(x) =(1/(4i)){ (1/(x+(1/( (√2)))e^(−((iπ)/4)) )) −(1/(x+(1/( (√2)))e^((iπ)/4) ))} ⇒ W^((n−1)) (x)=(1/(4i)){ (((−1)^(n−1) (n−1)!)/((x+(1/( (√2)))e^(−((iπ)/4)) )^n )) −(((−1)^(n−1) (n−1)!)/((x+(1/( (√2)))e^((iπ)/4) )^n ))} ⇒ f^((n)) (x)=(((−1)^(n−1) (n−1)!)/(2i)){ (1/((x+(1/( (√2)))e^(−((iπ)/4)) )^n )) −(1/((x+(1/( (√2)))e^((iπ)/4) )^n ))} and f^((n)) (0) =(((−1)^(n−1) (n−1)!)/(2i)){ (1/( (√2))^(−n) e^(−i((nπ)/4)) )) −(1/(((√2))^(−n) e^(i((nπ)/4)) ))} =(((−1)^(n−1) (n−1)!)/(2i)){ ((√2))^n e^((inπ)/4) − ((√2))^n e^(−((inπ)/4)) } =(((−1)^(n−1) (n−1)!)/(2i)) ((√2))^n 2i sin(((nπ)/4)) =(−1)^(n−1) (n−1)! ((√2))^n sin(((nπ)/4))
$${let}\:{f}\left({x}\right)\:={arctan}\left(\mathrm{1}+\mathrm{2}{x}\right) \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}^{\left({n}\right)} \left({x}\right)\:{then}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie}\:. \\ $$$${we}\:{have}\:{f}^{'} \left({x}\right)=\frac{\mathrm{2}}{\mathrm{1}+\left(\mathrm{1}+\mathrm{2}{x}\right)^{\mathrm{2}} }\:\Rightarrow\:{f}^{\left({n}\right)} \left({x}\right)\:=\mathrm{2}\:\left\{\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\right\}^{\left({n}−\mathrm{1}\right)} \:\:{with}\:{n}>\mathrm{0} \\ $$$${let}\:{W}\left({x}\right)=\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow{W}\left({x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}+{i}\right)\left(\mathrm{2}{x}+\mathrm{1}−{i}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\left({x}+\frac{\mathrm{1}+{i}}{\mathrm{2}}\right)\left({x}+\frac{\mathrm{1}−{i}}{\mathrm{2}}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}\left({x}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left(\:{x}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}\:{but} \\ $$$$\left(\frac{\mathrm{1}}{{x}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} }\:−\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} }\right)\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\frac{\left(\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{4}}\right)\right)}{\left({x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)}\:\Rightarrow \\ $$$${W}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{4}{i}}\left\{\:\:\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} }\:−\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} }\right\}\:\Rightarrow \\ $$$${W}^{\left({n}−\mathrm{1}\right)} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}{i}}\left\{\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}} }\:−\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}} }\right\}\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\:\:\:\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}} }\:−\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}} }\right\}\:{and} \\ $$$${f}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\:\:\frac{\mathrm{1}}{\left.\:\sqrt{\mathrm{2}}\right)^{−{n}} \:{e}^{−{i}\frac{{n}\pi}{\mathrm{4}}} }\:−\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}\right)^{−{n}} \:{e}^{{i}\frac{{n}\pi}{\mathrm{4}}} }\right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\:\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{\frac{{in}\pi}{\mathrm{4}}} \:−\:\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{−\frac{{in}\pi}{\mathrm{4}}} \right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}{i}}\:\left(\sqrt{\mathrm{2}}\right)^{{n}} \:\mathrm{2}{i}\:{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)\:=\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\:\left(\sqrt{\mathrm{2}}\right)^{{n}} {sin}\left(\frac{{n}\pi}{\mathrm{4}}\right) \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 05/Feb/19
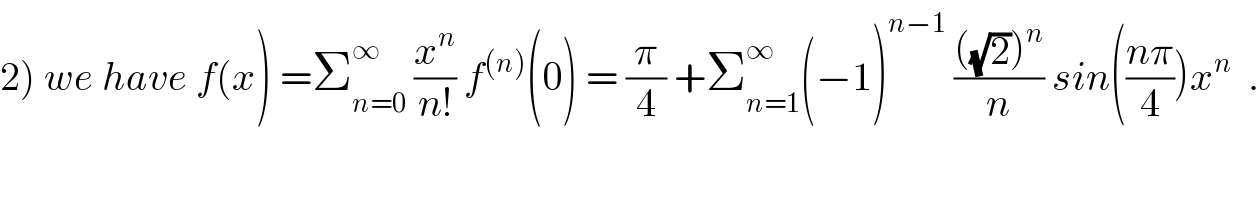
2) we have f(x) =Σ_(n=0) ^∞ (x^n /(n!)) f^((n)) (0) = (π/4) +Σ_(n=1) ^∞ (−1)^(n−1) ((((√2))^n )/n) sin(((nπ)/4))x^n .
$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{{n}} }{{n}!}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\:\frac{\pi}{\mathrm{4}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:\frac{\left(\sqrt{\mathrm{2}}\right)^{{n}} }{{n}}\:{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right){x}^{{n}} \:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *