Menu Close

let-f-x-arctan-2x-1-x-find-f-n-x-andf-n-1-

Tinku Tara 0 Comments
Pin




Question Number 83254 by mathmax by abdo last updated on 29/Feb/20
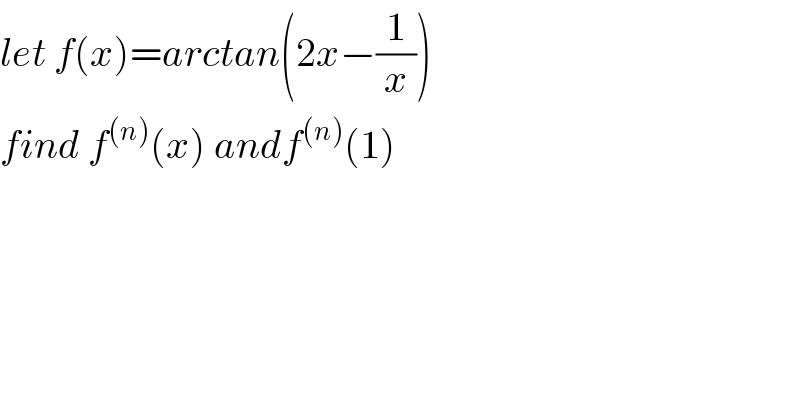
let f(x)=arctan(2x−(1/x)) find f^((n)) (x) andf^((n)) (1)
$${let}\:{f}\left({x}\right)={arctan}\left(\mathrm{2}{x}−\frac{\mathrm{1}}{{x}}\right) \\ $$$${find}\:{f}^{\left({n}\right)} \left({x}\right)\:{andf}^{\left({n}\right)} \left(\mathrm{1}\right) \\ $$
Commented by mathmax by abdo last updated on 02/Mar/20
we have f^′ (x)=((2+(1/x^2 ))/(1+(2x−(1/x))^2 )) =((2x^2 +1)/(x^2 {1+(((2x^2 −1)^2 )/x^2 )})) =((2x^2 +1)/(x^2 +(2x^2 −1)^2 )) =((2x^2 +1)/(x^2 +4x^4 −4x^2 +1)) =((2x^2 +1)/(4x^4 −3x^2 +1)) 4x^4 −3x^2 +1=0 →4t^2 −3t +1=0 (t=x^2 ) Δ=9−16 =−7 ⇒t_1 =((3+i(√7))/8) and t_2 =((3−i(√7))/8) ⇒ f^′ (x)=((2x^2 +1)/(4(x^2 −t_1 )(x^2 −t_2 ))) =(1/(4(t_1 −t_2 )))((1/(x^2 −t_1 ))−(1/(x^2 −t_2 )))(2x^2 +1) =(1/(i(√7))){ ((2x^2 +1)/(x^2 −t_1 ))−((2x^2 +1)/(x^2 −t_2 ))} =(1/(i(√7))){((2(x^2 −t_1 )+1+2t_1 )/(x^2 −t_1 ))−((2(x^2 −t_2 )+1+2t_2 )/(x^2 −t_2 ))} =(1/(i(√7))){((2t_1 +1)/(x^2 −t_1 ))−((2t_2 +1)/(x^2 −t_2 ))} =(1/(i(√7))){((2t_1 +1)/(2(√t_1 )))×((1/(x−(√t_1 )))−(1/(x+(√t_1 )))) −((2t_2 +1)/(2(√t_2 )))((1/(x−(√t_2 )))−(1/(x+(√t_2 ))))}⇒ f^((n)) (x) =((2t_1 +1)/(2i(√7)(√t_1 ))){ (((−1)^(n−1) (n−1)!)/((x−(√t_1 ))^n ))−(((−1)^(n−1) (n−1)!)/((x+(√t_1 ))^n ))} −((2t_2 +1)/(2i(√7)(√t_2 ))){ (((−1)^(n−1) (n−1)!)/((x−(√t_2 ))^n ))−(((−1)^(n−1) (n−1)!)/((x+(√t_2 ))^n ))} be continued..
$${we}\:{have}\:{f}^{'} \left({x}\right)=\frac{\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{1}+\left(\mathrm{2}{x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}{{x}^{\mathrm{2}} \left\{\mathrm{1}+\frac{\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right\}} \\ $$$$=\frac{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}{{x}^{\mathrm{2}} \:+\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{4}{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{4}{x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{4}{x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{1}=\mathrm{0}\:\rightarrow\mathrm{4}{t}^{\mathrm{2}} −\mathrm{3}{t}\:+\mathrm{1}=\mathrm{0}\:\:\:\left({t}={x}^{\mathrm{2}} \right) \\ $$$$\Delta=\mathrm{9}−\mathrm{16}\:=−\mathrm{7}\:\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{3}+{i}\sqrt{\mathrm{7}}}{\mathrm{8}}\:\:{and}\:{t}_{\mathrm{2}} =\frac{\mathrm{3}−{i}\sqrt{\mathrm{7}}}{\mathrm{8}}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)=\frac{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{4}\left({x}^{\mathrm{2}} −{t}_{\mathrm{1}} \right)\left({x}^{\mathrm{2}} −{t}_{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mathrm{4}\left({t}_{\mathrm{1}} −{t}_{\mathrm{2}} \right)}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{t}_{\mathrm{1}} }−\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{t}_{\mathrm{2}} }\right)\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{{i}\sqrt{\mathrm{7}}}\left\{\:\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{2}} −{t}_{\mathrm{1}} }−\frac{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}{{x}^{\mathrm{2}} −{t}_{\mathrm{2}} }\right\}\:=\frac{\mathrm{1}}{{i}\sqrt{\mathrm{7}}}\left\{\frac{\mathrm{2}\left({x}^{\mathrm{2}} −{t}_{\mathrm{1}} \right)+\mathrm{1}+\mathrm{2}{t}_{\mathrm{1}} }{{x}^{\mathrm{2}} −{t}_{\mathrm{1}} }−\frac{\mathrm{2}\left({x}^{\mathrm{2}} −{t}_{\mathrm{2}} \right)+\mathrm{1}+\mathrm{2}{t}_{\mathrm{2}} }{{x}^{\mathrm{2}} −{t}_{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{1}}{{i}\sqrt{\mathrm{7}}}\left\{\frac{\mathrm{2}{t}_{\mathrm{1}} +\mathrm{1}}{{x}^{\mathrm{2}} −{t}_{\mathrm{1}} }−\frac{\mathrm{2}{t}_{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{2}} −{t}_{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{1}}{{i}\sqrt{\mathrm{7}}}\left\{\frac{\mathrm{2}{t}_{\mathrm{1}} +\mathrm{1}}{\mathrm{2}\sqrt{{t}_{\mathrm{1}} }}×\left(\frac{\mathrm{1}}{{x}−\sqrt{{t}_{\mathrm{1}} }}−\frac{\mathrm{1}}{{x}+\sqrt{{t}_{\mathrm{1}} }}\right)\:−\frac{\mathrm{2}{t}_{\mathrm{2}} +\mathrm{1}}{\mathrm{2}\sqrt{{t}_{\mathrm{2}} }}\left(\frac{\mathrm{1}}{{x}−\sqrt{{t}_{\mathrm{2}} }}−\frac{\mathrm{1}}{{x}+\sqrt{{t}_{\mathrm{2}} }}\right)\right\}\Rightarrow \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\frac{\mathrm{2}{t}_{\mathrm{1}} +\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{7}}\sqrt{{t}_{\mathrm{1}} }}\left\{\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}−\sqrt{{t}_{\mathrm{1}} }\right)^{{n}} }−\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}+\sqrt{{t}_{\mathrm{1}} }\right)^{{n}} }\right\} \\ $$$$−\frac{\mathrm{2}{t}_{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{7}}\sqrt{{t}_{\mathrm{2}} }}\left\{\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}−\sqrt{{t}_{\mathrm{2}} }\right)^{{n}} }−\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}+\sqrt{{t}_{\mathrm{2}} }\right)^{{n}} }\right\}\:\:{be}\:{continued}.. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *