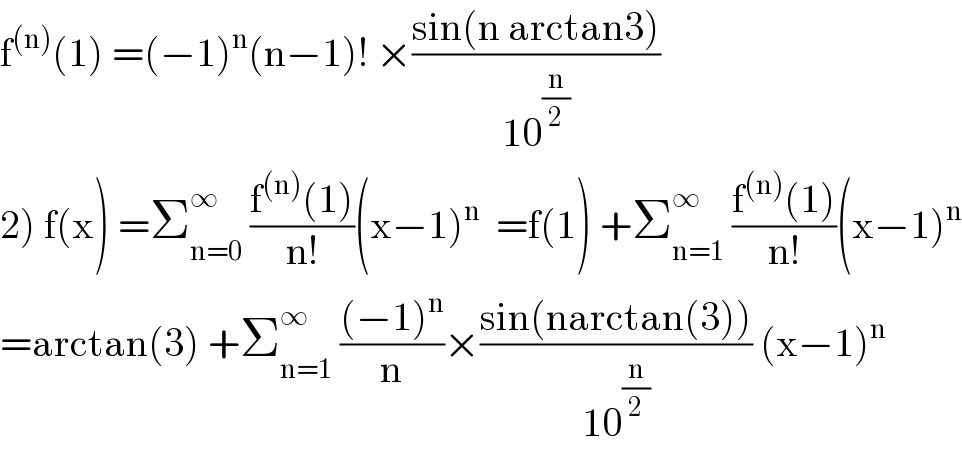Menu Close

let-f-x-arctan-3-x-1-calculste-f-n-x-and-f-n-1-2-developp-f-at-integr-seri-at-point-x-0-1-

Tinku Tara 0 Comments
Pin




Question Number 98722 by mathmax by abdo last updated on 15/Jun/20
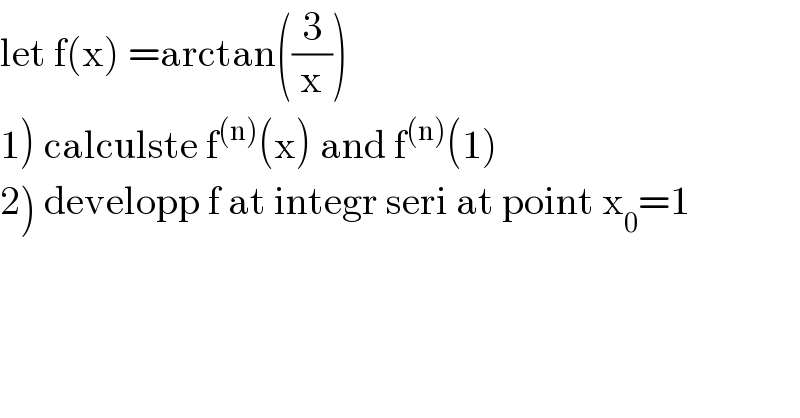
let f(x) =arctan((3/x)) 1) calculste f^((n)) (x) and f^((n)) (1) 2) developp f at integr seri at point x_0 =1
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right) \\ $$$$\left.\mathrm{1}\right)\:\mathrm{calculste}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{1}\right) \\ $$$$\left.\mathrm{2}\right)\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{integr}\:\mathrm{seri}\:\mathrm{at}\:\mathrm{point}\:\mathrm{x}_{\mathrm{0}} =\mathrm{1} \\ $$
Answered by MWSuSon last updated on 16/Jun/20
y=arctan((3/x)) y′=((−3)/((x^2 +9)))=(1/(2i))[(1/(x+3i))−(1/(x−3i))] y^(n+1) =(1/(2i))[n!(−1)^n (x+3i)^(−(n+1)) −n!(−1)^n (x−3i)^(−(n+1)) ] y^n =(1/(2i))[(n−1)!(−1)^(n−1) (x+3i)^(−n) −(n−1)!(−1)^(n−1) (x−3i)^(−n) ] can be further simplified... let x=rcosθ and 3=rsinθ y^n =(1/(2i))(n−1)!(−1)^(n−1) [(rcosθ+irsinθ)^(−n) −(rcosθ−irsinθ)^(−n) ] y^n =(1/(2i))(n−1)!(−1)^(n−1) r^(−n) [cosnθ−isinnθ−cosnθ−isinnθ] y^n =−(n−1)!(−1)^(n−1) r^(−n) ×sinnθ y^n =(n−1)!(−1)^n r^(−n) sinnθ [r=(√(x^2 +9))] [θ = arctan((3/x))] 2) y^n (1) = (n−1)!(−1)^n ((√(10)))^(−n) ×sinn(arctan(3))
$$\mathrm{y}=\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right) \\ $$$$\mathrm{y}'=\frac{−\mathrm{3}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{9}\right)}=\frac{\mathrm{1}}{\mathrm{2i}}\left[\frac{\mathrm{1}}{\mathrm{x}+\mathrm{3i}}−\frac{\mathrm{1}}{\mathrm{x}−\mathrm{3i}}\right] \\ $$$$\mathrm{y}^{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2i}}\left[\mathrm{n}!\left(−\mathrm{1}\right)^{{n}} \left(\mathrm{x}+\mathrm{3i}\right)^{−\left(\mathrm{n}+\mathrm{1}\right)} −\mathrm{n}!\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{x}−\mathrm{3i}\right)^{−\left(\mathrm{n}+\mathrm{1}\right)} \right] \\ $$$$\mathrm{y}^{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2i}}\left[\left(\mathrm{n}−\mathrm{1}\right)!\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \left(\mathrm{x}+\mathrm{3i}\right)^{−\mathrm{n}} −\left(\mathrm{n}−\mathrm{1}\right)!\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({x}−\mathrm{3}{i}\right)^{−{n}} \right] \\ $$$$\mathrm{can}\:\mathrm{be}\:\mathrm{further}\:\mathrm{simplified}… \\ $$$$\mathrm{let}\:\mathrm{x}=\mathrm{rcos}\theta\:\mathrm{and}\:\mathrm{3}=\mathrm{rsin}\theta \\ $$$$\mathrm{y}^{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2i}}\left(\mathrm{n}−\mathrm{1}\right)!\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \left[\left(\mathrm{rcos}\theta+\mathrm{irsin}\theta\right)^{−{n}} −\left(\mathrm{rcos}\theta−\mathrm{irsin}\theta\right)^{−\mathrm{n}} \right] \\ $$$$\mathrm{y}^{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2i}}\left(\mathrm{n}−\mathrm{1}\right)!\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{r}^{−\mathrm{n}} \left[\mathrm{cosn}\theta−\mathrm{isinn}\theta−\mathrm{cosn}\theta−\mathrm{isinn}\theta\right] \\ $$$$\mathrm{y}^{\mathrm{n}} =−\left(\mathrm{n}−\mathrm{1}\right)!\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{r}^{−\mathrm{n}} ×\mathrm{sinn}\theta \\ $$$$\mathrm{y}^{\mathrm{n}} =\left(\mathrm{n}−\mathrm{1}\right)!\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{r}^{−\mathrm{n}} \mathrm{sinn}\theta \\ $$$$\left[\mathrm{r}=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{9}}\right] \\ $$$$\left[\theta\:=\:\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)\right] \\ $$$$\left.\mathrm{2}\right)\:\mathrm{y}^{\mathrm{n}} \left(\mathrm{1}\right)\:=\:\left(\mathrm{n}−\mathrm{1}\right)!\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sqrt{\mathrm{10}}\right)^{−\mathrm{n}} ×\mathrm{sinn}\left(\mathrm{arctan}\left(\mathrm{3}\right)\right) \\ $$
Answered by MWSuSon last updated on 15/Jun/20
i don′t understand what your number 2 mean, sir please retype.
$$\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{what}\:\mathrm{your}\:\mathrm{number}\:\mathrm{2}\:\mathrm{mean}, \\ $$$$\mathrm{sir}\:\mathrm{please}\:\mathrm{retype}. \\ $$
Commented by mathmax by abdo last updated on 15/Jun/20
taylor serie at x_0 =1
$$\mathrm{taylor}\:\mathrm{serie}\:\mathrm{at}\:\mathrm{x}_{\mathrm{0}} =\mathrm{1} \\ $$
Commented by MWSuSon last updated on 15/Jun/20
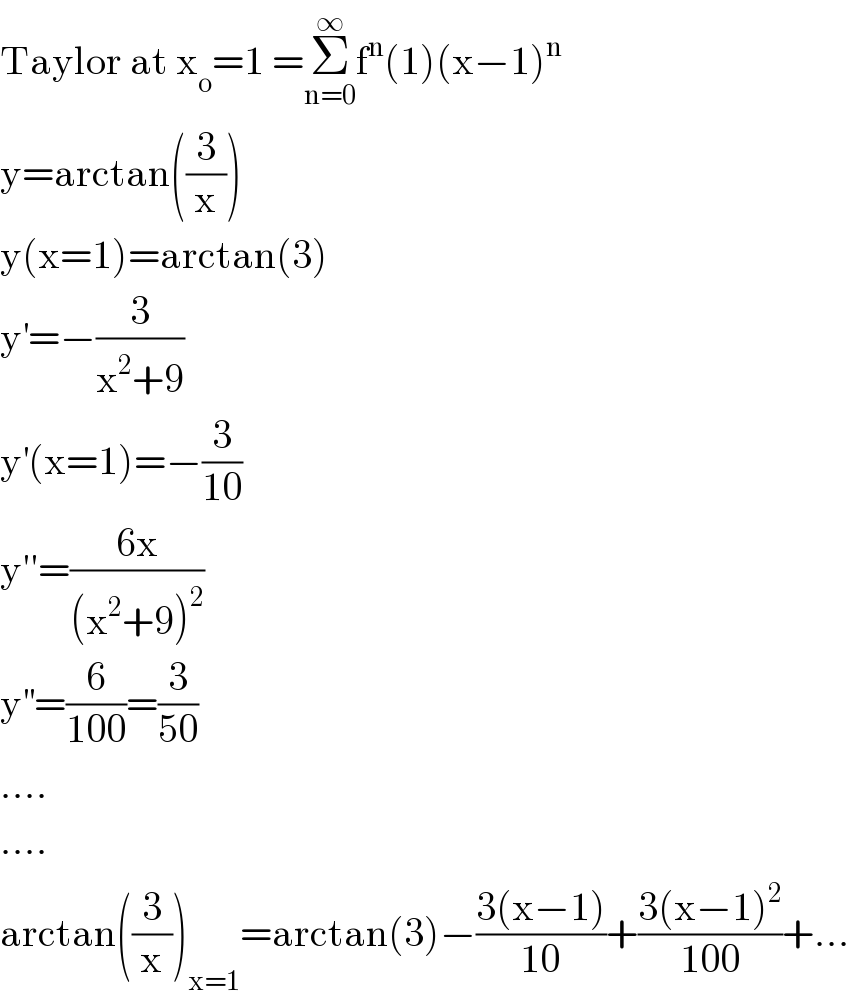
Taylor at x_o =1 =Σ_(n=0) ^∞ f^n (1)(x−1)^n y=arctan((3/x)) y(x=1)=arctan(3) y^′ =−(3/(x^2 +9)) y^′ (x=1)=−(3/(10)) y′′=((6x)/((x^2 +9)^2 )) y^(′′) =(6/(100))=(3/(50)) .... .... arctan((3/x))_(x=1) =arctan(3)−((3(x−1))/(10))+((3(x−1)^2 )/(100))+...
$$\mathrm{Taylor}\:\mathrm{at}\:\mathrm{x}_{\mathrm{o}} =\mathrm{1}\:=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{f}^{\mathrm{n}} \left(\mathrm{1}\right)\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{n}} \\ $$$$\mathrm{y}=\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right) \\ $$$$\mathrm{y}\left(\mathrm{x}=\mathrm{1}\right)=\mathrm{arctan}\left(\mathrm{3}\right) \\ $$$$\mathrm{y}^{'} =−\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} +\mathrm{9}} \\ $$$$\mathrm{y}^{'} \left(\mathrm{x}=\mathrm{1}\right)=−\frac{\mathrm{3}}{\mathrm{10}} \\ $$$$\mathrm{y}''=\frac{\mathrm{6x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} } \\ $$$$\mathrm{y}^{''} =\frac{\mathrm{6}}{\mathrm{100}}=\frac{\mathrm{3}}{\mathrm{50}} \\ $$$$…. \\ $$$$…. \\ $$$$\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)_{\mathrm{x}=\mathrm{1}} =\mathrm{arctan}\left(\mathrm{3}\right)−\frac{\mathrm{3}\left(\mathrm{x}−\mathrm{1}\right)}{\mathrm{10}}+\frac{\mathrm{3}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{100}}+… \\ $$
Answered by mathmax by abdo last updated on 15/Jun/20
1) f(x) =arctan((3/x)) ⇒f^′ (x) =((−3)/(x^2 (1+(9/x^2 )))) =((−3)/(x^2 +9)) =((−3)/((x−3i)(x+3i))) =−3((1/(x−3i))−(1/(x+3i)))×(1/(6i)) =−(1/(2i))((1/(x−3i))−(1/(x+3i))) ⇒ f^((n)) (x) =−(1/(2i)){ ((1/(x−3i)))^((n−1)) −((1/(x+3i)))^((n−1)) } (n≥1) f^((n)) (x) =(i/2){ (((−1)^(n−1) (n−1)!)/((x−3i)^n ))−(((−1)^(n−1) (n−1)!)/((x+3i)^n ))} =(i/2)(−1)^(n−1) (n−1)!{(((x+3i)^n −(x−3i)^n )/((x^2 +9)^n ))} =(i/2)(−1)^(n−1) (n−1)!×((2i Im(x+3i)^n )/((x^2 +9)^n )) =(−1)^n (n−1)!×((Im(x+3i)^n )/((x^2 +9)^n )) also we have x+3i =(√(x^2 +9))e^(iarctan((3/x))) ⇒ (x+3i)^n =(x^2 +9)^(n/2) e^(inarctan((3/x))) ⇒Im(x+3i)^n =(x^2 +9)^(n/2) sin(narctan((3/x))) ⇒ f^((n)) (x) =(−1)^n (n−1)!×((sin(narctan((3/x))))/((x^2 +9)^(n/2) ))
$$\left.\mathrm{1}\right)\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)\:=\frac{−\mathrm{3}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{9}}{\mathrm{x}^{\mathrm{2}} }\right)}\:=\frac{−\mathrm{3}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}} \\ $$$$=\frac{−\mathrm{3}}{\left(\mathrm{x}−\mathrm{3i}\right)\left(\mathrm{x}+\mathrm{3i}\right)}\:=−\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{3i}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{3i}}\right)×\frac{\mathrm{1}}{\mathrm{6i}}\:=−\frac{\mathrm{1}}{\mathrm{2i}}\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{3i}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{3i}}\right)\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=−\frac{\mathrm{1}}{\mathrm{2i}}\left\{\:\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{3i}}\right)^{\left(\mathrm{n}−\mathrm{1}\right)} −\left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{3i}}\right)^{\left(\mathrm{n}−\mathrm{1}\right)} \right\}\:\:\:\left(\mathrm{n}\geqslant\mathrm{1}\right) \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\frac{\mathrm{i}}{\mathrm{2}}\left\{\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \left(\mathrm{n}−\mathrm{1}\right)!}{\left(\mathrm{x}−\mathrm{3i}\right)^{\mathrm{n}} }−\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \left(\mathrm{n}−\mathrm{1}\right)!}{\left(\mathrm{x}+\mathrm{3i}\right)^{\mathrm{n}} }\right\} \\ $$$$=\frac{\mathrm{i}}{\mathrm{2}}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \left(\mathrm{n}−\mathrm{1}\right)!\left\{\frac{\left(\mathrm{x}+\mathrm{3i}\right)^{\mathrm{n}} −\left(\mathrm{x}−\mathrm{3i}\right)^{\mathrm{n}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{n}} }\right\} \\ $$$$=\frac{\mathrm{i}}{\mathrm{2}}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \left(\mathrm{n}−\mathrm{1}\right)!×\frac{\mathrm{2i}\:\:\mathrm{Im}\left(\mathrm{x}+\mathrm{3i}\right)^{\mathrm{n}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{n}} } \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{n}} \:\left(\mathrm{n}−\mathrm{1}\right)!×\frac{\mathrm{Im}\left(\mathrm{x}+\mathrm{3i}\right)^{\mathrm{n}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{n}} }\:\:\:\mathrm{also}\:\mathrm{we}\:\mathrm{have}\:\mathrm{x}+\mathrm{3i}\:=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{9}}\mathrm{e}^{\mathrm{iarctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)} \:\Rightarrow \\ $$$$\left(\mathrm{x}+\mathrm{3i}\right)^{\mathrm{n}} \:=\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\frac{\mathrm{n}}{\mathrm{2}}} \:\mathrm{e}^{\mathrm{inarctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)} \:\Rightarrow\mathrm{Im}\left(\mathrm{x}+\mathrm{3i}\right)^{\mathrm{n}} \:=\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\frac{\mathrm{n}}{\mathrm{2}}} \:\mathrm{sin}\left(\mathrm{narctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)\right)\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{n}−\mathrm{1}\right)!×\frac{\mathrm{sin}\left(\mathrm{narctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\frac{\mathrm{n}}{\mathrm{2}}} } \\ $$
Commented by mathmax by abdo last updated on 15/Jun/20
f^((n)) (1) =(−1)^n (n−1)! ×((sin(n arctan3))/(10^(n/2) )) 2) f(x) =Σ_(n=0) ^∞ ((f^((n)) (1))/(n!))(x−1)^n =f(1) +Σ_(n=1) ^∞ ((f^((n)) (1))/(n!))(x−1)^n =arctan(3) +Σ_(n=1) ^∞ (((−1)^n )/n)×((sin(narctan(3)))/(10^(n/2) )) (x−1)^n
$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{1}\right)\:=\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{n}−\mathrm{1}\right)!\:×\frac{\mathrm{sin}\left(\mathrm{n}\:\mathrm{arctan3}\right)}{\mathrm{10}^{\frac{\mathrm{n}}{\mathrm{2}}} } \\ $$$$\left.\mathrm{2}\right)\:\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{1}\right)}{\mathrm{n}!}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{n}} \:\:=\mathrm{f}\left(\mathrm{1}\right)\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{1}\right)}{\mathrm{n}!}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{n}} \\ $$$$=\mathrm{arctan}\left(\mathrm{3}\right)\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}×\frac{\mathrm{sin}\left(\mathrm{narctan}\left(\mathrm{3}\right)\right)}{\mathrm{10}^{\frac{\mathrm{n}}{\mathrm{2}}} }\:\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{n}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *