Question Number 36177 by prof Abdo imad last updated on 30/May/18
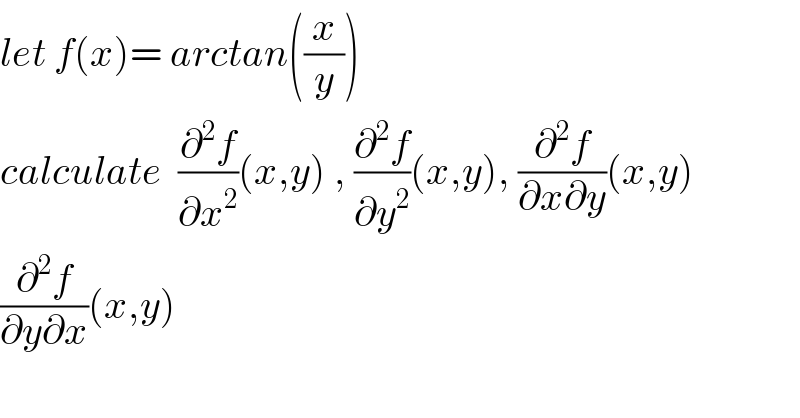
$${let}\:{f}\left({x}\right)=\:{arctan}\left(\frac{{x}}{{y}}\right) \\ $$$${calculate}\:\:\frac{\partial^{\mathrm{2}} {f}}{\partial{x}^{\mathrm{2}} }\left({x},{y}\right)\:,\:\frac{\partial^{\mathrm{2}} {f}}{\partial{y}^{\mathrm{2}} }\left({x},{y}\right),\:\frac{\partial^{\mathrm{2}} {f}}{\partial{x}\partial{y}}\left({x},{y}\right) \\ $$$$\frac{\partial^{\mathrm{2}} {f}}{\partial{y}\partial{x}}\left({x},{y}\right) \\ $$
Commented by maxmathsup by imad last updated on 19/Aug/18

$${we}\:{have}\:\frac{\partial{f}}{\partial{x}}\left({x},{y}\right)\:=\:\:\frac{\mathrm{1}}{{y}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }\right)}\:=\:\frac{\mathrm{1}}{{y}\:+\frac{{x}^{\mathrm{2}} }{{y}}}\:=\:\frac{{y}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\partial^{\mathrm{2}} {f}}{\partial{x}^{\mathrm{2}} }\left({x},{y}\right)\:=\frac{\partial}{\partial{x}}\left\{\:\:\frac{{y}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\right\}\:={y}.\frac{−\mathrm{2}{x}}{\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{−\mathrm{2}{xy}}{\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:{also}\:{we}\:{have} \\ $$$$\frac{\partial{f}}{\partial{y}}\left({x},{y}\right)\:=\frac{−{x}}{{y}^{\mathrm{2}} \left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }\right)}\:\:=\frac{−{x}}{{y}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\partial^{\mathrm{2}} {f}}{\partial{y}^{\mathrm{2}} }\left({x},{y}\right)\:=\frac{\partial}{\partial{y}}\left\{\:\frac{−{x}}{{y}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\right\}\:=−{x}\:\frac{−\mathrm{2}{y}}{\left({y}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{\mathrm{2}{xy}}{\left({y}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:{also} \\ $$$$\frac{\partial^{\mathrm{2}} {f}}{\partial{y}\partial{x}}\left({x},{y}\right)\:=\frac{\partial}{\partial{y}}\left(\frac{\partial{f}}{\partial{x}}\left({x},{y}\right)\right)=\frac{\partial}{\partial{y}}\left\{\frac{{y}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\right\}=\frac{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:−{y}\left(\mathrm{2}{y}\right)}{\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{{x}^{\mathrm{2}} \:−{y}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:{also} \\ $$$$\frac{\partial^{\mathrm{2}} {f}}{\partial{x}\partial{y}}\left({x},{y}\right)\:=\:\frac{\partial}{\partial{x}}\left(\frac{\partial{f}}{\partial{y}}\left({x},{y}\right)\right)\:=\frac{\partial}{\partial{x}}\left\{\:\frac{−{x}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\right\}\:=\frac{−\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)+{x}\left(\mathrm{2}{x}\right)}{\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{{x}^{\mathrm{2}} \:−{y}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\mathrm{2}} }\:. \\ $$$$ \\ $$
