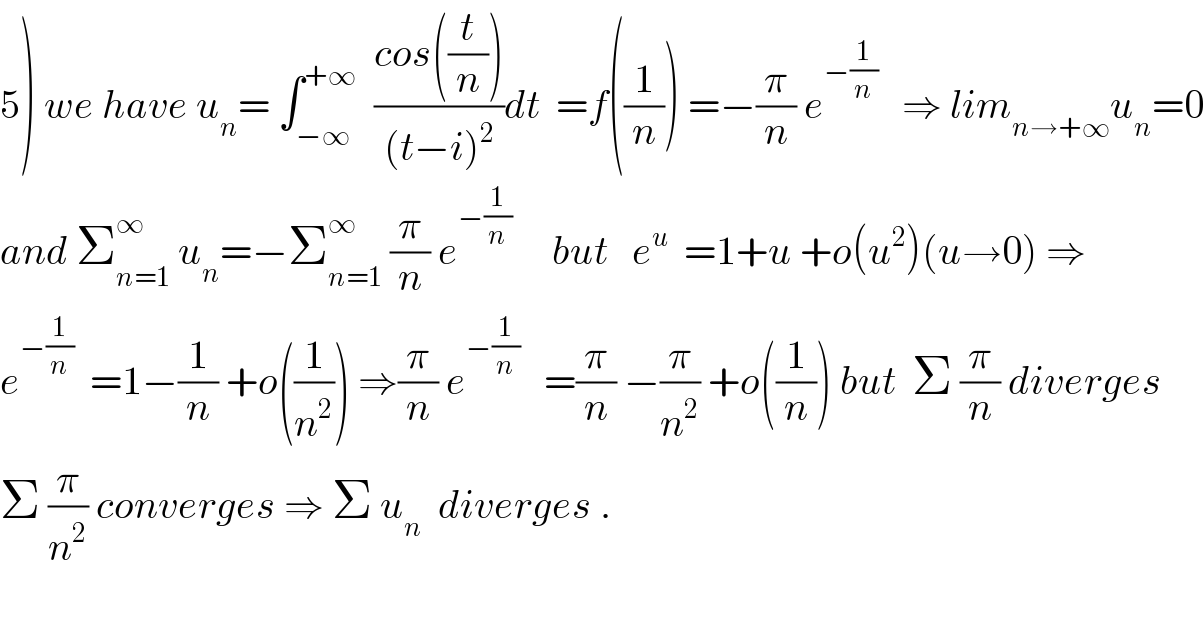Question Number 42305 by maxmathsup by imad last updated on 22/Aug/18
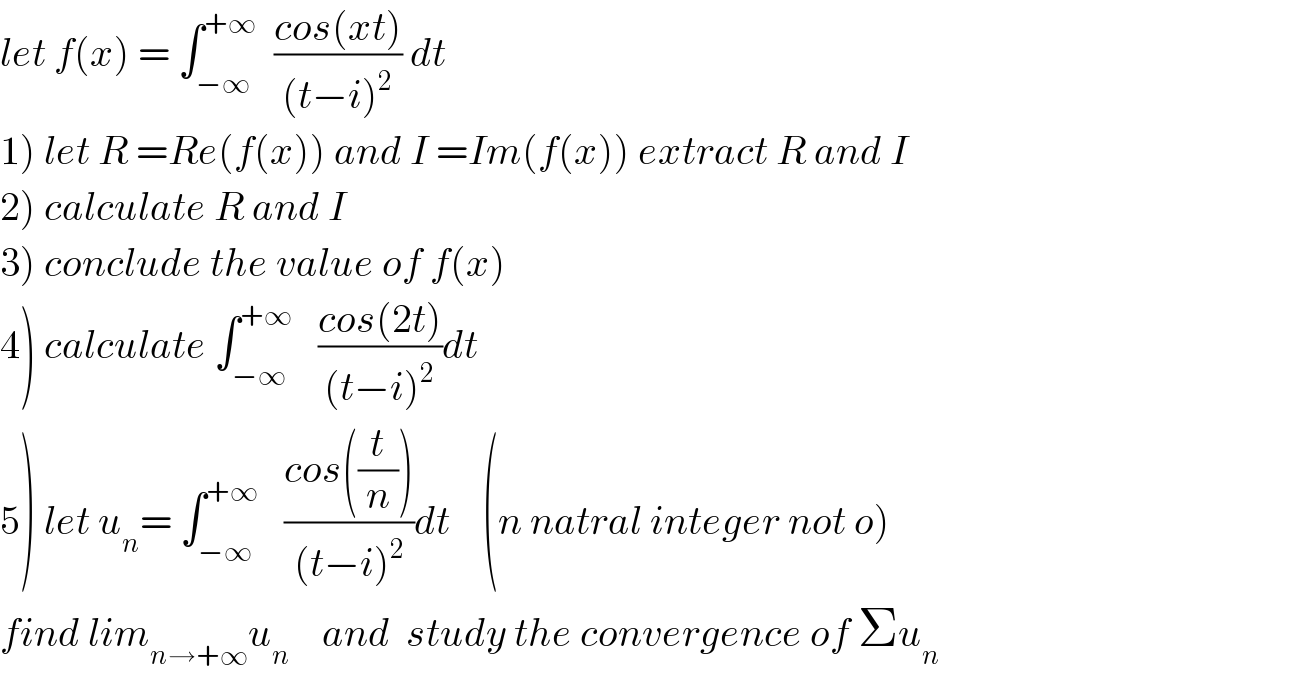
Commented by maxmathsup by imad last updated on 22/Aug/18

Commented by maxmathsup by imad last updated on 23/Aug/18
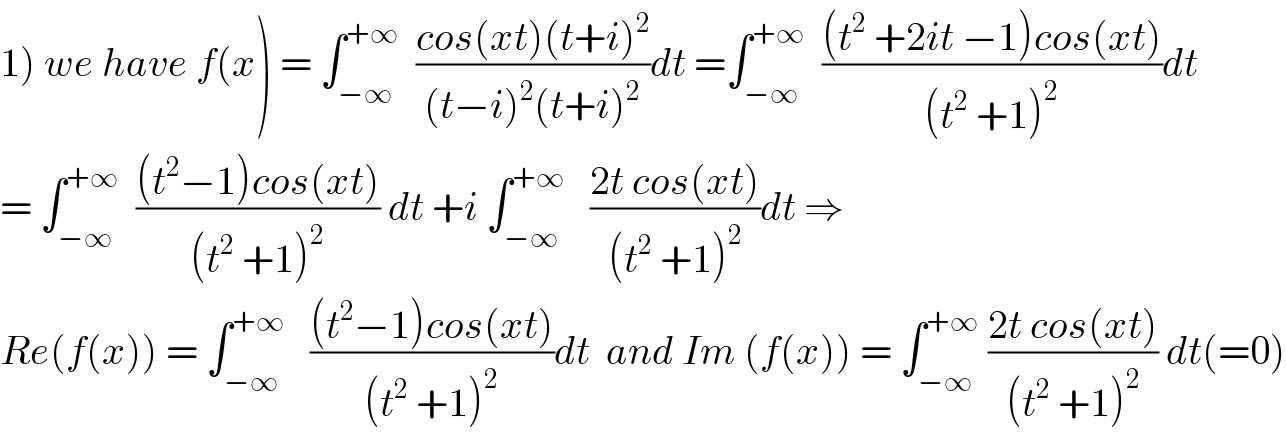
Commented by maxmathsup by imad last updated on 23/Aug/18
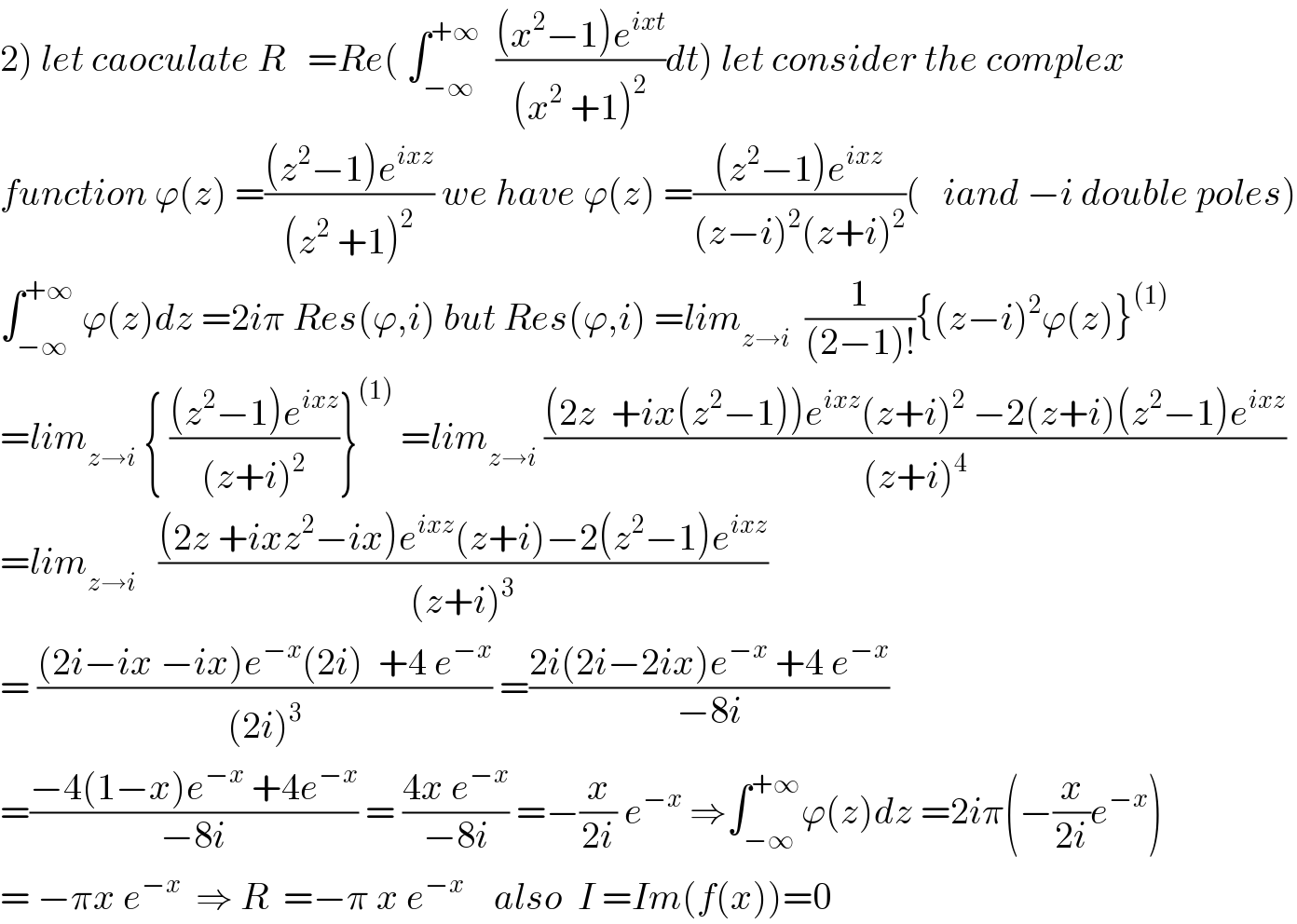
Commented by maxmathsup by imad last updated on 23/Aug/18
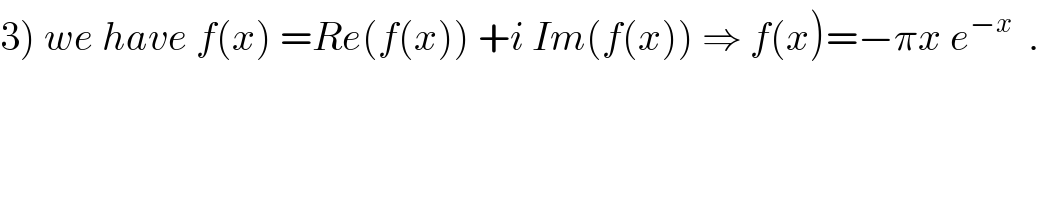
Commented by maxmathsup by imad last updated on 23/Aug/18
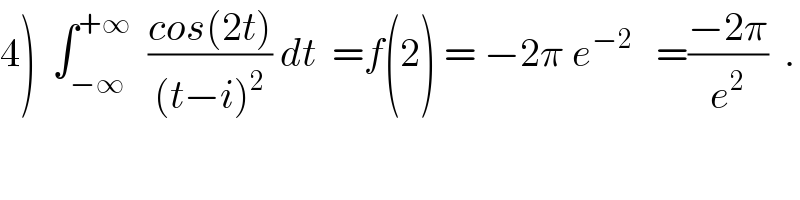
Commented by maxmathsup by imad last updated on 23/Aug/18