Menu Close

let-f-x-cosx-cos-2x-cos-3x-1-calculate-f-n-x-and-f-n-0-2-developp-f-at-integr-serie-3-calculate-0-pi-2-f-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 101500 by mathmax by abdo last updated on 03/Jul/20
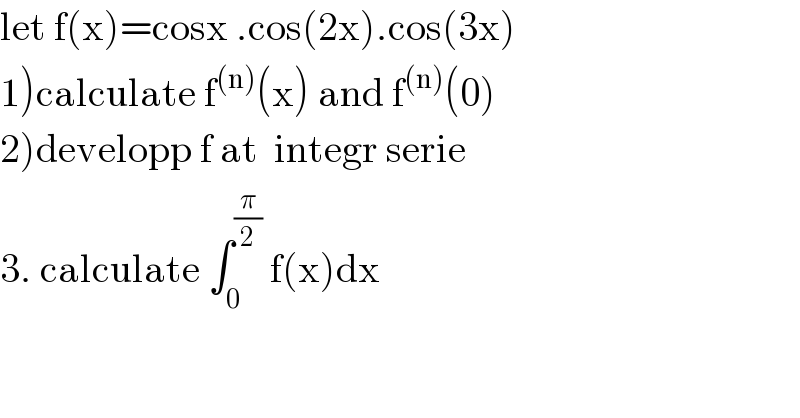
let f(x)=cosx .cos(2x).cos(3x) 1)calculate f^((n)) (x) and f^((n)) (0) 2)developp f at integr serie 3. calculate ∫_0 ^(π/2) f(x)dx
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{cosx}\:.\mathrm{cos}\left(\mathrm{2x}\right).\mathrm{cos}\left(\mathrm{3x}\right) \\ $$$$\left.\mathrm{1}\right)\mathrm{calculate}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\:\mathrm{integr}\:\mathrm{serie} \\ $$$$\mathrm{3}.\:\mathrm{calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$
Commented by bemath last updated on 03/Jul/20
(3)∫_0 ^(π/2) f(x) dx =[(1/4)x+(1/(24))sin 6x+ (1/8)sin 2x+(1/(16))sin 4x ]_0 ^(π/2) = (π/8) ■ cos (3x)cos (x)cos (2x)= (1/2)(cos 4x+cos 2x)cos 2x= (1/2)(cos 4xcos 2x+cos^2 2x)= (1/2)((1/2)(cos 6x+cos 2x)+(1/2)+(1/2)cos 4x)= (1/4)cos 6x+(1/4)cos 2x+(1/4)+(1/4)cos 4x
$$\left(\mathrm{3}\right)\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{dx}\:=\left[\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}+\frac{\mathrm{1}}{\mathrm{24}}\mathrm{sin}\:\mathrm{6x}+\right. \\ $$$$\left.\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\:\mathrm{2x}+\frac{\mathrm{1}}{\mathrm{16}}\mathrm{sin}\:\mathrm{4x}\:\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$=\:\frac{\pi}{\mathrm{8}}\:\blacksquare \\ $$$$\mathrm{cos}\:\left(\mathrm{3x}\right)\mathrm{cos}\:\left(\mathrm{x}\right)\mathrm{cos}\:\left(\mathrm{2x}\right)= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\mathrm{4x}+\mathrm{cos}\:\mathrm{2x}\right)\mathrm{cos}\:\mathrm{2x}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\mathrm{4xcos}\:\mathrm{2x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x}\right)= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\mathrm{6x}+\mathrm{cos}\:\mathrm{2x}\right)+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{4x}\right)= \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{6x}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{2x}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{4x} \\ $$
Answered by Ramajunan last updated on 03/Jul/20
Nice question Expressing f(x) as the sum of cosines angles cosxcos(2x)cos(3x) ⇒(1/4)(cos(5x)+cosx)cosx ⇒(1/2)cos(5x)cosx+(1/2)cos^2 x ⇒f(x)=(1/4)[cos(6x)+cos(4x)+cos(2x)+1] f^′ (x)=(1/4)[−6sin(6x)−4sin(4x)−2sin(2x)] f^” (x)=(1/4)(−6^2 cos(6x)−4^2 cos(4x)−2^2 cos(2x)] f^((3)) (x)=(1/4)(6^3 sin(6x)+4^3 sin(x)+2^3 sin(2x) f^((n)) (x)=(1/4)(6^n cos(6x+((nπ)/2))+4^n cos(4x+((nπ)/2))+2^n cos(2x+((nπ)/2))] for ∨n f^n (0)=(1/4)(6^n cos(((nπ)/2))+4^n cos(((nπ)/2))+2^n cos(((nπ)/2))) =(1/4)(6^n +4^n +2^n )cos(((nπ)/2)) 2) Don′t understand number 2 Number 3 ∫_0 ^(π/2) cosxcos(2x)cos(3x)dx ∫_0 ^(π/2) f(x)=(1/4)∫_0 ^(π/2) [cos(6x)+cos(4x)+cos(2x)+1] [(1/4)(((sin(6x))/6)+((cos(4x))/4)+((sin(2x))/2)+x)]_0 ^(π/2)
$$\mathrm{Nice}\:\mathrm{question} \\ $$$$\mathrm{Expressing}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{as}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{cosines}\:\mathrm{angles} \\ $$$$\mathrm{cosxcos}\left(\mathrm{2x}\right)\mathrm{cos}\left(\mathrm{3x}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{cos}\left(\mathrm{5x}\right)+\mathrm{cosx}\right)\mathrm{cosx} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{5x}\right)\mathrm{cosx}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} \mathrm{x} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{cos}\left(\mathrm{6x}\right)+\mathrm{cos}\left(\mathrm{4x}\right)+\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{1}\right] \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left[−\mathrm{6sin}\left(\mathrm{6x}\right)−\mathrm{4sin}\left(\mathrm{4x}\right)−\mathrm{2sin}\left(\mathrm{2x}\right)\right] \\ $$$$\mathrm{f}^{''} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(−\mathrm{6}^{\mathrm{2}} \mathrm{cos}\left(\mathrm{6x}\right)−\mathrm{4}^{\mathrm{2}} \mathrm{cos}\left(\mathrm{4x}\right)−\mathrm{2}^{\mathrm{2}} \mathrm{cos}\left(\mathrm{2x}\right)\right] \\ $$$$\mathrm{f}^{\left(\mathrm{3}\right)} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{6}^{\mathrm{3}} \mathrm{sin}\left(\mathrm{6x}\right)+\mathrm{4}^{\mathrm{3}} \mathrm{sin}\left(\mathrm{x}\right)+\mathrm{2}^{\mathrm{3}} \mathrm{sin}\left(\mathrm{2x}\right)\right. \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{6}^{\mathrm{n}} \mathrm{cos}\left(\mathrm{6x}+\frac{{n}\pi}{\mathrm{2}}\right)+\mathrm{4}^{\mathrm{n}} \mathrm{cos}\left(\mathrm{4x}+\frac{\mathrm{n}\pi}{\mathrm{2}}\right)+\mathrm{2}^{{n}} {cos}\left(\mathrm{2}{x}+\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\right]\:\mathrm{for}\:\vee{n} \\ $$$$\mathrm{f}^{\mathrm{n}} \left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{6}^{\mathrm{n}} \mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)+\mathrm{4}^{\mathrm{n}} \mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)+\mathrm{2}^{{n}} \mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{6}^{\mathrm{n}} +\mathrm{4}^{\mathrm{n}} +\mathrm{2}^{\mathrm{n}} \right)\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:{Don}'{t}\:\mathrm{understand}\:\mathrm{number}\:\mathrm{2} \\ $$$$ \\ $$$$\mathrm{Number}\:\mathrm{3} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cosxcos}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{3}{x}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left[\mathrm{cos}\left(\mathrm{6x}\right)+\mathrm{cos}\left(\mathrm{4x}\right)+\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{1}\right] \\ $$$$\left[\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{sin}\left(\mathrm{6x}\right)}{\mathrm{6}}+\frac{\mathrm{cos}\left(\mathrm{4x}\right)}{\mathrm{4}}+\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}}+\mathrm{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$ \\ $$$$ \\ $$
Commented by abdomathmax last updated on 03/Jul/20
thanks sir.
$$\mathrm{thanks}\:\mathrm{sir}. \\ $$
Answered by mathmax by abdo last updated on 04/Jul/20
1) let transform f(x) to sum we have f(x) =cosx cos(2x).cos(3x) =(1/2){cos(3x)+cosx}cos(3x) =(1/2)cos^2 (3x)+(1/2) cosx cos(3x) =(1/4)(1+cos(6x))+(1/4){cos(4x)+cos(2x)} =(1/4)(1+cos(2x)+cos(4x) +cos(6x)} so for n≥1 we get f^((n)) (x) =(1/4){ cos^((n)) (2x)+cos^((n)) (4x) +cos^((n)) (6x)} =(1/4){ (((e^(2ix) +e^(−2ix) )/2))^((n)) +(((e^(4ix) +e^(−4ix) )/2))^((n) ) +(((e^(6ix) +e^(−6ix) )/2))^((n)) } =(1/8){ (2i)^n e^(2ix) +(−2i)^n e^(−2ix) +(4i)^n e^(4ix) +(−4i)^n e^(−4ix) +(6i)^n e^(6ix) +(−6i)^n e^(−6ix) } ⇒f^((n)) (0) =(1/8){ (2i)^(n ) +(−2i)^n +(4i)^n +(−4i)^(n ) +(6i)^n +(−6i)^n } =(1/8){ 2^n (i^(n ) +(−i)^n )+4^n (i^(n ) +(−i)^n ) +6^n (i^(n ) +(−i)^n )} =(1/8){2^n (2 cos(((nπ)/2))) +4^n (2cos(((nπ)/2)))+6^n (2cos(((nπ)/2))} f^((n)) (0)=(1/4)cos(((nπ)/2)){ 2^n +4^n +6^n }
$$\left.\mathrm{1}\right)\:\mathrm{let}\:\mathrm{transform}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{to}\:\mathrm{sum}\:\mathrm{we}\:\mathrm{have}\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{cosx}\:\mathrm{cos}\left(\mathrm{2x}\right).\mathrm{cos}\left(\mathrm{3x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{cos}\left(\mathrm{3x}\right)+\mathrm{cosx}\right\}\mathrm{cos}\left(\mathrm{3x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} \left(\mathrm{3x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{cosx}\:\mathrm{cos}\left(\mathrm{3x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{6x}\right)\right)+\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{cos}\left(\mathrm{4x}\right)+\mathrm{cos}\left(\mathrm{2x}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{cos}\left(\mathrm{4x}\right)\:+\mathrm{cos}\left(\mathrm{6x}\right)\right\}\:\mathrm{so}\:\mathrm{for}\:\mathrm{n}\geqslant\mathrm{1}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\:\mathrm{cos}^{\left(\mathrm{n}\right)} \left(\mathrm{2x}\right)+\mathrm{cos}^{\left(\mathrm{n}\right)} \left(\mathrm{4x}\right)\:+\mathrm{cos}^{\left(\mathrm{n}\right)} \left(\mathrm{6x}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{\:\left(\frac{\mathrm{e}^{\mathrm{2ix}} +\mathrm{e}^{−\mathrm{2ix}} }{\mathrm{2}}\right)^{\left(\mathrm{n}\right)} \:+\left(\frac{\mathrm{e}^{\mathrm{4ix}} +\mathrm{e}^{−\mathrm{4ix}} }{\mathrm{2}}\right)^{\left(\mathrm{n}\right)\:} \:+\left(\frac{\mathrm{e}^{\mathrm{6ix}} \:+\mathrm{e}^{−\mathrm{6ix}} }{\mathrm{2}}\right)^{\left(\mathrm{n}\right)} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left\{\:\:\left(\mathrm{2i}\right)^{\mathrm{n}} \:\mathrm{e}^{\mathrm{2ix}} \:+\left(−\mathrm{2i}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{2ix}} \:+\left(\mathrm{4i}\right)^{\mathrm{n}} \:\mathrm{e}^{\mathrm{4ix}} \:+\left(−\mathrm{4i}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{4ix}} \:+\left(\mathrm{6i}\right)^{\mathrm{n}} \:\mathrm{e}^{\mathrm{6ix}} \:+\left(−\mathrm{6i}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{6ix}} \right\} \\ $$$$\Rightarrow\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)\:=\frac{\mathrm{1}}{\mathrm{8}}\left\{\:\left(\mathrm{2i}\right)^{\mathrm{n}\:} \:+\left(−\mathrm{2i}\right)^{\mathrm{n}} \:+\left(\mathrm{4i}\right)^{\mathrm{n}} +\left(−\mathrm{4i}\right)^{\mathrm{n}\:} \:+\left(\mathrm{6i}\right)^{\mathrm{n}} \:+\left(−\mathrm{6i}\right)^{\mathrm{n}} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left\{\:\mathrm{2}^{\mathrm{n}} \left(\mathrm{i}^{\mathrm{n}\:} +\left(−\mathrm{i}\right)^{\mathrm{n}} \right)+\mathrm{4}^{\mathrm{n}} \left(\mathrm{i}^{\mathrm{n}\:} +\left(−\mathrm{i}\right)^{\mathrm{n}} \right)\:+\mathrm{6}^{\mathrm{n}} \left(\mathrm{i}^{\mathrm{n}\:} +\left(−\mathrm{i}\right)^{\mathrm{n}} \right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left\{\mathrm{2}^{\mathrm{n}} \left(\mathrm{2}\:\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\right)\:+\mathrm{4}^{\mathrm{n}} \left(\mathrm{2cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\right)+\mathrm{6}^{\mathrm{n}} \left(\mathrm{2cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\right\}\right. \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\left\{\:\mathrm{2}^{\mathrm{n}} \:+\mathrm{4}^{\mathrm{n}} \:+\mathrm{6}^{\mathrm{n}} \right\} \\ $$
Commented by mathmax by abdo last updated on 04/Jul/20
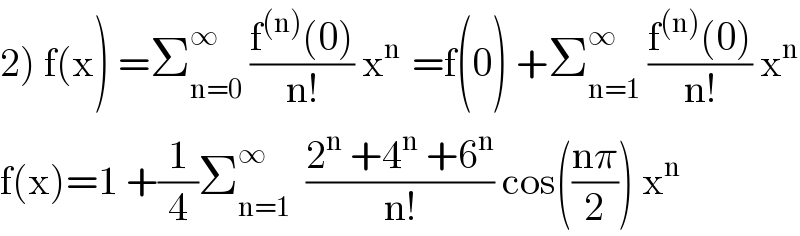
2) f(x) =Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^(n ) =f(0) +Σ_(n=1) ^∞ ((f^((n)) (0))/(n!)) x^n f(x)=1 +(1/4)Σ_(n=1) ^(∞ ) ((2^n +4^n +6^n )/(n!)) cos(((nπ)/2)) x^n
$$\left.\mathrm{2}\right)\:\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)}{\mathrm{n}!}\:\mathrm{x}^{\mathrm{n}\:} \:=\mathrm{f}\left(\mathrm{0}\right)\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)}{\mathrm{n}!}\:\mathrm{x}^{\mathrm{n}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{4}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty\:} \:\:\frac{\mathrm{2}^{\mathrm{n}} \:+\mathrm{4}^{\mathrm{n}} \:+\mathrm{6}^{\mathrm{n}} }{\mathrm{n}!}\:\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\:\mathrm{x}^{\mathrm{n}} \\ $$
Commented by mathmax by abdo last updated on 04/Jul/20
3) we have f(x) =(1/4){1+cos(2x)+cos(4x) +cos(6x)} ⇒ ∫_0 ^(π/2) f(x)dx =(π/8) +(1/4)∫_0 ^(π/2) cos(2x)dx +(1/4)∫_0 ^(π/2) cos(4x)dx +(1/4) ∫_0 ^(π/2) cos(6x)dx =(π/8) +(1/8)[sin(2x)]_0 ^(π/2) +(1/(16))[sin(4x)]_0 ^(π/2) +(1/(24))[sin(6x)]_0 ^(π/2) =(π/8) +0 +0 +0 =(π/8) ⇒ ∫_0 ^(π/2) f(x)dx =(π/8)
$$\left.\mathrm{3}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{cos}\left(\mathrm{4x}\right)\:+\mathrm{cos}\left(\mathrm{6x}\right)\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{dx}\:+\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{dx}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}\left(\mathrm{6x}\right)\mathrm{dx} \\ $$$$=\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{8}}\left[\mathrm{sin}\left(\mathrm{2x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:+\frac{\mathrm{1}}{\mathrm{16}}\left[\mathrm{sin}\left(\mathrm{4x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:+\frac{\mathrm{1}}{\mathrm{24}}\left[\mathrm{sin}\left(\mathrm{6x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\pi}{\mathrm{8}}\:+\mathrm{0}\:+\mathrm{0}\:+\mathrm{0}\:=\frac{\pi}{\mathrm{8}}\:\Rightarrow\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\frac{\pi}{\mathrm{8}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *