Menu Close

let-f-x-e-x-1-x-sin-3x-1-dtermine-f-n-x-and-f-n-0-2-developp-f-at-integr-serie-

Tinku Tara 0 Comments
Pin




Question Number 61329 by maxmathsup by imad last updated on 01/Jun/19
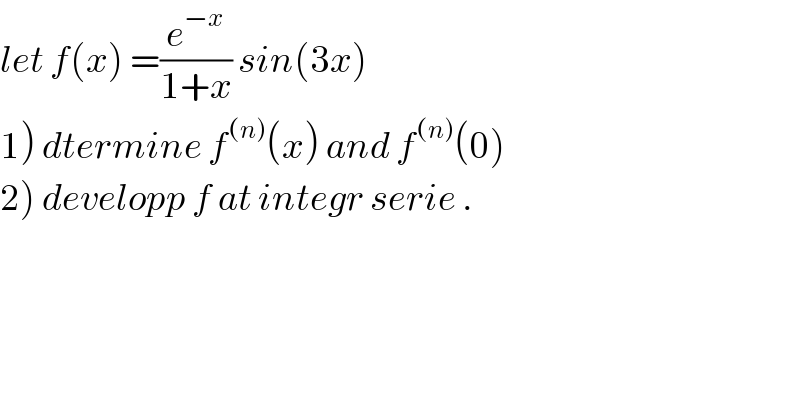
let f(x) =(e^(−x) /(1+x)) sin(3x) 1) dtermine f^((n)) (x) and f^((n)) (0) 2) developp f at integr serie .
$${let}\:{f}\left({x}\right)\:=\frac{{e}^{−{x}} }{\mathrm{1}+{x}}\:{sin}\left(\mathrm{3}{x}\right) \\ $$$$\left.\mathrm{1}\right)\:{dtermine}\:{f}^{\left({n}\right)} \left({x}\right)\:{and}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie}\:. \\ $$
Commented by maxmathsup by imad last updated on 03/Jun/19
1) we have f(x)=Im((1/(1+x))e^(−x+3ix) ) = Im((1/(1+x)) e^((−1+3i)x) )=Im(w(x)) we have w(x)^((n)) ={(1/(1+x)) e^((−1+3i)x) }^((n)) =_(leibniz) Σ_(k=0) ^n C_n ^k ((1/(1+x)))^((k)) (e^((−1+3i)x) )^((n−k)) but (e^(zx) )^((k)) =_(zfixed) z^k e^(zx) ⇒{e^((−1+3i)x) }^((n−k)) =(−1+3i)^(n−k) e^((−1+3i)x) also ((1/(1+x)))^((k)) =(((−1)^k k!)/((1+x)^(k+1) )) ⇒w^((n)) (x) = Σ_(k=0) ^n C_n ^k (((−1)^k k!)/((1+x)^(k+1) )) (−1+3i)^(n−k) e^((−1+3i)x) we have ∣−1+3i∣ =(√(1+9))=(√(10)) ⇒−1+3i =(√(10))(((−1)/( (√(10)))) +((3i)/( (√(10)))))=r e^(iθ) ⇒ r=(√(10)) and cosθ =((−1)/( (√(10)))) , sinθ =(3/( (√(10)))) ⇒tanθ =−3 ⇒θ =−arctan(3) ⇒ −1+3i =(√(10))e^(−i arctan(3)) =⇒(−1+3i)^(n−k) =10^((n−k)/2) e^(−(n−k)i arctan(3)) and (−1+3i)^(n−k) e^((−1+3i)x) = 10^((n−k)/2) (cos(n−k)arctan3)−isin(n−k)arctan(3)}e^(−x) {cos(3x)+isin(3x)} e^(−x) 10^((n−k)/2) {cos(3x)cos(n−k)arctan3 +isin(3x)cos(n−k)arctan3 −i cos(3x) sin(n−k)arctan3 +sin(3x)sin(n−k)arctan3 ⇒ f^((n)) (x)=Im(w^((n)) )= Σ_(k=0) ^n (−1)^k k! (C_n ^k /((x+1)^(k+1) )) e^(−x) 10^((n−k)/2) { sin(3x)cos{(n−k)arctan(3) −cos(3x) sin{(n−k)arctan(3)} ⇒ f^((n)) (0) =− Σ_(k=0) ^n (−1)^k k! C_n ^k 10^((n−k)/2) sin{(n−k)arctan3}
$$\left.\mathrm{1}\right)\:\:{we}\:{have}\:{f}\left({x}\right)={Im}\left(\frac{\mathrm{1}}{\mathrm{1}+{x}}{e}^{−{x}+\mathrm{3}{ix}} \right)\:=\:{Im}\left(\frac{\mathrm{1}}{\mathrm{1}+{x}}\:{e}^{\left(−\mathrm{1}+\mathrm{3}{i}\right){x}} \right)={Im}\left({w}\left({x}\right)\right)\:{we}\:{have} \\ $$$${w}\left({x}\right)^{\left({n}\right)} =\left\{\frac{\mathrm{1}}{\mathrm{1}+{x}}\:{e}^{\left(−\mathrm{1}+\mathrm{3}{i}\right){x}} \right\}^{\left({n}\right)} \:=_{{leibniz}} \:\:\:\:\:\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left(\frac{\mathrm{1}}{\mathrm{1}+{x}}\right)^{\left({k}\right)} \:\left({e}^{\left(−\mathrm{1}+\mathrm{3}{i}\right){x}} \right)^{\left({n}−{k}\right)} \\ $$$${but}\:\left({e}^{{zx}} \right)^{\left({k}\right)} \:=_{{zfixed}} \:\:\:\:{z}^{{k}} \:{e}^{{zx}} \:\Rightarrow\left\{{e}^{\left(−\mathrm{1}+\mathrm{3}{i}\right){x}} \right\}^{\left({n}−{k}\right)} =\left(−\mathrm{1}+\mathrm{3}{i}\right)^{{n}−{k}} \:{e}^{\left(−\mathrm{1}+\mathrm{3}{i}\right){x}} \:\:\:{also} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{1}+{x}}\right)^{\left({k}\right)} \:=\frac{\left(−\mathrm{1}\right)^{{k}} \:{k}!}{\left(\mathrm{1}+{x}\right)^{{k}+\mathrm{1}} }\:\Rightarrow{w}^{\left({n}\right)} \left({x}\right)\:=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:\frac{\left(−\mathrm{1}\right)^{{k}} \:{k}!}{\left(\mathrm{1}+{x}\right)^{{k}+\mathrm{1}} }\:\left(−\mathrm{1}+\mathrm{3}{i}\right)^{{n}−{k}} \:{e}^{\left(−\mathrm{1}+\mathrm{3}{i}\right){x}} \\ $$$$\:\:{we}\:{have}\:\mid−\mathrm{1}+\mathrm{3}{i}\mid\:=\sqrt{\mathrm{1}+\mathrm{9}}=\sqrt{\mathrm{10}}\:\Rightarrow−\mathrm{1}+\mathrm{3}{i}\:=\sqrt{\mathrm{10}}\left(\frac{−\mathrm{1}}{\:\sqrt{\mathrm{10}}}\:+\frac{\mathrm{3}{i}}{\:\sqrt{\mathrm{10}}}\right)={r}\:{e}^{{i}\theta} \:\Rightarrow \\ $$$${r}=\sqrt{\mathrm{10}}\:\:\:{and}\:\:\:{cos}\theta\:=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{10}}}\:,\:{sin}\theta\:=\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}\:\Rightarrow{tan}\theta\:=−\mathrm{3}\:\Rightarrow\theta\:=−{arctan}\left(\mathrm{3}\right)\:\Rightarrow \\ $$$$−\mathrm{1}+\mathrm{3}{i}\:=\sqrt{\mathrm{10}}{e}^{−{i}\:{arctan}\left(\mathrm{3}\right)} \:=\Rightarrow\left(−\mathrm{1}+\mathrm{3}{i}\right)^{{n}−{k}} \:=\mathrm{10}^{\frac{{n}−{k}}{\mathrm{2}}} \:\:{e}^{−\left({n}−{k}\right){i}\:{arctan}\left(\mathrm{3}\right)} \\ $$$${and}\:\:\left(−\mathrm{1}+\mathrm{3}{i}\right)^{{n}−{k}} \:{e}^{\left(−\mathrm{1}+\mathrm{3}{i}\right){x}} \:= \\ $$$$\left.\mathrm{10}^{\frac{{n}−{k}}{\mathrm{2}}} \:\left({cos}\left({n}−{k}\right){arctan}\mathrm{3}\right)−{isin}\left({n}−{k}\right){arctan}\left(\mathrm{3}\right)\right\}{e}^{−{x}} \left\{{cos}\left(\mathrm{3}{x}\right)+{isin}\left(\mathrm{3}{x}\right)\right\} \\ $$$${e}^{−{x}} \:\mathrm{10}^{\frac{{n}−{k}}{\mathrm{2}}} \left\{{cos}\left(\mathrm{3}{x}\right){cos}\left({n}−{k}\right){arctan}\mathrm{3}\:+{isin}\left(\mathrm{3}{x}\right){cos}\left({n}−{k}\right){arctan}\mathrm{3}\right. \\ $$$$−{i}\:{cos}\left(\mathrm{3}{x}\right)\:{sin}\left({n}−{k}\right){arctan}\mathrm{3}\:+{sin}\left(\mathrm{3}{x}\right){sin}\left({n}−{k}\right){arctan}\mathrm{3} \\ $$$$\Rightarrow\:{f}^{\left({n}\right)} \left({x}\right)={Im}\left({w}^{\left({n}\right)} \right)= \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\:\left(−\mathrm{1}\right)^{{k}} {k}!\:\:\frac{{C}_{{n}} ^{{k}} }{\left({x}+\mathrm{1}\right)^{{k}+\mathrm{1}} }\:{e}^{−{x}} \:\mathrm{10}^{\frac{{n}−{k}}{\mathrm{2}}} \left\{\:\:{sin}\left(\mathrm{3}{x}\right){cos}\left\{\left({n}−{k}\right){arctan}\left(\mathrm{3}\right)\right.\right. \\ $$$$−{cos}\left(\mathrm{3}{x}\right)\:{sin}\left\{\left({n}−{k}\right){arctan}\left(\mathrm{3}\right)\right\}\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left(\mathrm{0}\right)\:=−\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\left(−\mathrm{1}\right)^{{k}} {k}!\:\:\:{C}_{{n}} ^{{k}} \:\:\mathrm{10}^{\frac{{n}−{k}}{\mathrm{2}}} \:\:{sin}\left\{\left({n}−{k}\right){arctan}\mathrm{3}\right\} \\ $$
Commented by maxmathsup by imad last updated on 03/Jun/19
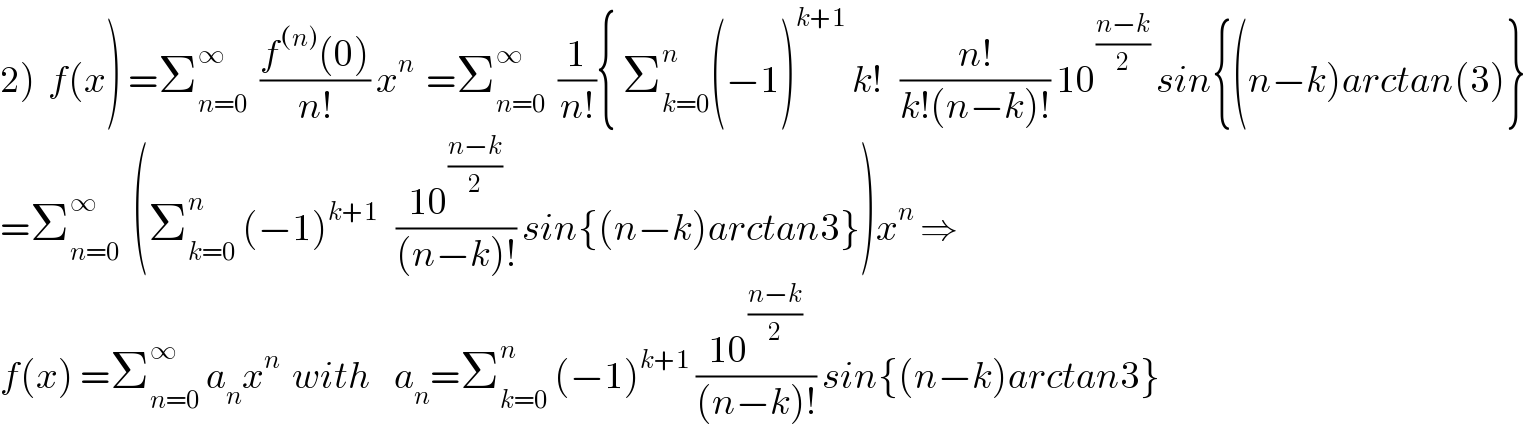
2) f(x) =Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n =Σ_(n=0) ^∞ (1/(n!)){ Σ_(k=0) ^n (−1)^(k+1) k! ((n!)/(k!(n−k)!)) 10^((n−k)/2) sin{(n−k)arctan(3)} =Σ_(n=0) ^∞ (Σ_(k=0) ^n (−1)^(k+1) ((10^((n−k)/2) )/((n−k)!)) sin{(n−k)arctan3})x^n ⇒ f(x) =Σ_(n=0) ^∞ a_n x^n with a_n =Σ_(k=0) ^n (−1)^(k+1) ((10^((n−k)/2) )/((n−k)!)) sin{(n−k)arctan3}
$$\left.\mathrm{2}\right)\:\:{f}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \:\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}!}\left\{\:\sum_{{k}=\mathrm{0}} ^{{n}} \left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \:{k}!\:\:\:\frac{{n}!}{{k}!\left({n}−{k}\right)!}\:\mathrm{10}^{\frac{{n}−{k}}{\mathrm{2}}} \:{sin}\left\{\left({n}−{k}\right){arctan}\left(\mathrm{3}\right)\right\}\right. \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \:\:\:\frac{\mathrm{10}^{\frac{{n}−{k}}{\mathrm{2}}} }{\left({n}−{k}\right)!}\:{sin}\left\{\left({n}−{k}\right){arctan}\mathrm{3}\right\}\right){x}^{{n}} \:\Rightarrow \\ $$$${f}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:{a}_{{n}} {x}^{{n}} \:\:{with}\:\:\:\:{a}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \:\frac{\mathrm{10}^{\frac{{n}−{k}}{\mathrm{2}}} }{\left({n}−{k}\right)!}\:{sin}\left\{\left({n}−{k}\right){arctan}\mathrm{3}\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *