Menu Close

let-f-x-e-x-2-ln-2-x-developp-f-at-integr-serie-

Tinku Tara 0 Comments
Pin




Question Number 60701 by maxmathsup by imad last updated on 24/May/19
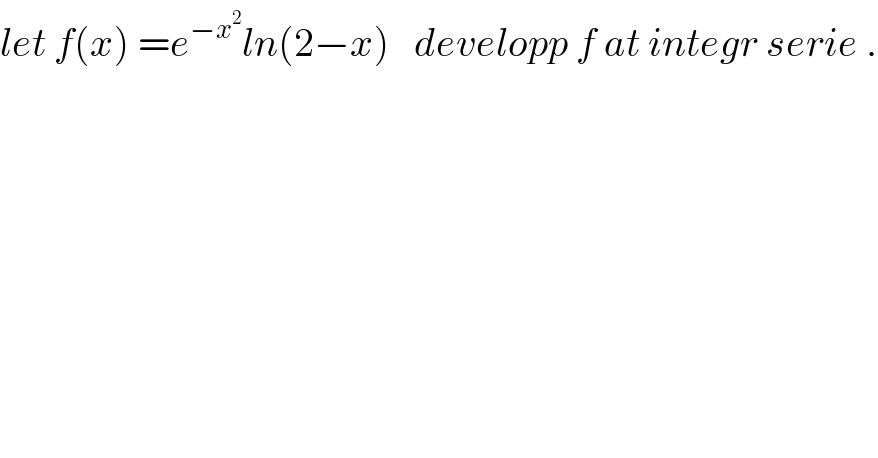
let f(x) =e^(−x^2 ) ln(2−x) developp f at integr serie .
$${let}\:{f}\left({x}\right)\:={e}^{−{x}^{\mathrm{2}} } {ln}\left(\mathrm{2}−{x}\right)\:\:\:{developp}\:{f}\:{at}\:{integr}\:{serie}\:. \\ $$
Commented by maxmathsup by imad last updated on 27/May/19
we have f(x) =e^(−x^2 ) ln(2(1−(x/2))) =ln(2) e^(−x^2 ) +e^(−x^2 ) ln(1−(x/2)) if ∣(x/2)∣<1 ⇒−2<x<2 we get e^(−x^2 ) =Σ_(n=0) ^∞ (((−x^2 )^n )/(n!)) =Σ_(n=0) ^∞ (((−1)^n x^(2n) )/(n!)) ln(1+u) =Σ_(n=1) ^∞ (−1)^(n−1) (u^n /n) ⇒ln(1−u) =−Σ_(n=1) ^∞ (u^n /n) ⇒ ln(1−(x/2)) =−Σ_(n=1) ^∞ (x^n /(n2^n )) ⇒f(x)=ln(2)Σ_(n=0) ^∞ (((−1)^n x^(2n) )/(n!)) −(Σ_(n=0) ^∞ (((−1)^n x^(2n) )/(n!)))(Σ_(n=1) ^∞ (x^n /(n2^n ))) =ln(2)Σ_(n=0) ^∞ (((−1)^n x^(2n) )/(n!)) −Σ_(n=1) ^∞ (x^n /(n2^n )) +(Σ_(n=1) ^∞ (((−1)^n )/(n!)) x^(2n) )(Σ_(n=1) ^∞ (1/(n2^n ))x^n ) let a_n =(((−1)^n )/(n!)) x^(2n) and b_n =(1/(n2^n ))x^n ⇒ (Σ_(n=1) ^∞ (...))(Σ(...)) =(Σ_(n=1) ^∞ a_n ) (Σ_(n=1) ^∞ b_n ) =Σ_(n=1) ^∞ c_n c_n =Σ_(i+j=n ) a_i b_j =Σ_(i=1) ^n a_i b_(n−i) =Σ_(i=1) ^n (((−1)^i )/(i!)) x^(2i) (1/((n−i)2^(n−i) )) x^(n−i) =Σ_(i=1) ^n (((−1)^i )/(i!(n−i)2^(n−i) )) x^(n+i) ⇒ f(x) =ln(2)Σ_(n=0) ^∞ (((−1)^n x^(2n) )/(n!)) −Σ_(n=1) ^∞ (x^n /(n 2^n )) +Σ_(n=1) ^∞ (Σ_(i=1) ^n (((−1)^i )/(i!(n−i)!2^(n−i) ))x^i )x^n ....be continued....
$${we}\:{have}\:{f}\left({x}\right)\:={e}^{−{x}^{\mathrm{2}} } {ln}\left(\mathrm{2}\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)\right)\:={ln}\left(\mathrm{2}\right)\:{e}^{−{x}^{\mathrm{2}} } \:+{e}^{−{x}^{\mathrm{2}} } {ln}\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right) \\ $$$${if}\:\mid\frac{{x}}{\mathrm{2}}\mid<\mathrm{1}\:\Rightarrow−\mathrm{2}<{x}<\mathrm{2}\:\:{we}\:{get}\:\:{e}^{−{x}^{\mathrm{2}} } \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−{x}^{\mathrm{2}} \right)^{{n}} }{{n}!}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{{n}!} \\ $$$${ln}\left(\mathrm{1}+{u}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:\frac{{u}^{{n}} }{{n}}\:\Rightarrow{ln}\left(\mathrm{1}−{u}\right)\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \frac{{u}^{{n}} }{{n}}\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}\mathrm{2}^{{n}} }\:\:\Rightarrow{f}\left({x}\right)={ln}\left(\mathrm{2}\right)\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}} }{{n}!} \\ $$$$−\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}} }{{n}!}\right)\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{x}^{{n}} }{{n}\mathrm{2}^{{n}} }\right)\: \\ $$$$={ln}\left(\mathrm{2}\right)\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{{n}!}\:−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}\mathrm{2}^{{n}} }\:+\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\:{x}^{\mathrm{2}{n}} \right)\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}\mathrm{2}^{{n}} }{x}^{{n}} \right) \\ $$$${let}\:{a}_{{n}} =\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\:{x}^{\mathrm{2}{n}} \:\:\:{and}\:{b}_{{n}} =\frac{\mathrm{1}}{{n}\mathrm{2}^{{n}} }{x}^{{n}} \:\Rightarrow \\ $$$$\left(\sum_{{n}=\mathrm{1}} ^{\infty} \left(…\right)\right)\left(\Sigma\left(…\right)\right)\:=\left(\sum_{{n}=\mathrm{1}} ^{\infty} {a}_{{n}} \right)\:\left(\sum_{{n}=\mathrm{1}} ^{\infty} {b}_{{n}} \right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{c}_{{n}} \\ $$$${c}_{{n}} =\sum_{{i}+{j}={n}\:} \:\:{a}_{{i}} {b}_{{j}} \:\:=\sum_{{i}=\mathrm{1}} ^{{n}} \:{a}_{{i}} \:{b}_{{n}−{i}} \:\:\:=\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{i}} }{{i}!}\:{x}^{\mathrm{2}{i}} \:\:\:\:\frac{\mathrm{1}}{\left({n}−{i}\right)\mathrm{2}^{{n}−{i}} }\:{x}^{{n}−{i}} \\ $$$$=\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{i}} }{{i}!\left({n}−{i}\right)\mathrm{2}^{{n}−{i}} }\:{x}^{{n}+{i}} \:\Rightarrow \\ $$$${f}\left({x}\right)\:={ln}\left(\mathrm{2}\right)\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{{n}!}\:−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}\:\mathrm{2}^{{n}} }\:+\sum_{{n}=\mathrm{1}} ^{\infty} \left(\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{i}} }{{i}!\left({n}−{i}\right)!\mathrm{2}^{{n}−{i}} }{x}^{{i}} \right){x}^{{n}} \\ $$$$….{be}\:{continued}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *