Question Number 98309 by Rio Michael last updated on 12/Jun/20
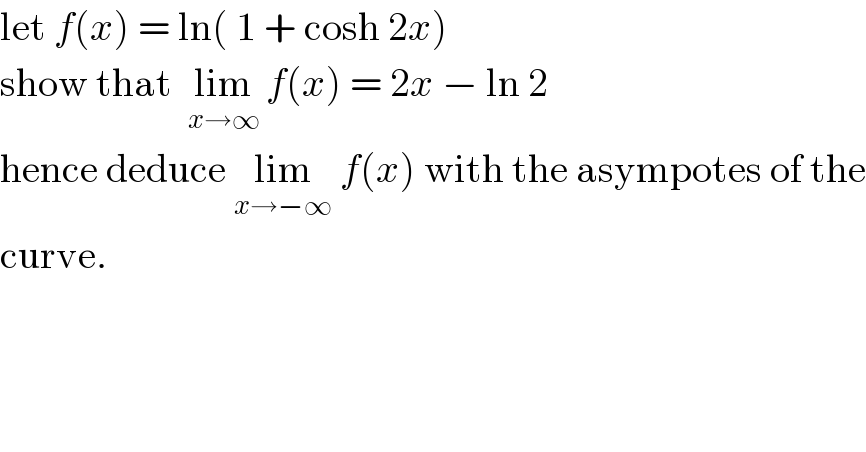
$$\mathrm{let}\:{f}\left({x}\right)\:=\:\mathrm{ln}\left(\:\mathrm{1}\:+\:\mathrm{cosh}\:\mathrm{2}{x}\right) \\ $$$$\mathrm{show}\:\mathrm{that}\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{f}\left({x}\right)\:=\:\mathrm{2}{x}\:−\:\mathrm{ln}\:\mathrm{2} \\ $$$$\mathrm{hence}\:\mathrm{deduce}\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{f}\left({x}\right)\:\mathrm{with}\:\mathrm{the}\:\mathrm{asympotes}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{curve}. \\ $$
Answered by abdomathmax last updated on 13/Jun/20
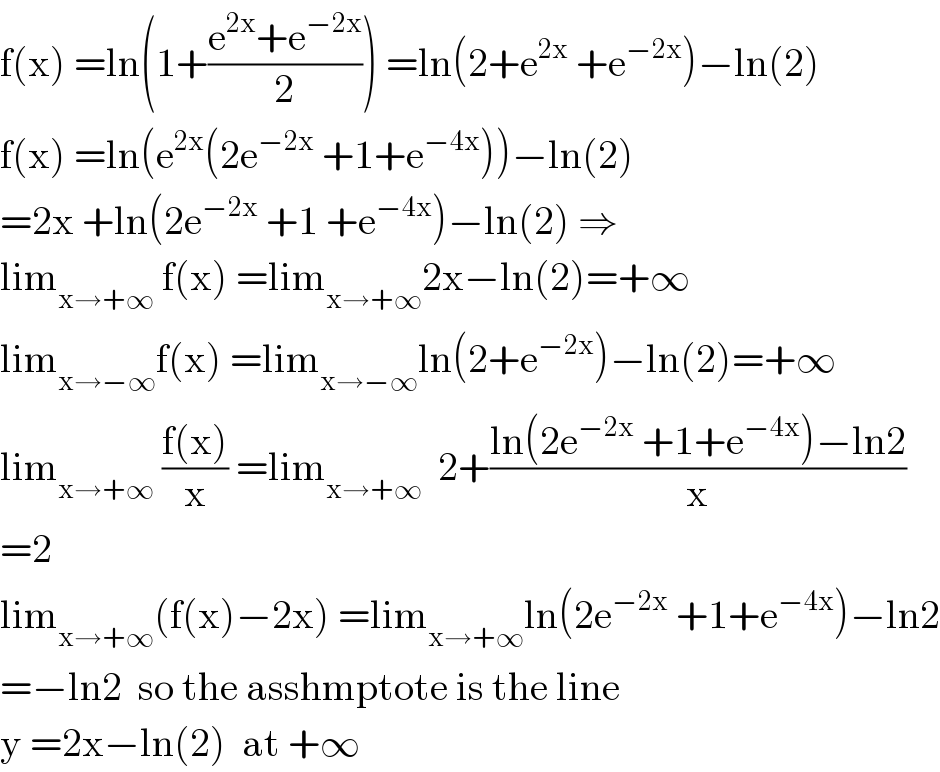
$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{e}^{\mathrm{2x}} +\mathrm{e}^{−\mathrm{2x}} }{\mathrm{2}}\right)\:=\mathrm{ln}\left(\mathrm{2}+\mathrm{e}^{\mathrm{2x}} \:+\mathrm{e}^{−\mathrm{2x}} \right)−\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{ln}\left(\mathrm{e}^{\mathrm{2x}} \left(\mathrm{2e}^{−\mathrm{2x}} \:+\mathrm{1}+\mathrm{e}^{−\mathrm{4x}} \right)\right)−\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$=\mathrm{2x}\:+\mathrm{ln}\left(\mathrm{2e}^{−\mathrm{2x}} \:+\mathrm{1}\:+\mathrm{e}^{−\mathrm{4x}} \right)−\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{2x}−\mathrm{ln}\left(\mathrm{2}\right)=+\infty \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \mathrm{ln}\left(\mathrm{2}+\mathrm{e}^{−\mathrm{2x}} \right)−\mathrm{ln}\left(\mathrm{2}\right)=+\infty \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{x}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\:\mathrm{2}+\frac{\mathrm{ln}\left(\mathrm{2e}^{−\mathrm{2x}} \:+\mathrm{1}+\mathrm{e}^{−\mathrm{4x}} \right)−\mathrm{ln2}}{\mathrm{x}} \\ $$$$=\mathrm{2} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \left(\mathrm{f}\left(\mathrm{x}\right)−\mathrm{2x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{ln}\left(\mathrm{2e}^{−\mathrm{2x}} \:+\mathrm{1}+\mathrm{e}^{−\mathrm{4x}} \right)−\mathrm{ln2} \\ $$$$=−\mathrm{ln2}\:\:\mathrm{so}\:\mathrm{the}\:\mathrm{asshmptote}\:\mathrm{is}\:\mathrm{the}\:\mathrm{line} \\ $$$$\mathrm{y}\:=\mathrm{2x}−\mathrm{ln}\left(\mathrm{2}\right)\:\:\mathrm{at}\:+\infty \\ $$
Commented by mathmax by abdo last updated on 13/Jun/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}. \\ $$
Commented by Rio Michael last updated on 13/Jun/20
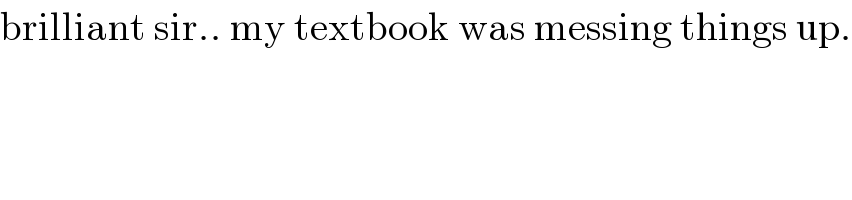
$$\mathrm{brilliant}\:\mathrm{sir}..\:\mathrm{my}\:\mathrm{textbook}\:\mathrm{was}\:\mathrm{messing}\:\mathrm{things}\:\mathrm{up}. \\ $$
