Question Number 34697 by abdo imad last updated on 10/May/18
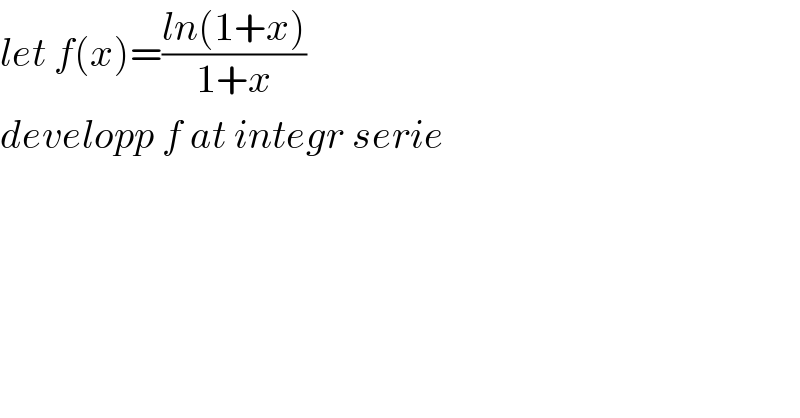
$${let}\:{f}\left({x}\right)=\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}} \\ $$$${developp}\:{f}\:{at}\:{integr}\:{serie} \\ $$
Commented by math khazana by abdo last updated on 11/May/18
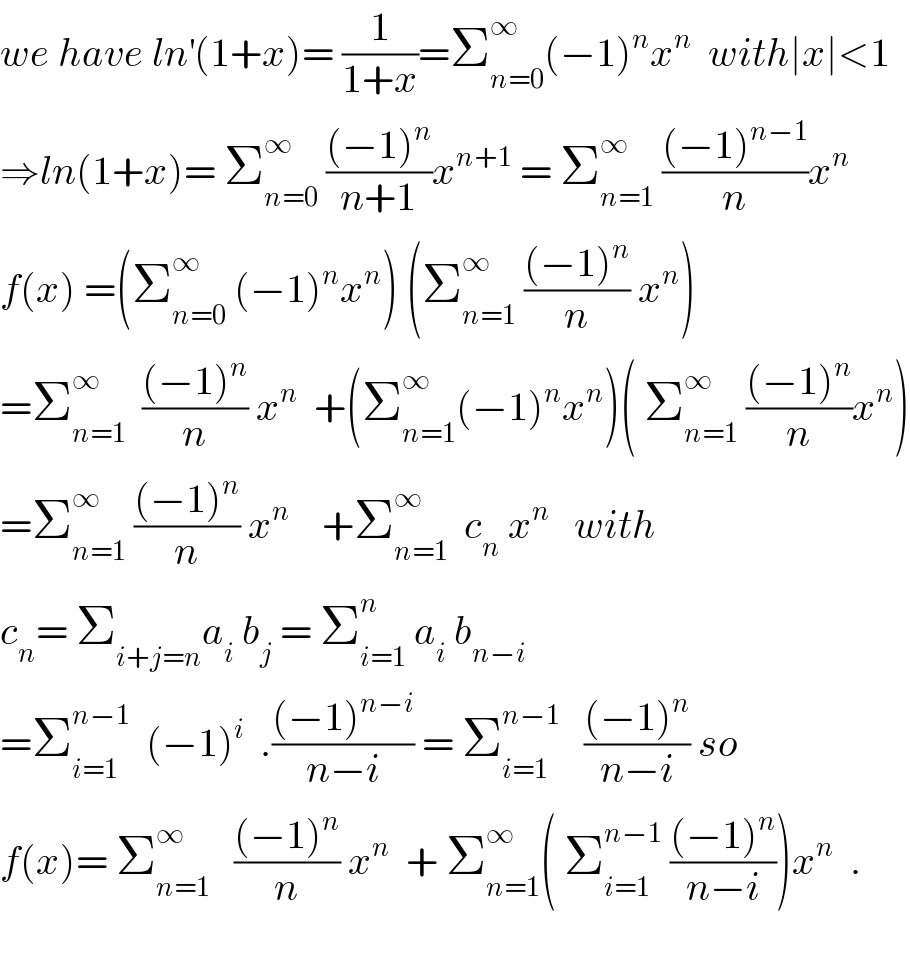
$${we}\:{have}\:{ln}^{'} \left(\mathrm{1}+{x}\right)=\:\frac{\mathrm{1}}{\mathrm{1}+{x}}=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \:\:{with}\mid{x}\mid<\mathrm{1} \\ $$$$\Rightarrow{ln}\left(\mathrm{1}+{x}\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} \:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{x}^{{n}} \\ $$$${f}\left({x}\right)\:=\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \right)\:\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:{x}^{{n}} \right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:{x}^{{n}} \:\:+\left(\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \right)\left(\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}{x}^{{n}} \right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:{x}^{{n}} \:\:\:\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:{c}_{{n}} \:{x}^{{n}} \:\:\:{with} \\ $$$${c}_{{n}} =\:\sum_{{i}+{j}={n}} {a}_{{i}} \:{b}_{{j}} \:=\:\sum_{{i}=\mathrm{1}} ^{{n}} \:{a}_{{i}} \:{b}_{{n}−{i}} \\ $$$$=\sum_{{i}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\:\left(−\mathrm{1}\right)^{{i}} \:\:.\frac{\left(−\mathrm{1}\right)^{{n}−{i}} }{{n}−{i}}\:=\:\sum_{{i}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}−{i}}\:{so} \\ $$$${f}\left({x}\right)=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:{x}^{{n}} \:\:+\:\sum_{{n}=\mathrm{1}} ^{\infty} \left(\:\sum_{{i}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}−{i}}\right){x}^{{n}} \:\:. \\ $$$$ \\ $$
