Question Number 96194 by mathmax by abdo last updated on 30/May/20

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{ln}\left(\mathrm{cosx}\right)\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$
Answered by john santu last updated on 30/May/20
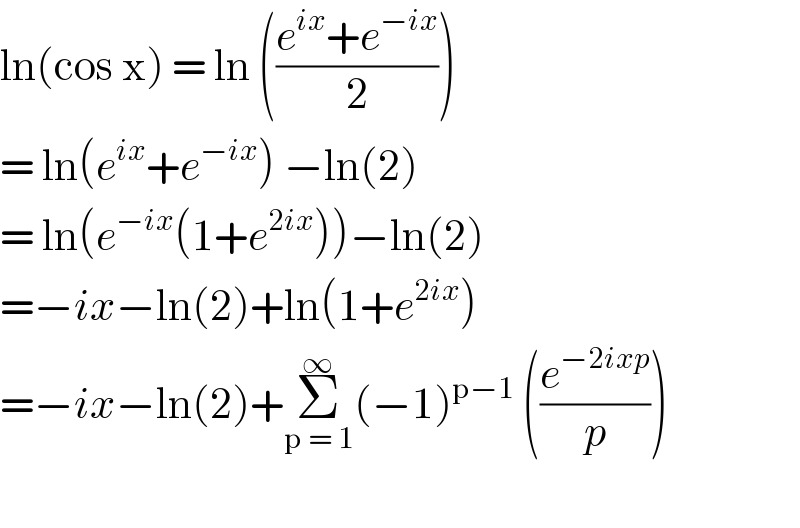
$$\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\:=\:\mathrm{ln}\:\left(\frac{{e}^{{ix}} +{e}^{−{ix}} }{\mathrm{2}}\right) \\ $$$$=\:\mathrm{ln}\left({e}^{{ix}} +{e}^{−{ix}} \right)\:−\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$=\:\mathrm{ln}\left({e}^{−{ix}} \left(\mathrm{1}+{e}^{\mathrm{2}{ix}} \right)\right)−\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$=−{ix}−\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{ln}\left(\mathrm{1}+{e}^{\mathrm{2}{ix}} \right)\: \\ $$$$=−{ix}−\mathrm{ln}\left(\mathrm{2}\right)+\underset{\mathrm{p}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{p}−\mathrm{1}} \:\left(\frac{{e}^{−\mathrm{2}{ixp}} }{{p}}\right) \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 30/May/20
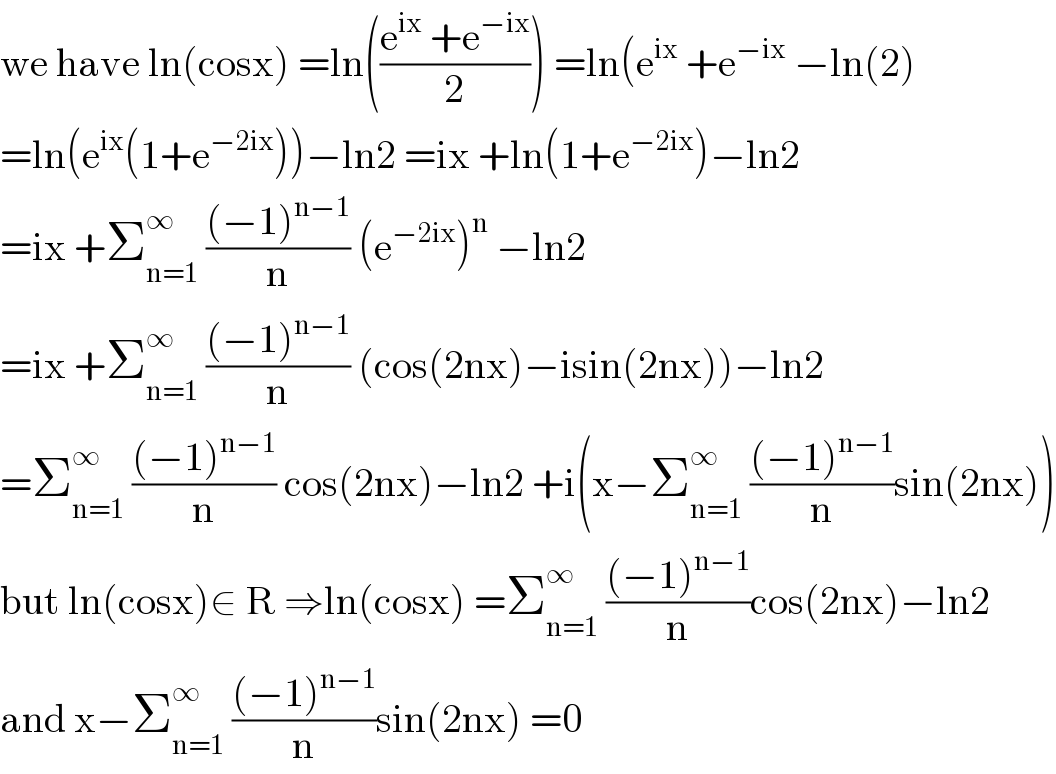
$$\mathrm{we}\:\mathrm{have}\:\mathrm{ln}\left(\mathrm{cosx}\right)\:=\mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{ix}} \:+\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2}}\right)\:=\mathrm{ln}\left(\mathrm{e}^{\mathrm{ix}} \:+\mathrm{e}^{−\mathrm{ix}} \:−\mathrm{ln}\left(\mathrm{2}\right)\right. \\ $$$$=\mathrm{ln}\left(\mathrm{e}^{\mathrm{ix}} \left(\mathrm{1}+\mathrm{e}^{−\mathrm{2ix}} \right)\right)−\mathrm{ln2}\:=\mathrm{ix}\:+\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2ix}} \right)−\mathrm{ln2} \\ $$$$=\mathrm{ix}\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\left(\mathrm{e}^{−\mathrm{2ix}} \right)^{\mathrm{n}} \:−\mathrm{ln2} \\ $$$$=\mathrm{ix}\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\left(\mathrm{cos}\left(\mathrm{2nx}\right)−\mathrm{isin}\left(\mathrm{2nx}\right)\right)−\mathrm{ln2} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\mathrm{cos}\left(\mathrm{2nx}\right)−\mathrm{ln2}\:+\mathrm{i}\left(\mathrm{x}−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\mathrm{sin}\left(\mathrm{2nx}\right)\right) \\ $$$$\mathrm{but}\:\mathrm{ln}\left(\mathrm{cosx}\right)\in\:\mathrm{R}\:\Rightarrow\mathrm{ln}\left(\mathrm{cosx}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\mathrm{cos}\left(\mathrm{2nx}\right)−\mathrm{ln2} \\ $$$$\mathrm{and}\:\mathrm{x}−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\mathrm{sin}\left(\mathrm{2nx}\right)\:=\mathrm{0} \\ $$
