Menu Close

let-f-x-ln-x-1-x-1-1-determine-D-f-2-calculatef-n-x-and-f-n-0-3-developp-f-at-integr-serie-4-calculate-1-2-1-2-f-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 62882 by mathmax by abdo last updated on 26/Jun/19
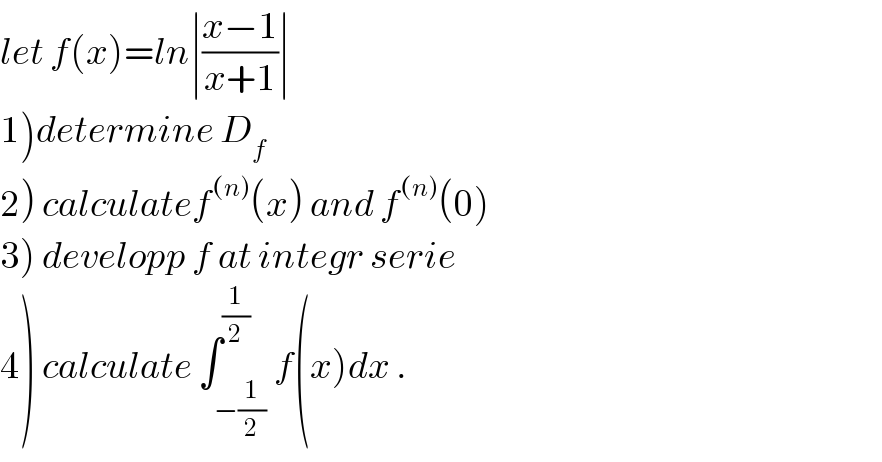
let f(x)=ln∣((x−1)/(x+1))∣ 1)determine D_f 2) calculatef^((n)) (x) and f^((n)) (0) 3) developp f at integr serie 4) calculate ∫_(−(1/2)) ^(1/2) f(x)dx .
$${let}\:{f}\left({x}\right)={ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid \\ $$$$\left.\mathrm{1}\right){determine}\:{D}_{{f}} \\ $$$$\left.\mathrm{2}\right)\:{calculatef}^{\left({n}\right)} \left({x}\right)\:{and}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{3}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie} \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {f}\left({x}\right){dx}\:. \\ $$
Commented by mathmax by abdo last updated on 27/Jun/19
4) ∫_(−(1/2)) ^(1/2) ln∣((x−1)/(x+1))∣dx =∫_(−(1/2)) ^(1/2) ln∣1−x∣ dx −∫_(−(1/2)) ^(1/2) ln∣1+x∣ dx =∫_(−(1/2)) ^(1/2) ln(1−x)dx −∫_(−(1/2)) ^(1/2) ln(1+x)dx =H−K H =_(1−x =t) ∫_(3/2) ^(1/2) ln(t)(−dt) =∫_(1/2) ^(3/2) ln(t)dt =[tln(t)−t]_(1/2) ^(3/2) =(3/2)ln((3/2))−(3/2) −(1/2)ln((1/2))+(1/2) K =∫_(−(1/2)) ^(1/2) ln(1+x)dx =_(1+x =t) ∫_(1/2) ^(3/2) ln(t)dt =[tln(t)−t]_(1/2) ^(3/2) =(3/2)ln((3/2))−(3/2) −(1/2)ln((1/2))+(1/2) ⇒ A =(3/2)ln((3/2))−(3/2) −(1/2)ln((1/2))+(1/2) −(3/2)ln((3/2))+(3/2) +(1/2)ln((1/2))−(1/2) ⇒ A =0 another[way let prove that f is odd we have f(−x) =ln∣((−x−1)/(−x+1))∣ =ln∣((x+1)/(x−1))∣ =−ln∣((x−1)/(x+1))∣=−f(x) ⇒ ∫_(−(1/2)) ^(1/2) f(x)dx =0.
$$\left.\mathrm{4}\right)\:\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid{dx}\:=\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {ln}\mid\mathrm{1}−{x}\mid\:{dx}\:−\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:{ln}\mid\mathrm{1}+{x}\mid\:{dx} \\ $$$$=\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {ln}\left(\mathrm{1}−{x}\right){dx}\:−\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:{ln}\left(\mathrm{1}+{x}\right){dx}\:={H}−{K} \\ $$$${H}\:=_{\mathrm{1}−{x}\:={t}} \:\:\:\:\:\int_{\frac{\mathrm{3}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {ln}\left({t}\right)\left(−{dt}\right)\:=\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{3}}{\mathrm{2}}} {ln}\left({t}\right){dt}\:=\left[{tln}\left({t}\right)−{t}\right]_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\frac{\mathrm{3}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${K}\:=\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {ln}\left(\mathrm{1}+{x}\right){dx}\:=_{\mathrm{1}+{x}\:={t}} \:\:\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{3}}{\mathrm{2}}} \:{ln}\left({t}\right){dt}\:=\left[{tln}\left({t}\right)−{t}\right]_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\frac{\mathrm{3}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${A}\:=\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\frac{\mathrm{3}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\frac{\mathrm{3}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${A}\:=\mathrm{0}\:\:\: \\ $$$${another}\left[{way}\:\:{let}\:{prove}\:{that}\:{f}\:{is}\:{odd}\:{we}\:{have}\right. \\ $$$${f}\left(−{x}\right)\:={ln}\mid\frac{−{x}−\mathrm{1}}{−{x}+\mathrm{1}}\mid\:={ln}\mid\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\mid\:=−{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid=−{f}\left({x}\right)\:\Rightarrow\:\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {f}\left({x}\right){dx}\:=\mathrm{0}. \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 27/Jun/19
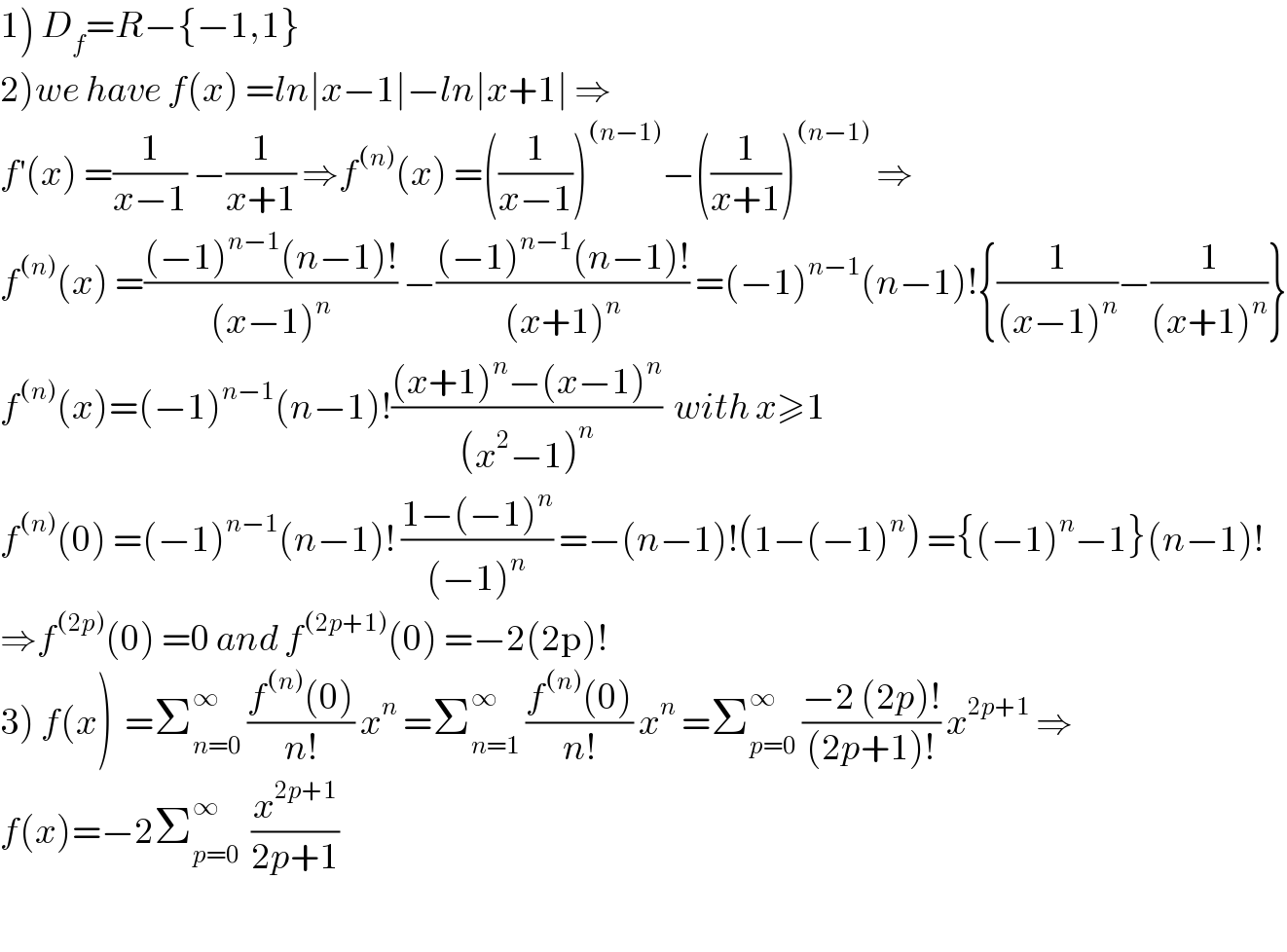
1) D_f =R−{−1,1} 2)we have f(x) =ln∣x−1∣−ln∣x+1∣ ⇒ f^′ (x) =(1/(x−1)) −(1/(x+1)) ⇒f^((n)) (x) =((1/(x−1)))^((n−1)) −((1/(x+1)))^((n−1)) ⇒ f^((n)) (x) =(((−1)^(n−1) (n−1)!)/((x−1)^n )) −(((−1)^(n−1) (n−1)!)/((x+1)^n )) =(−1)^(n−1) (n−1)!{(1/((x−1)^n ))−(1/((x+1)^n ))} f^((n)) (x)=(−1)^(n−1) (n−1)!(((x+1)^n −(x−1)^n )/((x^2 −1)^n )) with x≥1 f^((n)) (0) =(−1)^(n−1) (n−1)! ((1−(−1)^n )/((−1)^n )) =−(n−1)!(1−(−1)^n ) ={(−1)^n −1}(n−1)! ⇒f^((2p)) (0) =0 and f^((2p+1)) (0) =−2(2p)! 3) f(x) =Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n =Σ_(n=1) ^∞ ((f^((n)) (0))/(n!)) x^n =Σ_(p=0) ^∞ ((−2 (2p)!)/((2p+1)!)) x^(2p+1) ⇒ f(x)=−2Σ_(p=0) ^∞ (x^(2p+1) /(2p+1))
$$\left.\mathrm{1}\right)\:{D}_{{f}} ={R}−\left\{−\mathrm{1},\mathrm{1}\right\} \\ $$$$\left.\mathrm{2}\right){we}\:{have}\:{f}\left({x}\right)\:={ln}\mid{x}−\mathrm{1}\mid−{ln}\mid{x}+\mathrm{1}\mid\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\frac{\mathrm{1}}{{x}−\mathrm{1}}\:−\frac{\mathrm{1}}{{x}+\mathrm{1}}\:\Rightarrow{f}^{\left({n}\right)} \left({x}\right)\:=\left(\frac{\mathrm{1}}{{x}−\mathrm{1}}\right)^{\left({n}−\mathrm{1}\right)} −\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)^{\left({n}−\mathrm{1}\right)} \:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}−\mathrm{1}\right)^{{n}} }\:−\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}+\mathrm{1}\right)^{{n}} }\:=\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\left\{\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{{n}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{{n}} }\right\} \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\frac{\left({x}+\mathrm{1}\right)^{{n}} −\left({x}−\mathrm{1}\right)^{{n}} }{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{{n}} }\:\:{with}\:{x}\geqslant\mathrm{1} \\ $$$${f}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\:\frac{\mathrm{1}−\left(−\mathrm{1}\right)^{{n}} }{\left(−\mathrm{1}\right)^{{n}} }\:=−\left({n}−\mathrm{1}\right)!\left(\mathrm{1}−\left(−\mathrm{1}\right)^{{n}} \right)\:=\left\{\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}\right\}\left({n}−\mathrm{1}\right)! \\ $$$$\Rightarrow{f}^{\left(\mathrm{2}{p}\right)} \left(\mathrm{0}\right)\:=\mathrm{0}\:{and}\:{f}^{\left(\mathrm{2}{p}+\mathrm{1}\right)} \left(\mathrm{0}\right)\:=−\mathrm{2}\left(\mathrm{2p}\right)! \\ $$$$\left.\mathrm{3}\right)\:{f}\left({x}\right)\:\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \:=\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{−\mathrm{2}\:\left(\mathrm{2}{p}\right)!}{\left(\mathrm{2}{p}+\mathrm{1}\right)!}\:{x}^{\mathrm{2}{p}+\mathrm{1}} \:\Rightarrow\: \\ $$$${f}\left({x}\right)=−\mathrm{2}\sum_{{p}=\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{2}{p}+\mathrm{1}} }{\mathrm{2}{p}+\mathrm{1}} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 27/Jun/19
sorry i have flaged the post by error...
$${sorry}\:{i}\:{have}\:{flaged}\:{the}\:{post}\:{by}\:{error}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *