Menu Close

let-f-x-x-1-x-2-and-3-4-solve-in-R-f-f-f-x-0-

Tinku Tara 0 Comments
Pin




Question Number 151747 by mathdanisur last updated on 22/Aug/21
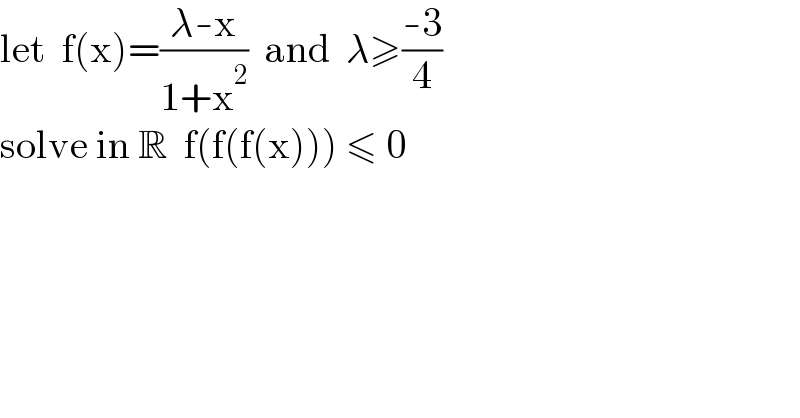
let f(x)=((λ-x)/(1+x^2 )) and λ≥((-3)/4) solve in R f(f(f(x))) ≤ 0
$$\mathrm{let}\:\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\lambda-\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\:\mathrm{and}\:\:\lambda\geqslant\frac{-\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{solve}\:\mathrm{in}\:\mathbb{R}\:\:\mathrm{f}\left(\mathrm{f}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\right)\:\leqslant\:\mathrm{0} \\ $$
Answered by mr W last updated on 22/Aug/21
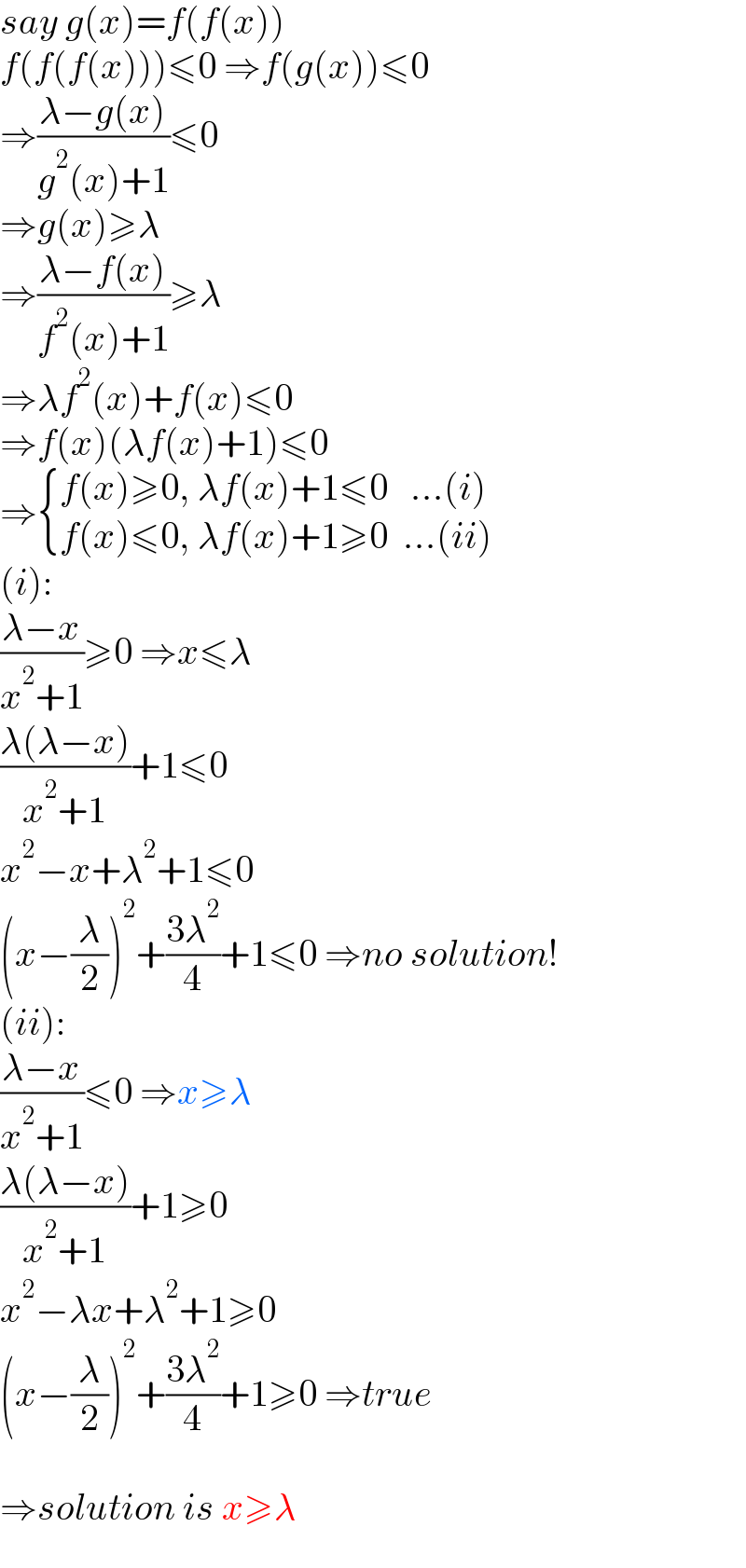
say g(x)=f(f(x)) f(f(f(x)))≤0 ⇒f(g(x))≤0 ⇒((λ−g(x))/(g^2 (x)+1))≤0 ⇒g(x)≥λ ⇒((λ−f(x))/(f^2 (x)+1))≥λ ⇒λf^2 (x)+f(x)≤0 ⇒f(x)(λf(x)+1)≤0 ⇒ { ((f(x)≥0, λf(x)+1≤0 ...(i))),((f(x)≤0, λf(x)+1≥0 ...(ii))) :} (i): ((λ−x)/(x^2 +1))≥0 ⇒x≤λ ((λ(λ−x))/(x^2 +1))+1≤0 x^2 −x+λ^2 +1≤0 (x−(λ/2))^2 +((3λ^2 )/4)+1≤0 ⇒no solution! (ii): ((λ−x)/(x^2 +1))≤0 ⇒x≥λ ((λ(λ−x))/(x^2 +1))+1≥0 x^2 −λx+λ^2 +1≥0 (x−(λ/2))^2 +((3λ^2 )/4)+1≥0 ⇒true ⇒solution is x≥λ
$${say}\:{g}\left({x}\right)={f}\left({f}\left({x}\right)\right) \\ $$$${f}\left({f}\left({f}\left({x}\right)\right)\right)\leqslant\mathrm{0}\:\Rightarrow{f}\left({g}\left({x}\right)\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\frac{\lambda−{g}\left({x}\right)}{{g}^{\mathrm{2}} \left({x}\right)+\mathrm{1}}\leqslant\mathrm{0} \\ $$$$\Rightarrow{g}\left({x}\right)\geqslant\lambda \\ $$$$\Rightarrow\frac{\lambda−{f}\left({x}\right)}{{f}^{\mathrm{2}} \left({x}\right)+\mathrm{1}}\geqslant\lambda \\ $$$$\Rightarrow\lambda{f}^{\mathrm{2}} \left({x}\right)+{f}\left({x}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}\right)\left(\lambda{f}\left({x}\right)+\mathrm{1}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{{f}\left({x}\right)\geqslant\mathrm{0},\:\lambda{f}\left({x}\right)+\mathrm{1}\leqslant\mathrm{0}\:\:\:…\left({i}\right)}\\{{f}\left({x}\right)\leqslant\mathrm{0},\:\lambda{f}\left({x}\right)+\mathrm{1}\geqslant\mathrm{0}\:\:…\left({ii}\right)}\end{cases} \\ $$$$\left({i}\right): \\ $$$$\frac{\lambda−{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\geqslant\mathrm{0}\:\Rightarrow{x}\leqslant\lambda \\ $$$$\frac{\lambda\left(\lambda−{x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}+\mathrm{1}\leqslant\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{x}+\lambda^{\mathrm{2}} +\mathrm{1}\leqslant\mathrm{0} \\ $$$$\left({x}−\frac{\lambda}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}\lambda^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}\leqslant\mathrm{0}\:\Rightarrow{no}\:{solution}! \\ $$$$\left({ii}\right): \\ $$$$\frac{\lambda−{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\leqslant\mathrm{0}\:\Rightarrow{x}\geqslant\lambda \\ $$$$\frac{\lambda\left(\lambda−{x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}+\mathrm{1}\geqslant\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\lambda{x}+\lambda^{\mathrm{2}} +\mathrm{1}\geqslant\mathrm{0} \\ $$$$\left({x}−\frac{\lambda}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}\lambda^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}\geqslant\mathrm{0}\:\Rightarrow{true} \\ $$$$ \\ $$$$\Rightarrow{solution}\:{is}\:{x}\geqslant\lambda \\ $$
Commented by mr W last updated on 22/Aug/21
condition λ≥−(3/4) is not neccessary. the question is true for any λ∈R.
$${condition}\:\lambda\geqslant−\frac{\mathrm{3}}{\mathrm{4}}\:{is}\:{not}\:{neccessary}. \\ $$$${the}\:{question}\:{is}\:{true}\:{for}\:{any}\:\lambda\in\mathbb{R}. \\ $$
Commented by mathdanisur last updated on 23/Aug/21
Thank you Ser
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *