Question Number 37820 by prof Abdo imad last updated on 17/Jun/18
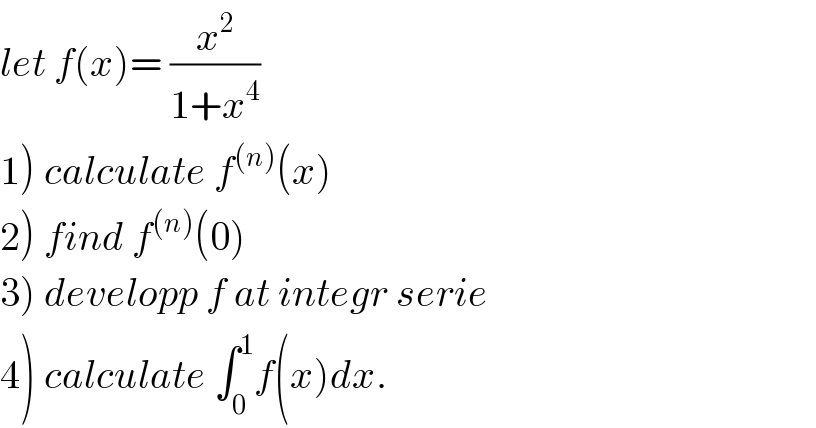
Commented by prof Abdo imad last updated on 18/Jun/18
Commented by prof Abdo imad last updated on 18/Jun/18
Answered by behi83417@gmail.com last updated on 18/Jun/18
![f(x)=(1/2).((2x^2 )/((x^2 +i)(x^2 −i)))=(1/2).(((x^2 +i)+(x^2 −i))/((x^2 +i)(x^2 −i)))= =(1/2)[(1/(x^2 +i))+(1/(x^2 −i))]=(1/2)[(1/((x+i(√i))(x−i(√i))))+ +(1/((x−(√i))(x+(√i))))]=(1/2)[(1/(2i(√i)))[(((x+i(√i))−(x−i(√i)))/((x+i(√i))(x−i(√i))))]+ +[(1/(2(√i)))[(((x+(√i))−(x−(√i)))/((x+(√i))(x−(√i))))]]=^((√i)=a) =−(a/4)[(1/(x−a^3 ))−(1/(x+a^3 ))+(i/(x−a))−(i/(x+a))] f^1 (x)=−(a/4)[((−1)/((x−a^3 )^2 ))+(1/((x+a^3 )^2 ))−(i/((x+a)^2 ))+(i/((x−a)^2 ))] f^n (x)=((n!a(−1)^n )/4)[(1/((x−a^3 )^(n+1) ))−(1/((x−a^3 )^(n+1) ))+ +(i/((x−a)^(n+1) ))−(i/((x−a)^(n+1) ))] . 2)f^n (0)=0 4)∫((x^2 dx)/(1+x^4 ))=−(a/4)[ln((x+a^3 )/(x−a^3 ))+i.ln((x+a)/(x−a))] F(1)=−(a/4)[ln((1+a^3 )/(1−a^3 ))+i.ln((1+a)/(1−a))]= −((√i)/4)[i(√i)+(√i)−i+i(i(√i)+(√i)+i)]= =−((√i)/4)[i(√i)+(√i)−i−(√i)+i(√i)−1]= =−((√i)/4)[2i(√i)−i−1]=−(1/4)(−2−i(√i)−(√i)) F(0)=−(a/4)[ln(−1)+i.ln(−1)]= =−(a/4)(((iπ)/2)+i.((iπ)/2))=−((π(√i))/8)(i−1)=((π(√i))/8)(1−i). I=F(1)−F(0)=(1/8)[4+(i+1)(√i)+π(√i)(i−1)]. i=cos(π/2)+isin(π/2)=e^((iπ)/2) ⇒(√i)=e^((iπ)/4) ((1+a^3 )/(1−a^3 ))=(((1+a^3 )^2 )/(1−a^6 ))=(((1+2i(√i)−i))/(1+i)).((1−i)/(1−i))= =(1/2)(1−i+2i(√i)+2(√i)−i−1)=i(√i)+(√i)−i ((1+a)/(1−a))=(((1+a)^2 )/(1−a^2 ))=((1+2(√i)+i)/(1−i)).((1+i)/(1+i))= =(1/2)(1+i+2(√i)+2i(√i)+i−1)=i(√i)+(√i)+i](https://www.tinkutara.com/question/Q37836.png)
Commented by math khazana by abdo last updated on 18/Jun/18
Commented by behi83417@gmail.com last updated on 18/Jun/18

