Menu Close

let-f-x-x-2-3-2x-1-1-calculate-0-1-f-x-dx-2-determine-f-1-x-and-calculate-f-1-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 56831 by maxmathsup by imad last updated on 24/Mar/19
let f(x) =(√(x^2 +3))−2x −1 1) calculate ∫_0 ^1 f(x)dx 2)determine f^(−1) (x) and calculate ∫ f^(−1) (x)dx .
$${let}\:{f}\left({x}\right)\:=\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}−\mathrm{2}{x}\:−\mathrm{1} \\ $$$$\left.\mathrm{1}\right)\:\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx} \\ $$$$\left.\mathrm{2}\right){determine}\:{f}^{−\mathrm{1}} \left({x}\right)\:{and}\:{calculate}\:\int\:{f}^{−\mathrm{1}} \left({x}\right){dx}\:. \\ $$
Commented by kaivan.ahmadi last updated on 25/Mar/19
I=∫_0 ^1 (√(x^2 +3))dx x=(√3)tgα⇒dx=(√3)sec^2 αdα (√(x^2 +3))=(√3)secα { ((x=0⇒α=0)),((x=1⇒α=(π/6))) :}⇒ I=3∫_0 ^(π/6) sec^3 αdα= (1/2)secαtgα+(1/2)ln∣secα+tgα∣]_0 ^(π/6) = ((1/2)×((√3)/2)×((√3)/3)+(1/2)ln(((√3)/2)+((√3)/3)))−0= (1/4)+(1/2)ln(((5(√3))/6)) J=∫_0 ^1 (−2x−1)dx=−x^2 −x]_0 ^1 = (−1−1)−0=−2 ∫_0 ^1 f(x)dx=I+J=((−7)/4)+(1/2)ln(((5(√3))/6))
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}^{\mathrm{2}} +\mathrm{3}}{dx} \\ $$$${x}=\sqrt{\mathrm{3}}{tg}\alpha\Rightarrow{dx}=\sqrt{\mathrm{3}}{sec}^{\mathrm{2}} \alpha{d}\alpha \\ $$$$\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}=\sqrt{\mathrm{3}}{sec}\alpha \\ $$$$\begin{cases}{{x}=\mathrm{0}\Rightarrow\alpha=\mathrm{0}}\\{{x}=\mathrm{1}\Rightarrow\alpha=\frac{\pi}{\mathrm{6}}}\end{cases}\Rightarrow \\ $$$${I}=\mathrm{3}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} {sec}^{\mathrm{3}} \alpha{d}\alpha= \\ $$$$\left.\frac{\mathrm{1}}{\mathrm{2}}{sec}\alpha{tg}\alpha+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{sec}\alpha+{tg}\alpha\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} = \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\right)−\mathrm{0}= \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{6}}\right) \\ $$$$\left.{J}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{2}{x}−\mathrm{1}\right){dx}=−{x}^{\mathrm{2}} −{x}\right]_{\mathrm{0}} ^{\mathrm{1}} = \\ $$$$\left(−\mathrm{1}−\mathrm{1}\right)−\mathrm{0}=−\mathrm{2} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}={I}+{J}=\frac{−\mathrm{7}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{6}}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by kaivan.ahmadi last updated on 24/Mar/19
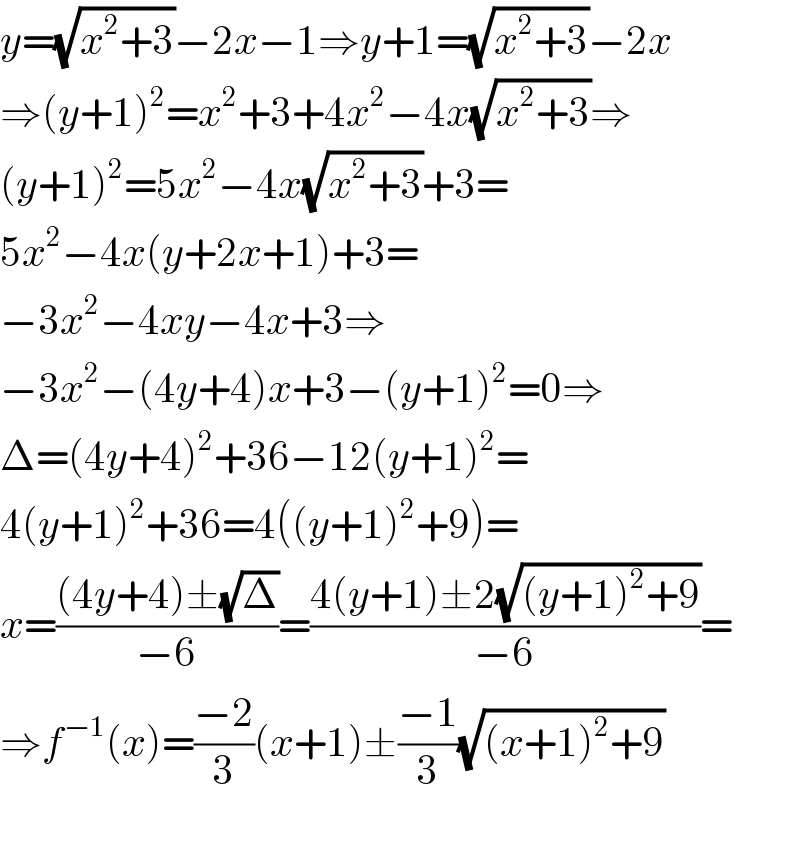
y=(√(x^2 +3))−2x−1⇒y+1=(√(x^2 +3))−2x ⇒(y+1)^2 =x^2 +3+4x^2 −4x(√(x^2 +3))⇒ (y+1)^2 =5x^2 −4x(√(x^2 +3))+3= 5x^2 −4x(y+2x+1)+3= −3x^2 −4xy−4x+3⇒ −3x^2 −(4y+4)x+3−(y+1)^2 =0⇒ Δ=(4y+4)^2 +36−12(y+1)^2 = 4(y+1)^2 +36=4((y+1)^2 +9)= x=(((4y+4)±(√Δ))/(−6))=((4(y+1)±2(√((y+1)^2 +9)))/(−6))= ⇒f^(−1) (x)=((−2)/3)(x+1)±((−1)/3)(√((x+1)^2 +9))
$${y}=\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}−\mathrm{2}{x}−\mathrm{1}\Rightarrow{y}+\mathrm{1}=\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}−\mathrm{2}{x} \\ $$$$\Rightarrow\left({y}+\mathrm{1}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +\mathrm{3}+\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\Rightarrow \\ $$$$\left({y}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{5}{x}^{\mathrm{2}} −\mathrm{4}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}+\mathrm{3}= \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{4}{x}\left({y}+\mathrm{2}{x}+\mathrm{1}\right)+\mathrm{3}= \\ $$$$−\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}{xy}−\mathrm{4}{x}+\mathrm{3}\Rightarrow \\ $$$$−\mathrm{3}{x}^{\mathrm{2}} −\left(\mathrm{4}{y}+\mathrm{4}\right){x}+\mathrm{3}−\left({y}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow \\ $$$$\Delta=\left(\mathrm{4}{y}+\mathrm{4}\right)^{\mathrm{2}} +\mathrm{36}−\mathrm{12}\left({y}+\mathrm{1}\right)^{\mathrm{2}} = \\ $$$$\mathrm{4}\left({y}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{36}=\mathrm{4}\left(\left({y}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{9}\right)= \\ $$$${x}=\frac{\left(\mathrm{4}{y}+\mathrm{4}\right)\pm\sqrt{\Delta}}{−\mathrm{6}}=\frac{\mathrm{4}\left({y}+\mathrm{1}\right)\pm\mathrm{2}\sqrt{\left({y}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{9}}}{−\mathrm{6}}= \\ $$$$\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\frac{−\mathrm{2}}{\mathrm{3}}\left({x}+\mathrm{1}\right)\pm\frac{−\mathrm{1}}{\mathrm{3}}\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{9}} \\ $$$$ \\ $$
Commented by Abdo msup. last updated on 25/Mar/19
sir Ahmadi wher are you from....
$${sir}\:{Ahmadi}\:{wher}\:{are}\:{you}\:{from}…. \\ $$
Commented by kaivan.ahmadi last updated on 25/Mar/19
Hi dear Abdo, i′m Iranian
$${Hi}\:{dear}\:{Abdo},\:{i}'{m}\:{Iranian} \\ $$
Commented by maxmathsup by imad last updated on 25/Mar/19
wich you good luck sir i hope to visit Iran somedays....
$${wich}\:{you}\:{good}\:{luck}\:{sir}\:{i}\:{hope}\:{to}\:{visit}\:{Iran}\:{somedays}…. \\ $$
Commented by maxmathsup by imad last updated on 26/Mar/19
1) ∫_0 ^1 f(x)dx =∫_0 ^1 (√(x^2 +3))dx −∫_0 ^1 (2x+1)dx ∫_0 ^1 (2x+1)dx =[x^2 +x]_0 ^1 =2 ∫_0 ^1 (√(x^2 +3))dx =_(x=(√3)sh(t)) ∫_0 ^(arsh((1/( (√3))))) (√3)ch(t)(√3)ch(t)dt =3 ∫_0 ^(argsh((1/( (√3))))) ((1+ch(2t))/2)dt =(3/2) argsh((1/( (√3)))) +(3/4) [sh(2t)]_0 ^(argsh((1/( (√3))))) =(3/2)ln((1/( (√3))) +(√(4/3))) +(3/8)[e^(2t) −e^(−2t) ]_0 ^(argsh((1/( (√3))))) =(3/2)ln((√3)) +(3/8){ 3−(1/3)} =(3/4)ln(3) +1 ⇒∫_0 ^1 f(x)dx =(3/4)ln(3)−1 .
$$\left.\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}^{\mathrm{2}} +\mathrm{3}}{dx}\:−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{x}+\mathrm{1}\right){dx}\:\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{x}+\mathrm{1}\right){dx}\:=\left[{x}^{\mathrm{2}} \:+{x}\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{2} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}^{\mathrm{2}} \:+\mathrm{3}}{dx}\:=_{{x}=\sqrt{\mathrm{3}}{sh}\left({t}\right)} \:\:\:\int_{\mathrm{0}} ^{{arsh}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)} \sqrt{\mathrm{3}}{ch}\left({t}\right)\sqrt{\mathrm{3}}{ch}\left({t}\right){dt}\:=\mathrm{3}\:\int_{\mathrm{0}} ^{{argsh}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)} \frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}{dt} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\:{argsh}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+\frac{\mathrm{3}}{\mathrm{4}}\:\left[{sh}\left(\mathrm{2}{t}\right)\right]_{\mathrm{0}} ^{{argsh}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)} =\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:+\sqrt{\frac{\mathrm{4}}{\mathrm{3}}}\right)\:+\frac{\mathrm{3}}{\mathrm{8}}\left[{e}^{\mathrm{2}{t}} −{e}^{−\mathrm{2}{t}} \right]_{\mathrm{0}} ^{{argsh}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\sqrt{\mathrm{3}}\right)\:+\frac{\mathrm{3}}{\mathrm{8}}\left\{\:\mathrm{3}−\frac{\mathrm{1}}{\mathrm{3}}\right\}\:=\frac{\mathrm{3}}{\mathrm{4}}{ln}\left(\mathrm{3}\right)\:+\mathrm{1}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\:=\frac{\mathrm{3}}{\mathrm{4}}{ln}\left(\mathrm{3}\right)−\mathrm{1}\:. \\ $$
Commented by kaivan.ahmadi last updated on 26/Mar/19
thank sir,where are you from?
$${thank}\:{sir},{where}\:{are}\:{you}\:{from}? \\ $$
Commented by maxmathsup by imad last updated on 26/Mar/19
i am from morocco sir.
$${i}\:{am}\:{from}\:{morocco}\:{sir}. \\ $$
Commented by maxmathsup by imad last updated on 30/Mar/19
2) f(x)=y ⇔x =f^(−1) (y) and f(x)=y ⇒(√(x^2 +3))−2x−1=y ⇒ (2x+1+y)=(√(x^2 +3)) ⇒(2x+1+y)^2 =x^2 +3 ⇒ (2x+1)^2 +2(2x+1)y +y^2 =x^2 +3 ⇒ 4x^2 +4x +1 +4yx +2y +y^2 −x^2 −3 =0 ⇒ 3x^2 +(4+4y)x +y^2 +2y−2 =0 let find x interms of y Δ^, =(2+2y)^2 −3(y^2 +2y−2) =4 +8y +4y^2 −3y^2 −6y +6 =y^2 +2y +10 =(y+1)^2 +9 ⇒ x_1 =((−2(y+1) +(√((y+1)^2 +9)))/3) x_2 =((−2(y+1) −(√((y+1)^2 +9)))/3) we must have 2x+1+y≥0 let verify this condition 2x_1 +1 +y =((−4y−4 +2(√((y+1)^2 +9))+3+3y)/3)=((2(√(y^2 +2y +10))−y−1)/3) we have 4(y^2 +2y+10)−(y+1)^2 =4y^2 +6y +40−y^2 −2y−1 =3y^2 +4y +39> ⇒x_1 is the solution ⇒f^(−1) (x)=(((√((x+1)^2 +9))−2(x+1))/3)
$$\left.\mathrm{2}\right)\:{f}\left({x}\right)={y}\:\Leftrightarrow{x}\:={f}^{−\mathrm{1}} \left({y}\right)\:{and}\:{f}\left({x}\right)={y}\:\Rightarrow\sqrt{{x}^{\mathrm{2}} \:+\mathrm{3}}−\mathrm{2}{x}−\mathrm{1}={y}\:\Rightarrow \\ $$$$\left(\mathrm{2}{x}+\mathrm{1}+{y}\right)=\sqrt{{x}^{\mathrm{2}} \:+\mathrm{3}}\:\Rightarrow\left(\mathrm{2}{x}+\mathrm{1}+{y}\right)^{\mathrm{2}} \:={x}^{\mathrm{2}} \:+\mathrm{3}\:\Rightarrow \\ $$$$\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{2}\left(\mathrm{2}{x}+\mathrm{1}\right){y}\:+{y}^{\mathrm{2}} \:={x}^{\mathrm{2}} \:+\mathrm{3}\:\Rightarrow \\ $$$$\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:+\mathrm{1}\:+\mathrm{4}{yx}\:+\mathrm{2}{y}\:+{y}^{\mathrm{2}} \:−{x}^{\mathrm{2}} −\mathrm{3}\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{3}{x}^{\mathrm{2}} \:+\left(\mathrm{4}+\mathrm{4}{y}\right){x}\:+{y}^{\mathrm{2}} \:+\mathrm{2}{y}−\mathrm{2}\:=\mathrm{0}\:\:{let}\:{find}\:{x}\:{interms}\:{of}\:{y} \\ $$$$\Delta^{,} \:=\left(\mathrm{2}+\mathrm{2}{y}\right)^{\mathrm{2}} −\mathrm{3}\left({y}^{\mathrm{2}} \:+\mathrm{2}{y}−\mathrm{2}\right)\:=\mathrm{4}\:+\mathrm{8}{y}\:+\mathrm{4}{y}^{\mathrm{2}} \:−\mathrm{3}{y}^{\mathrm{2}} \:−\mathrm{6}{y}\:+\mathrm{6} \\ $$$$={y}^{\mathrm{2}} \:+\mathrm{2}{y}\:\:+\mathrm{10}\:\:=\left({y}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{9}\:\Rightarrow\:{x}_{\mathrm{1}} =\frac{−\mathrm{2}\left({y}+\mathrm{1}\right)\:+\sqrt{\left({y}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{9}}}{\mathrm{3}} \\ $$$${x}_{\mathrm{2}} =\frac{−\mathrm{2}\left({y}+\mathrm{1}\right)\:−\sqrt{\left({y}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{9}}}{\mathrm{3}}\:\:\:{we}\:{must}\:{have}\:\mathrm{2}{x}+\mathrm{1}+{y}\geqslant\mathrm{0}\:{let}\:{verify}\:{this} \\ $$$${condition} \\ $$$$\mathrm{2}{x}_{\mathrm{1}} +\mathrm{1}\:+{y}\:=\frac{−\mathrm{4}{y}−\mathrm{4}\:+\mathrm{2}\sqrt{\left({y}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{9}}+\mathrm{3}+\mathrm{3}{y}}{\mathrm{3}}=\frac{\mathrm{2}\sqrt{{y}^{\mathrm{2}} \:+\mathrm{2}{y}\:+\mathrm{10}}−{y}−\mathrm{1}}{\mathrm{3}} \\ $$$${we}\:{have}\:\mathrm{4}\left({y}^{\mathrm{2}} \:+\mathrm{2}{y}+\mathrm{10}\right)−\left({y}+\mathrm{1}\right)^{\mathrm{2}} \:=\mathrm{4}{y}^{\mathrm{2}} \:+\mathrm{6}{y}\:+\mathrm{40}−{y}^{\mathrm{2}} \:−\mathrm{2}{y}−\mathrm{1} \\ $$$$=\mathrm{3}{y}^{\mathrm{2}} \:+\mathrm{4}{y}\:+\mathrm{39}>\:\Rightarrow{x}_{\mathrm{1}} {is}\:{the}\:{solution}\:\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\frac{\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{9}}−\mathrm{2}\left({x}+\mathrm{1}\right)}{\mathrm{3}} \\ $$
Commented by maxmathsup by imad last updated on 30/Mar/19
∫ f^(−1) (x)dx =(1/3) ∫ (√((x+1)^2 +9))dx −(2/3) ∫ (x+1)dx ∫ (x+1)dx =(x^2 /2) +x +c_1 ∫ (√((x+1)^2 +9))dx =_(x+1=3 sh(t)) ∫ 3ch(t)3ch(t) =9 ∫ ch^2 t dt =9 ∫ ((1+ch(2t))/2) dt =(9/2) t +(9/4) sh(2t) =(9/2)t +(9/2) ch(t)sh(t) +c_2 =(9/2) argsh(((x+1)/3)) +(9/2) ((x+1)/3) (√(1+(((x+1)/3))^2 )) =(9/2)ln(((x+1)/3) +(√(1+(((x+1)/3))^2 )) ) +(3/2)(x+1) (√(1+(((x+1)/3))^2 )) +c_2 ⇒ ∫ f^(−1) (x)dx = (3/z)ln(((x+1)/3) +(√(1+(((x+1)/3))^2 ))) +((x+1)/2)(√(1+(((x+1)/3))^2 )) −(1/3)x^2 −(2/3)x +C
$$\int\:{f}^{−\mathrm{1}} \left({x}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{3}}\:\int\:\:\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{9}}{dx}\:−\frac{\mathrm{2}}{\mathrm{3}}\:\int\:\:\left({x}+\mathrm{1}\right){dx} \\ $$$$\int\:\left({x}+\mathrm{1}\right){dx}\:=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+{x}\:+{c}_{\mathrm{1}} \\ $$$$\int\:\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{9}}{dx}\:=_{{x}+\mathrm{1}=\mathrm{3}\:{sh}\left({t}\right)} \:\:\:\int\:\mathrm{3}{ch}\left({t}\right)\mathrm{3}{ch}\left({t}\right)\:=\mathrm{9}\:\int\:{ch}^{\mathrm{2}} {t}\:{dt} \\ $$$$=\mathrm{9}\:\int\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\:{dt}\:=\frac{\mathrm{9}}{\mathrm{2}}\:{t}\:\:+\frac{\mathrm{9}}{\mathrm{4}}\:{sh}\left(\mathrm{2}{t}\right)\:=\frac{\mathrm{9}}{\mathrm{2}}{t}\:+\frac{\mathrm{9}}{\mathrm{2}}\:{ch}\left({t}\right){sh}\left({t}\right)\:+{c}_{\mathrm{2}} \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\:{argsh}\left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)\:+\frac{\mathrm{9}}{\mathrm{2}}\:\frac{{x}+\mathrm{1}}{\mathrm{3}}\:\sqrt{\mathrm{1}+\left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}{ln}\left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\:+\sqrt{\mathrm{1}+\left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }\:\right)\:\:+\frac{\mathrm{3}}{\mathrm{2}}\left({x}+\mathrm{1}\right)\:\sqrt{\mathrm{1}+\left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }\:+{c}_{\mathrm{2}} \:\Rightarrow \\ $$$$\int\:{f}^{−\mathrm{1}} \left({x}\right){dx}\:=\:\frac{\mathrm{3}}{{z}}{ln}\left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\:+\sqrt{\mathrm{1}+\left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }\right)\:\:+\frac{{x}+\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}+\left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{2}} \:−\frac{\mathrm{2}}{\mathrm{3}}{x}\:+{C} \\ $$
Answered by MJS last updated on 25/Mar/19
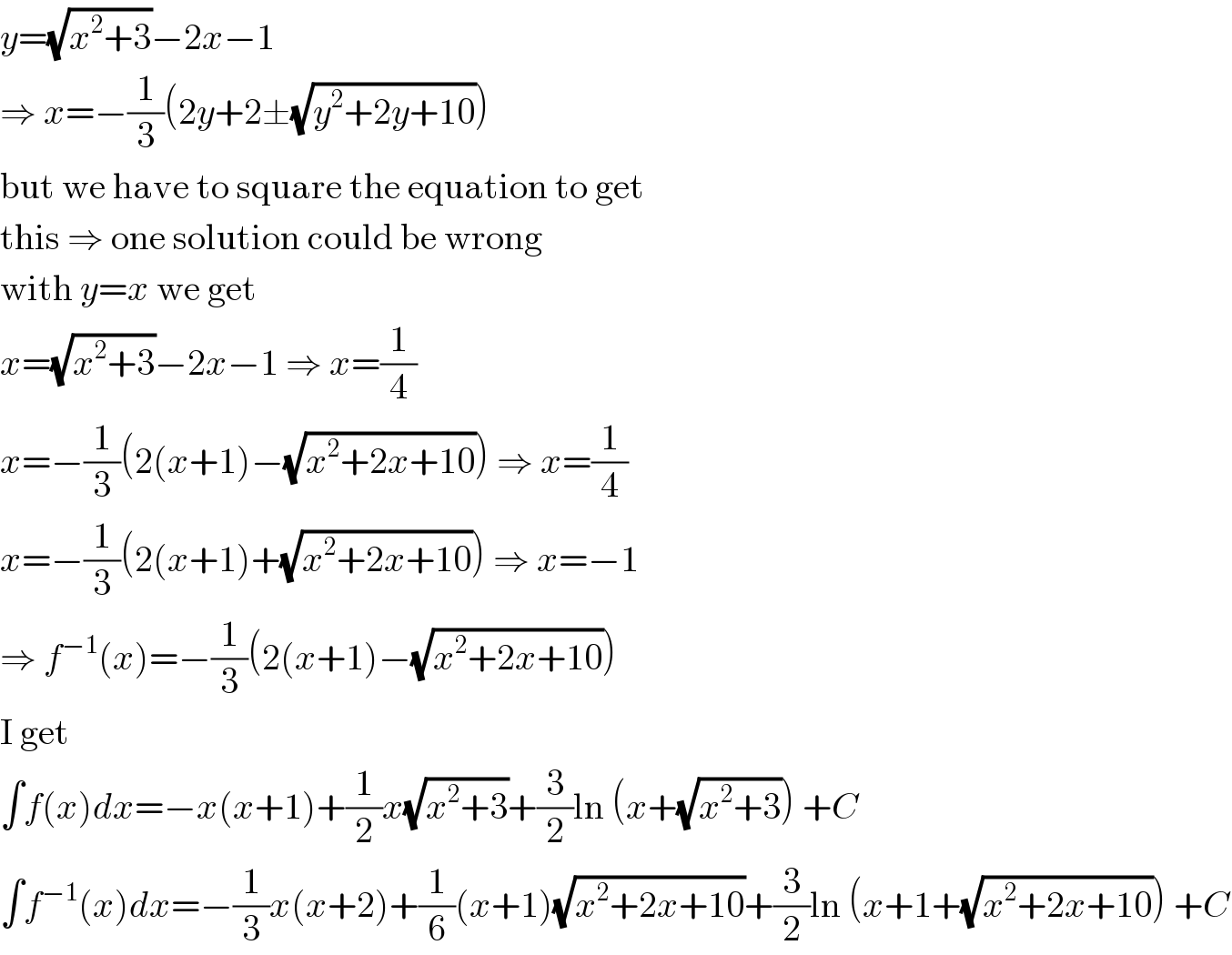
y=(√(x^2 +3))−2x−1 ⇒ x=−(1/3)(2y+2±(√(y^2 +2y+10))) but we have to square the equation to get this ⇒ one solution could be wrong with y=x we get x=(√(x^2 +3))−2x−1 ⇒ x=(1/4) x=−(1/3)(2(x+1)−(√(x^2 +2x+10))) ⇒ x=(1/4) x=−(1/3)(2(x+1)+(√(x^2 +2x+10))) ⇒ x=−1 ⇒ f^(−1) (x)=−(1/3)(2(x+1)−(√(x^2 +2x+10))) I get ∫f(x)dx=−x(x+1)+(1/2)x(√(x^2 +3))+(3/2)ln (x+(√(x^2 +3))) +C ∫f^(−1) (x)dx=−(1/3)x(x+2)+(1/6)(x+1)(√(x^2 +2x+10))+(3/2)ln (x+1+(√(x^2 +2x+10))) +C
$${y}=\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}−\mathrm{2}{x}−\mathrm{1} \\ $$$$\Rightarrow\:{x}=−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}{y}+\mathrm{2}\pm\sqrt{{y}^{\mathrm{2}} +\mathrm{2}{y}+\mathrm{10}}\right) \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{square}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{to}\:\mathrm{get} \\ $$$$\mathrm{this}\:\Rightarrow\:\mathrm{one}\:\mathrm{solution}\:\mathrm{could}\:\mathrm{be}\:\mathrm{wrong} \\ $$$$\mathrm{with}\:{y}={x}\:\mathrm{we}\:\mathrm{get} \\ $$$${x}=\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}−\mathrm{2}{x}−\mathrm{1}\:\Rightarrow\:{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}\left({x}+\mathrm{1}\right)−\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}}\right)\:\Rightarrow\:{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}\left({x}+\mathrm{1}\right)+\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}}\right)\:\Rightarrow\:{x}=−\mathrm{1} \\ $$$$\Rightarrow\:{f}^{−\mathrm{1}} \left({x}\right)=−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}\left({x}+\mathrm{1}\right)−\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}}\right) \\ $$$$\mathrm{I}\:\mathrm{get} \\ $$$$\int{f}\left({x}\right){dx}=−{x}\left({x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)\:+{C} \\ $$$$\int{f}^{−\mathrm{1}} \left({x}\right){dx}=−\frac{\mathrm{1}}{\mathrm{3}}{x}\left({x}+\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{6}}\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\:\left({x}+\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}}\right)\:+{C} \\ $$
Commented by kaivan.ahmadi last updated on 25/Mar/19
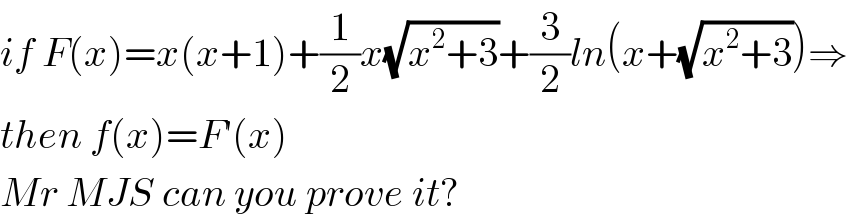
if F(x)=x(x+1)+(1/2)x(√(x^2 +3))+(3/2)ln(x+(√(x^2 +3)))⇒ then f(x)=F′(x) Mr MJS can you prove it?
$${if}\:{F}\left({x}\right)={x}\left({x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{2}}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)\Rightarrow \\ $$$${then}\:{f}\left({x}\right)={F}'\left({x}\right) \\ $$$${Mr}\:{MJS}\:{can}\:{you}\:{prove}\:{it}? \\ $$
Commented by maxmathsup by imad last updated on 25/Mar/19
thanks sir .
$${thanks}\:{sir}\:. \\ $$
Commented by MJS last updated on 25/Mar/19
F(x)=−x(x+1)+(1/2)x(√(x^2 +3))+(3/2)ln (x+(√(x^2 +3))) F′(x)=(d/dx)[−x(x+1)]+(d/dx)[(1/2)x(√(x^2 +3))]+(d/dx)[(3/2)ln (x+(√(x^2 +3)))] (d/dx)[−x(x+1)]=−2x−1 (d/dx)[(1/2)x(√(x^2 +3))]=(1/2)((√(x^2 +3))+(x^2 /( (√(x^2 +3)))))=((2x^2 +3)/(2(√(x^2 +3)))) (d/dx)[(3/2)ln (x+(√(x^2 +3)))]=(3/2)((1/(x+(√(x^2 +3))))(1+(x/( (√(x^2 +3))))))= =(3/2)(((x−(√(x^2 +3)))/(−3))×((x+(√(x^2 +3)))/( (√(x^2 +3)))))=(3/(2(√(x^2 +3)))) −2x−1+((2x^2 +3)/(2(√(x^2 +3))))+(3/(2(√(x^2 +3))))= −2x−1+((2x^2 +6)/(2(√(x^2 +3))))=−2x−1+((x^2 +3)/( (√(x^2 +3))))= =(√(x^2 +3))−2x−1
$${F}\left({x}\right)=−{x}\left({x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right) \\ $$$${F}'\left({x}\right)=\frac{{d}}{{dx}}\left[−{x}\left({x}+\mathrm{1}\right)\right]+\frac{{d}}{{dx}}\left[\frac{\mathrm{1}}{\mathrm{2}}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right]+\frac{{d}}{{dx}}\left[\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)\right] \\ $$$$\frac{{d}}{{dx}}\left[−{x}\left({x}+\mathrm{1}\right)\right]=−\mathrm{2}{x}−\mathrm{1} \\ $$$$\frac{{d}}{{dx}}\left[\frac{\mathrm{1}}{\mathrm{2}}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right]=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}+\frac{{x}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}\right)=\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}} \\ $$$$\frac{{d}}{{dx}}\left[\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)\right]=\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}\left(\mathrm{1}+\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}\right)\right)= \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{{x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{−\mathrm{3}}×\frac{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}\right)=\frac{\mathrm{3}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}} \\ $$$$−\mathrm{2}{x}−\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}+\frac{\mathrm{3}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}= \\ $$$$−\mathrm{2}{x}−\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}=−\mathrm{2}{x}−\mathrm{1}+\frac{{x}^{\mathrm{2}} +\mathrm{3}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}= \\ $$$$=\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}−\mathrm{2}{x}−\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *