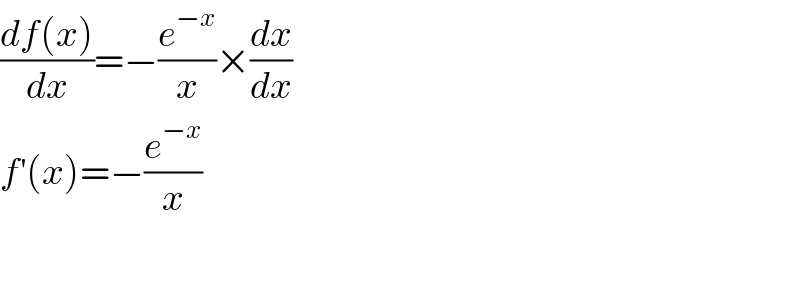Question Number 44318 by abdo.msup.com last updated on 26/Sep/18
$${let}\:{f}\left({x}\right)=\int_{{x}} ^{+\infty} \:\frac{{e}^{−{t}} }{{t}}{dt} \\ $$$$\left.\mathrm{1}\right){calculate}\:{f}^{'} \left({x}\right) \\ $$$$\left.\mathrm{2}\right){find}\:{a}\:{equivalent}\:{of}\:{f}\left({x}\right)\:{when} \\ $$$${x}\rightarrow+\infty. \\ $$
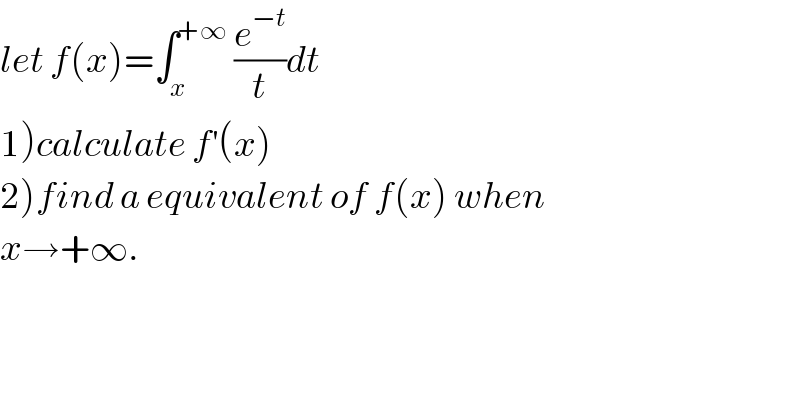
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Sep/18
Commented by maxmathsup by imad last updated on 27/Sep/18
![we have f(x) = ∫_x ^1 (e^(−t) /t)dt +∫_1 ^(+∞) (e^(−t) /t)dt =∫_1 ^(+∞) (e^(−t) /t)dt−∫_1 ^x (e^(−t) /t)dt ⇒ f^′ (x)= −(e^(−x) /x) (x>0) 2) let integrate by parts f(x) =[ −(e^(−t) /t)]_x ^(+∞) −∫_x ^(+∞) (e^(−t) /t^2 ) dt = (e^(−x) /x) − ∫_x ^(+∞) (e^(−t) /t^2 )dt ⇒ ∣f(x)−(e^(−x) /x)∣ =∣ ∫_x ^(+∞) (e^(−t) /t^2 )dt∣ ≤ ∫_x ^(+∞) (dt/t^2 ) =[−(1/t)]_x ^(+∞) =(1/x) →0(x→+∞) ⇒ f(x)∼ (e^(−x) /x) (x→+∞).](https://www.tinkutara.com/question/Q44354.png)
$${we}\:{have}\:{f}\left({x}\right)\:=\:\int_{{x}} ^{\mathrm{1}} \:\frac{{e}^{−{t}} }{{t}}{dt}\:\:+\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{{e}^{−{t}} }{{t}}{dt}\:=\int_{\mathrm{1}} ^{+\infty} \:\frac{{e}^{−{t}} }{{t}}{dt}−\int_{\mathrm{1}} ^{{x}} \:\:\frac{{e}^{−{t}} }{{t}}{dt}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)=\:−\frac{{e}^{−{x}} }{{x}}\:\:\left({x}>\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\:{let}\:{integrate}\:{by}\:{parts}\: \\ $$$${f}\left({x}\right)\:=\left[\:−\frac{{e}^{−{t}} }{{t}}\right]_{{x}} ^{+\infty} \:−\int_{{x}} ^{+\infty} \:\frac{{e}^{−{t}} }{{t}^{\mathrm{2}} }\:{dt}\:=\:\frac{{e}^{−{x}} }{{x}}\:−\:\int_{{x}} ^{+\infty} \:\:\frac{{e}^{−{t}} }{{t}^{\mathrm{2}} }{dt}\:\Rightarrow \\ $$$$\mid{f}\left({x}\right)−\frac{{e}^{−{x}} }{{x}}\mid\:=\mid\:\int_{{x}} ^{+\infty} \:\:\frac{{e}^{−{t}} }{{t}^{\mathrm{2}} }{dt}\mid\:\leqslant\:\int_{{x}} ^{+\infty} \:\:\frac{{dt}}{{t}^{\mathrm{2}} }\:=\left[−\frac{\mathrm{1}}{{t}}\right]_{{x}} ^{+\infty} =\frac{\mathrm{1}}{{x}}\:\rightarrow\mathrm{0}\left({x}\rightarrow+\infty\right)\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\:\frac{{e}^{−{x}} }{{x}}\:\:\left({x}\rightarrow+\infty\right). \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Sep/18
$$\frac{{df}\left({x}\right)}{{dx}}=−\frac{{e}^{−{x}} }{{x}}×\frac{{dx}}{{dx}} \\ $$$${f}^{'} \left({x}\right)=−\frac{{e}^{−{x}} }{{x}} \\ $$$$ \\ $$