let-f-x-x-x-1-1-find-D-f-2-give-the-equation-of-assymtote-at-point-A-0-f-o-3-if-f-x-a-x-1-b-x-1-determine-a-andb-4-calculate-f-x-5-find-f-1-x-and-f-1-

Question Number 37892 by abdo mathsup 649 cc last updated on 19/Jun/18

l e t f (x) = \sqrt{x + \sqrt{x + 1}}

1) f i n d D_{f}

2) g i v e t h e e q u a t i o n o f a s s y m t o t e a t p o i n t

A (0, f (o))

3) i f f (x) \sim a (x - 1) + b (x \to 1) d e t e r m i n e a a n d b

4) c a l c u l a t e f^{^{'}} (x)

5) f i n d f^{- 1} (x) a n d {(f^{- 1})}^{^{'}} (x)

Commented by prof Abdo imad last updated on 21/Jun/18

4) w e h a v e f^{2} (x) = x + \sqrt{x + 1} \Rightarrow

2 f (x) f^{^{'}} (x) = 1 + \frac{1}{2 \sqrt{x + 1}} \Rightarrow

2 \sqrt{x + \sqrt{x + 1}} f^{^{'}} (x) = 1 + \frac{1}{2 \sqrt{x + 1}} \Rightarrow

f^{^{'}} (x) = \frac{1}{2 \sqrt{x + \sqrt{x + 1}}} {1 + \frac{1}{2 \sqrt{x + 1}}}

5) l e t f (x) = y \Leftrightarrow x = f^{- 1} (y) \Rightarrow

\sqrt{x + \sqrt{x + 1}} = y \Rightarrow x + \sqrt{x + 1} = y^{2} \Rightarrow

\sqrt{x + 1} = y^{2} - x \Rightarrow x + 1 = {(y^{2} - x)}^{2} = x + 1 \Rightarrow

x^{2} - 2 y^{2} x + y^{4} - x - 1 = 0 \Rightarrow x^{2} - (2 y^{2} + 1) x + y^{4} - 1 = 0

Δ = {(2 y^{2} + 1)}^{2} - 4 (y^{4} - 1)

= 4 y^{4} + 4 y^{2} + 1 - 4 y^{4} + 4 = 4 y^{2} + 5 > 0

x_{1} = \frac{2 y^{2} + 1 + \sqrt{4 y^{2} + 5}}{2}

x_{2} = \frac{2 y^{2} + 1 - \sqrt{4 y^{2} + 5}}{2} b u t w e m u s t h a v e

x + 1 ⩾ 0 a n d y^{2} - x ⩾ 0 a f t e r v e r i f i c a t i o n

w e f i n d t h a t x = \frac{2 y^{2} + 1 - \sqrt{4 y^{2} + 5}}{2} \Rightarrow

f^{- 1} (x) = \frac{2 x^{2} + 1 - \sqrt{4 x^{2} + 5}}{2} s o

{(f^{- 1})}^{^{'}} (x) = 2 x - \frac{1}{2} \frac{8 x}{2 \sqrt{4 x^{2} + 5}}

= 2 x - \frac{4 x}{\sqrt{4 x^{2} + 5}} .

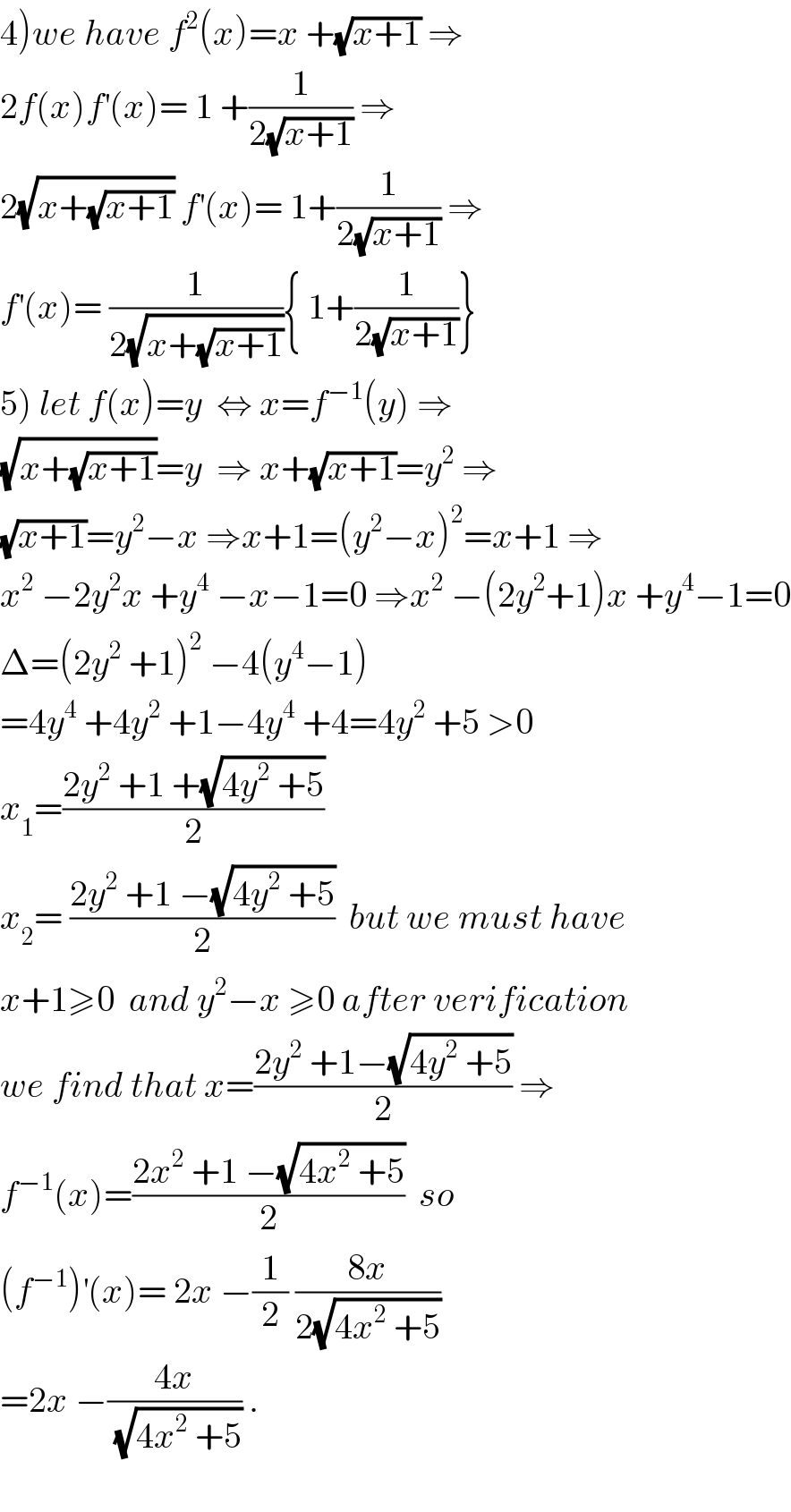
Commented by math khazana by abdo last updated on 21/Jun/18

1) x \in D_{f} \Leftrightarrow x + 1 ⩾ 0 a n d x + \sqrt{x + 1} ⩾ 0 \Rightarrow

x ⩾ - 1 a n d x + \sqrt{x + 1} ⩾ 0 s o i f x ⩾ 0 w e g e t

x + \sqrt{x + 1} > 0 i f - 1 ⩽ x ⩽ 0

\sqrt{x + 1} + x = \sqrt{x + 1} - (- x) a n d

{(\sqrt{x + 1})}^{2} - {(- x)}^{2} = x + 1 - x^{2}

= - x^{2} + x + 1 \Rightarrow Δ = 1 - 4 (- 1) = 5

x_{1} = \frac{- 1 + \sqrt{5}}{2} {a n d x}_{2} = \frac{- 1 - \sqrt{5}}{2}

\sqrt{x + 1} + x = \frac{x + 1 - x^{2}}{\sqrt{x + 1} - x} a n d \sqrt{x + 1} - x > 0 s o

\sqrt{1 + x} + x ⩾ 0 \Leftrightarrow x \in [\frac{- 1 - \sqrt{5}}{2}, \frac{- 1 + \sqrt{5}}{2}] b u t

[- 1, 0] \subset [\frac{- 1 - \sqrt{5}}{2}, \frac{- 1 + \sqrt{5}}{2}] \Rightarrow D_{f} = [- 1, + \infty [

2) y = f^{^{'}} (0) x + f (0) b u t f (x) = \sqrt{x + \sqrt{x + 1}} \Rightarrow

f (0) = 1 w e h a v e f^{2} (x) = x + \sqrt{x + 1} \Rightarrow

2 f (x) f^{^{'}} (x) = 1 + \frac{1}{2 \sqrt{x + 1}} \Rightarrow 2 f (0) f^{^{'}} (0) = \frac{3}{2} \Rightarrow

f^{^{'}} (0) = \frac{3}{4} s o t h e e q u a t i o n o f a s s y m p t o t e i s

y = \frac{3}{4} x + 1 .

Commented by math khazana by abdo last updated on 21/Jun/18

3) w e h a v e a = f^{^{'}} (1) a n d b = f (1)

b = \sqrt{1 + \sqrt{2}}

2 f (1) f^{^{'}} (1) = 1 + \frac{1}{2 \sqrt{2}} \Rightarrow f^{^{'}} (1) = \frac{1}{2 \sqrt{1 + \sqrt{2}}} (1 + \frac{1}{2 \sqrt{2}}) = a