Question Number 35052 by math khazana by abdo last updated on 14/May/18
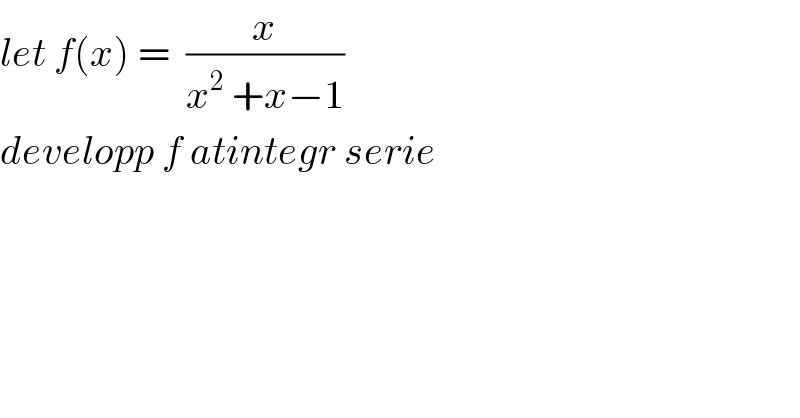
$${let}\:{f}\left({x}\right)\:=\:\:\frac{{x}}{{x}^{\mathrm{2}} \:+{x}−\mathrm{1}} \\ $$$${developp}\:{f}\:{atintegr}\:{serie} \\ $$
Commented by abdo mathsup 649 cc last updated on 16/May/18

$${let}\:{find}\:{the}\:{roots}\:{of}\:{x}^{\mathrm{2}} \:+{x}−\mathrm{1} \\ $$$$\Delta=\mathrm{1}−\mathrm{4}\left(−\mathrm{1}\right)=\mathrm{5}\:\Rightarrow\:{x}_{\mathrm{1}} =\:\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:{and}\:\:{x}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${f}\left({x}\right)=\:\frac{{x}}{\left({x}\:−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right)}\:=\frac{{x}}{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }\left\{\:\frac{\mathrm{1}}{{x}−{x}_{\mathrm{2}} }\:−\frac{\mathrm{1}}{{x}−{x}_{\mathrm{1}} }\right\} \\ $$$$=\:\frac{{x}}{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }\left\{\:\:\:\frac{−\mathrm{1}}{{x}_{\mathrm{2}} \left(\mathrm{1}−\frac{{x}}{{x}_{\mathrm{2}} }\right)}\:+\:\frac{\mathrm{1}}{{x}_{\mathrm{1}} \left(\mathrm{1}−\frac{{x}}{{x}_{\mathrm{1}} }\right)}\right\}\:{so}\:\:{for} \\ $$$$\mid{x}\mid<{inf}\left(\:\mid{x}_{\mathrm{1}} \mid,\mid{x}_{\mathrm{2}} \mid\right)\:{we}\:{have} \\ $$$${f}\left({x}\right)=\:\frac{{x}}{−\sqrt{\mathrm{5}}}\left\{\:\frac{\mathrm{1}}{{x}_{\mathrm{1}} }\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{{x}}{{x}_{\mathrm{1}} }\right)^{{n}} \:\:−\frac{\mathrm{1}}{{x}_{\mathrm{2}} }\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{{x}}{{x}_{\mathrm{2}} }\right)^{{n}} \right\} \\ $$$${f}\left({x}\right)=\:\frac{{x}}{{x}_{\mathrm{2}} \sqrt{\mathrm{5}}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\left(\frac{{x}}{{x}_{\mathrm{2}} }\right)^{{n}} \:\:−\frac{{x}}{{x}_{\mathrm{1}} \sqrt{\mathrm{5}}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{{x}}{{x}_{\mathrm{1}} }\right)^{{n}} \:. \\ $$$$ \\ $$
