Question Number 36178 by prof Abdo imad last updated on 30/May/18
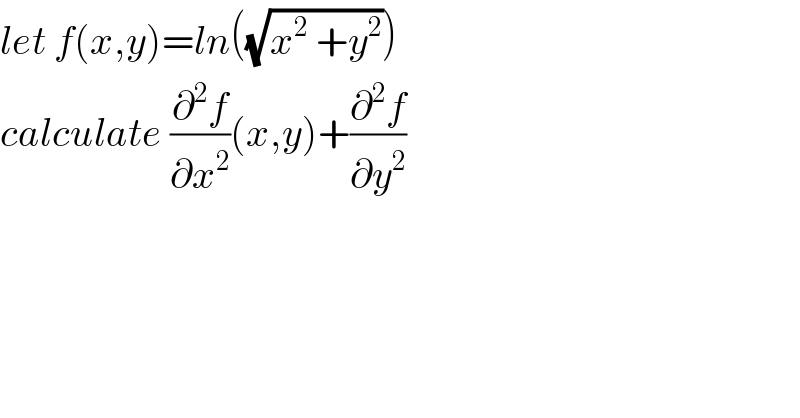
$${let}\:{f}\left({x},{y}\right)={ln}\left(\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\right)\: \\ $$$${calculate}\:\frac{\partial^{\mathrm{2}} {f}}{\partial{x}^{\mathrm{2}} }\left({x},{y}\right)+\frac{\partial^{\mathrm{2}} {f}}{\partial{y}^{\mathrm{2}} } \\ $$
Commented by abdo imad last updated on 31/May/18
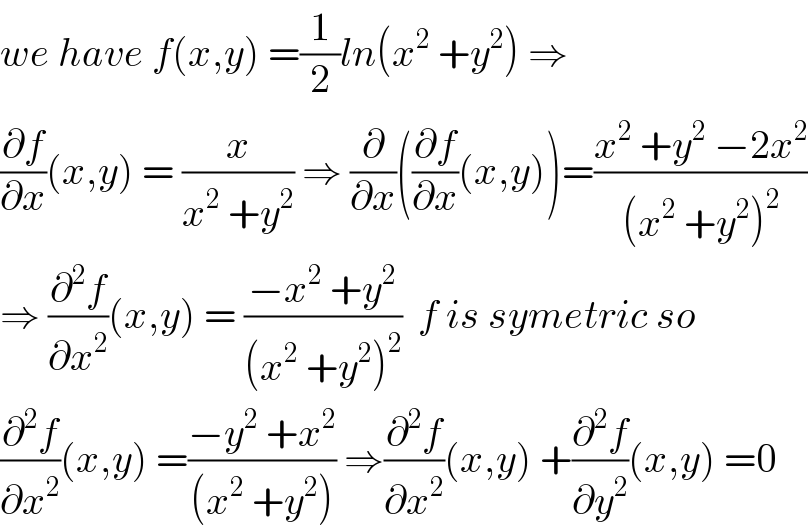
$${we}\:{have}\:{f}\left({x},{y}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\frac{\partial{f}}{\partial{x}}\left({x},{y}\right)\:=\:\frac{{x}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\:\Rightarrow\:\frac{\partial}{\partial{x}}\left(\frac{\partial{f}}{\partial{x}}\left({x},{y}\right)\right)=\frac{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:−\mathrm{2}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{\partial^{\mathrm{2}} {f}}{\partial{x}^{\mathrm{2}} }\left({x},{y}\right)\:=\:\frac{−{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:{f}\:{is}\:{symetric}\:{so} \\ $$$$\frac{\partial^{\mathrm{2}} {f}}{\partial{x}^{\mathrm{2}} }\left({x},{y}\right)\:=\frac{−{y}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)}\:\Rightarrow\frac{\partial^{\mathrm{2}} {f}}{\partial{x}^{\mathrm{2}} }\left({x},{y}\right)\:+\frac{\partial^{\mathrm{2}} {f}}{\partial{y}^{\mathrm{2}} }\left({x},{y}\right)\:=\mathrm{0} \\ $$
