Question Number 36179 by prof Abdo imad last updated on 30/May/18
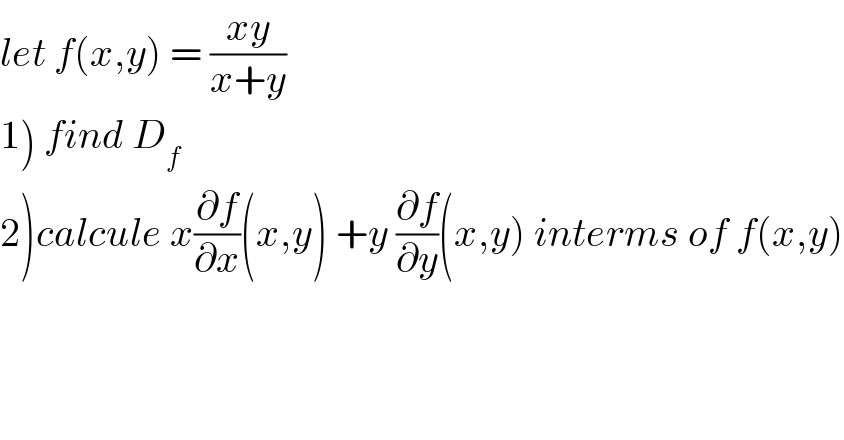
$${let}\:{f}\left({x},{y}\right)\:=\:\frac{{xy}}{{x}+{y}} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{D}_{{f}} \\ $$$$\left.\mathrm{2}\right){calcule}\:{x}\frac{\partial{f}}{\partial{x}}\left({x},{y}\right)\:+{y}\:\frac{\partial{f}}{\partial{y}}\left({x},{y}\right)\:{interms}\:{of}\:{f}\left({x},{y}\right) \\ $$
Commented by maxmathsup by imad last updated on 19/Aug/18
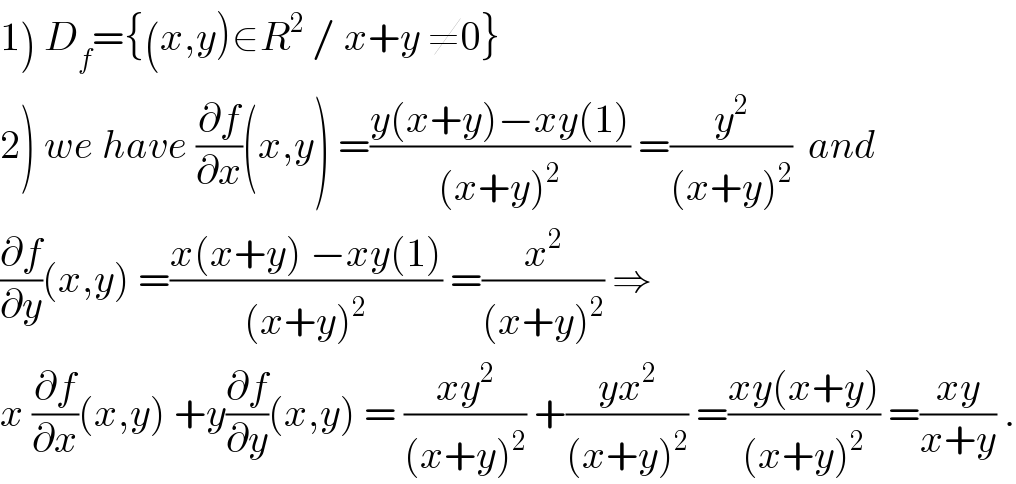
$$\left.\mathrm{1}\right)\:{D}_{{f}} =\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} \:/\:{x}+{y}\:\neq\mathrm{0}\right\} \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:\frac{\partial{f}}{\partial{x}}\left({x},{y}\right)\:=\frac{{y}\left({x}+{y}\right)−{xy}\left(\mathrm{1}\right)}{\left({x}+{y}\right)^{\mathrm{2}} }\:=\frac{{y}^{\mathrm{2}} }{\left({x}+{y}\right)^{\mathrm{2}} }\:\:{and} \\ $$$$\frac{\partial{f}}{\partial{y}}\left({x},{y}\right)\:=\frac{{x}\left({x}+{y}\right)\:−{xy}\left(\mathrm{1}\right)}{\left({x}+{y}\right)^{\mathrm{2}} }\:=\frac{{x}^{\mathrm{2}} }{\left({x}+{y}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${x}\:\frac{\partial{f}}{\partial{x}}\left({x},{y}\right)\:+{y}\frac{\partial{f}}{\partial{y}}\left({x},{y}\right)\:=\:\frac{{xy}^{\mathrm{2}} }{\left({x}+{y}\right)^{\mathrm{2}} }\:+\frac{{yx}^{\mathrm{2}} }{\left({x}+{y}\right)^{\mathrm{2}} }\:=\frac{{xy}\left({x}+{y}\right)}{\left({x}+{y}\right)^{\mathrm{2}} }\:=\frac{{xy}}{{x}+{y}}\:. \\ $$
