Question Number 63084 by mathmax by abdo last updated on 28/Jun/19
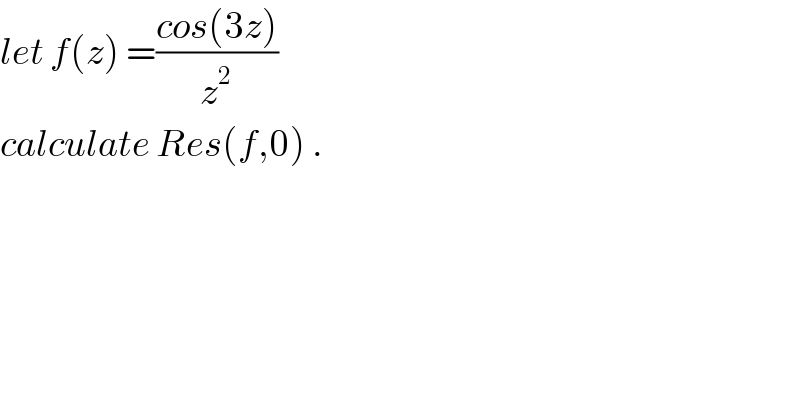
$${let}\:{f}\left({z}\right)\:=\frac{{cos}\left(\mathrm{3}{z}\right)}{{z}^{\mathrm{2}} } \\ $$$${calculate}\:{Res}\left({f},\mathrm{0}\right)\:. \\ $$
Commented by mathmax by abdo last updated on 01/Jul/19
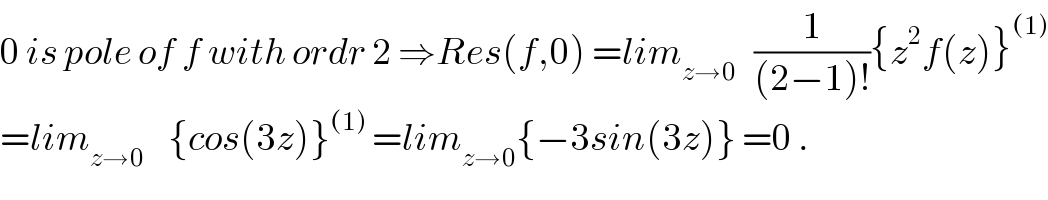
$$\mathrm{0}\:{is}\:{pole}\:{of}\:{f}\:{with}\:{ordr}\:\mathrm{2}\:\Rightarrow{Res}\left({f},\mathrm{0}\right)\:={lim}_{{z}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{{z}^{\mathrm{2}} {f}\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow\mathrm{0}} \:\:\:\:\left\{{cos}\left(\mathrm{3}{z}\right)\right\}^{\left(\mathrm{1}\right)} \:={lim}_{{z}\rightarrow\mathrm{0}} \left\{−\mathrm{3}{sin}\left(\mathrm{3}{z}\right)\right\}\:=\mathrm{0}\:. \\ $$
