Question Number 150590 by liberty last updated on 13/Aug/21
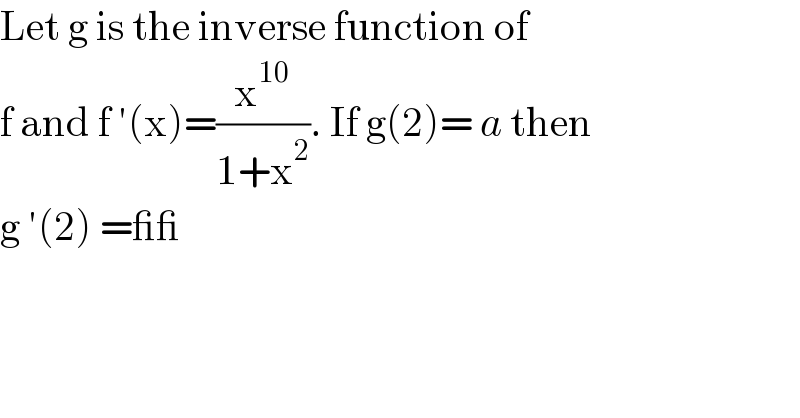
$$\mathrm{Let}\:\mathrm{g}\:\mathrm{is}\:\mathrm{the}\:\mathrm{inverse}\:\mathrm{function}\:\mathrm{of} \\ $$$$\mathrm{f}\:\mathrm{and}\:\mathrm{f}\:'\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{10}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }.\:\mathrm{If}\:\mathrm{g}\left(\mathrm{2}\right)=\:{a}\:\mathrm{then} \\ $$$$\mathrm{g}\:'\left(\mathrm{2}\right)\:=\_\_\: \\ $$
Answered by Olaf_Thorendsen last updated on 13/Aug/21
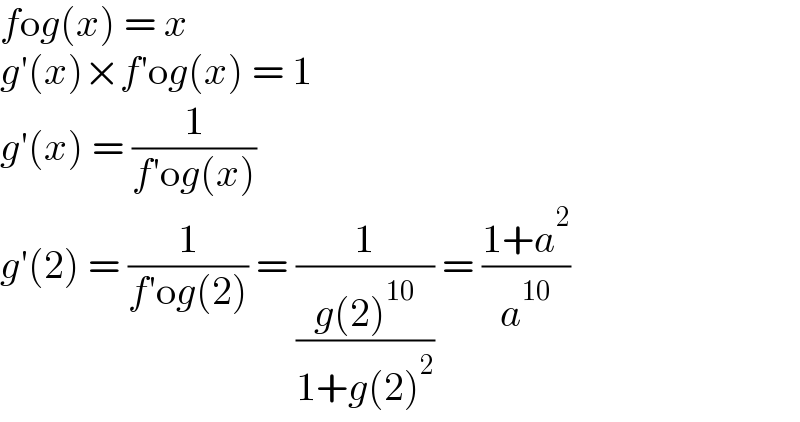
$${f}\mathrm{o}{g}\left({x}\right)\:=\:{x} \\ $$$${g}'\left({x}\right)×{f}'\mathrm{o}{g}\left({x}\right)\:=\:\mathrm{1} \\ $$$${g}'\left({x}\right)\:=\:\frac{\mathrm{1}}{{f}'\mathrm{o}{g}\left({x}\right)} \\ $$$${g}'\left(\mathrm{2}\right)\:=\:\frac{\mathrm{1}}{{f}'\mathrm{o}{g}\left(\mathrm{2}\right)}\:=\:\frac{\mathrm{1}}{\frac{{g}\left(\mathrm{2}\right)^{\mathrm{10}} }{\mathrm{1}+{g}\left(\mathrm{2}\right)^{\mathrm{2}} }}\:=\:\frac{\mathrm{1}+{a}^{\mathrm{2}} }{{a}^{\mathrm{10}} } \\ $$
