Menu Close

Let-g-R-R-be-given-by-g-x-3-4x-Prove-by-induction-that-for-all-positive-integers-n-g-n-x-4-n-1-4-n-x-If-for-every-positive-integer-k-we-inteprete-g-k-as-the-inverse-of-the-fu

Tinku Tara 0 Comments
Pin




Question Number 145641 by physicstutes last updated on 06/Jul/21
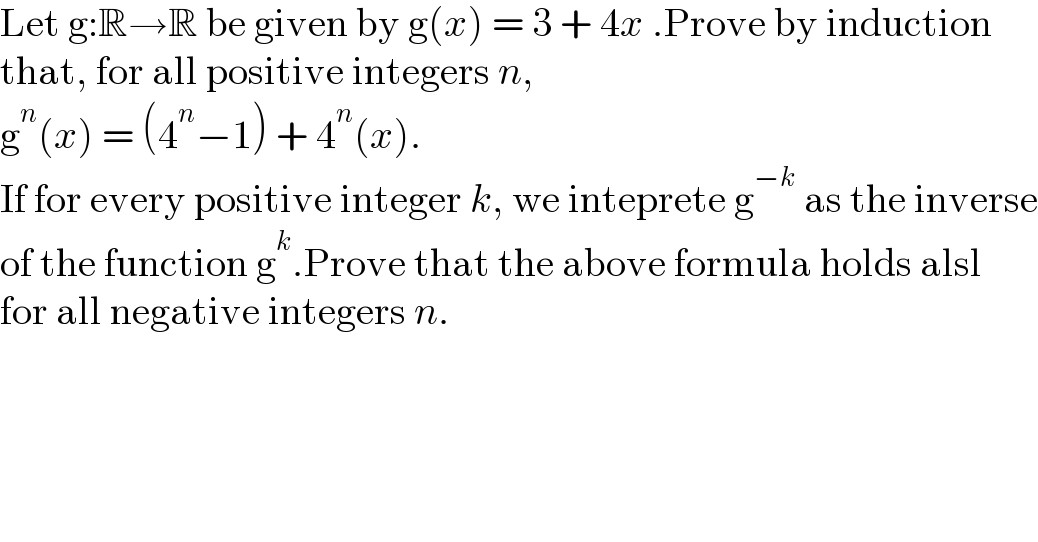
Let g:R→R be given by g(x) = 3 + 4x .Prove by induction that, for all positive integers n, g^n (x) = (4^n −1) + 4^n (x). If for every positive integer k, we inteprete g^(−k) as the inverse of the function g^k .Prove that the above formula holds alsl for all negative integers n.
$$\mathrm{Let}\:\mathrm{g}:\mathbb{R}\rightarrow\mathbb{R}\:\mathrm{be}\:\mathrm{given}\:\mathrm{by}\:\mathrm{g}\left({x}\right)\:=\:\mathrm{3}\:+\:\mathrm{4}{x}\:.\mathrm{Prove}\:\mathrm{by}\:\mathrm{induction} \\ $$$$\mathrm{that},\:\mathrm{for}\:\mathrm{all}\:\mathrm{positive}\:\mathrm{integers}\:{n},\: \\ $$$$\mathrm{g}^{{n}} \left({x}\right)\:=\:\left(\mathrm{4}^{{n}} −\mathrm{1}\right)\:+\:\mathrm{4}^{{n}} \left({x}\right). \\ $$$$\mathrm{If}\:\mathrm{for}\:\mathrm{every}\:\mathrm{positive}\:\mathrm{integer}\:{k},\:\mathrm{we}\:\mathrm{inteprete}\:\mathrm{g}^{−{k}} \:\mathrm{as}\:\mathrm{the}\:\mathrm{inverse} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:\mathrm{g}^{{k}} .\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{above}\:\mathrm{formula}\:\mathrm{holds}\:\mathrm{alsl} \\ $$$$\mathrm{for}\:\mathrm{all}\:\mathrm{negative}\:\mathrm{integers}\:{n}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *