Menu Close

let-g-x-2-cos-pix-developp-g-at-fourier-serie-

Tinku Tara 0 Comments
Pin




Question Number 98430 by mathmax by abdo last updated on 13/Jun/20
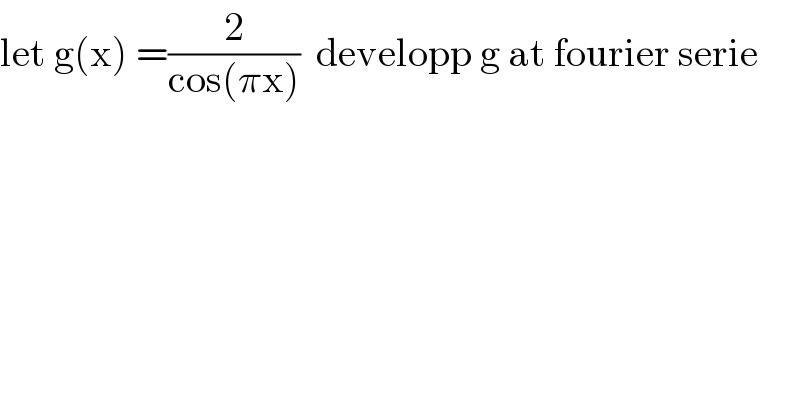
let g(x) =(2/(cos(πx))) developp g at fourier serie
$$\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{2}}{\mathrm{cos}\left(\pi\mathrm{x}\right)}\:\:\mathrm{developp}\:\mathrm{g}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$
Answered by abdomathmax last updated on 13/Jun/20
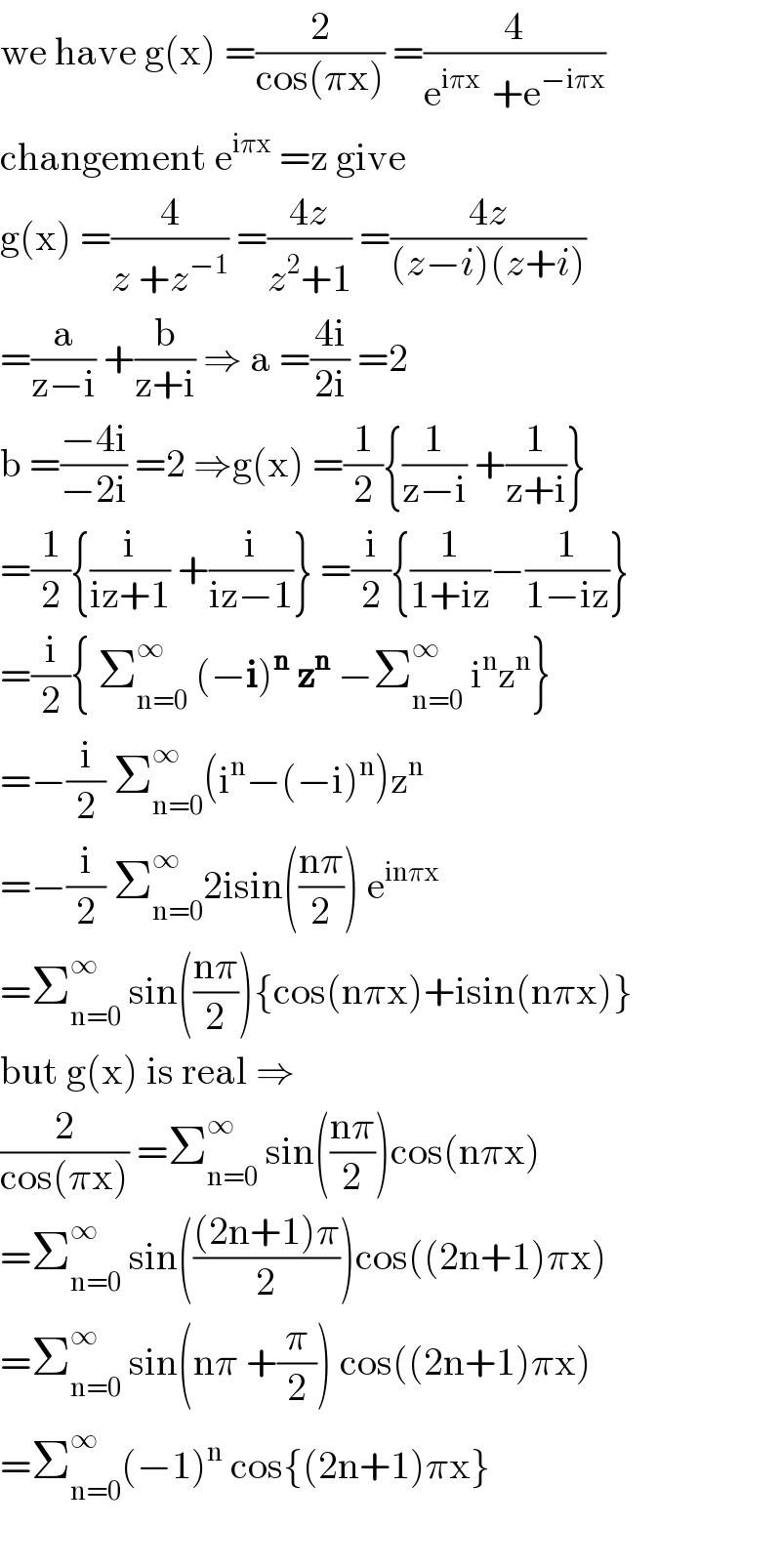
we have g(x) =(2/(cos(πx))) =(4/(e^(iπx ) +e^(−iπx) )) changement e^(iπx) =z give g(x) =(4/(z +z^(−1) )) =((4z)/(z^2 +1)) =((4z)/((z−i)(z+i))) =(a/(z−i)) +(b/(z+i)) ⇒ a =((4i)/(2i)) =2 b =((−4i)/(−2i)) =2 ⇒g(x) =(1/2){(1/(z−i)) +(1/(z+i))} =(1/2){(i/(iz+1)) +(i/(iz−1))} =(i/2){(1/(1+iz))−(1/(1−iz))} =(i/2){ Σ_(n=0) ^∞ (−i)^n z^n −Σ_(n=0) ^∞ i^n z^n } =−(i/2) Σ_(n=0) ^∞ (i^n −(−i)^n )z^n =−(i/2) Σ_(n=0) ^∞ 2isin(((nπ)/2)) e^(inπx) =Σ_(n=0) ^∞ sin(((nπ)/2)){cos(nπx)+isin(nπx)} but g(x) is real ⇒ (2/(cos(πx))) =Σ_(n=0) ^∞ sin(((nπ)/2))cos(nπx) =Σ_(n=0) ^∞ sin((((2n+1)π)/2))cos((2n+1)πx) =Σ_(n=0) ^∞ sin(nπ +(π/2)) cos((2n+1)πx) =Σ_(n=0) ^∞ (−1)^n cos{(2n+1)πx}
$$\mathrm{we}\:\mathrm{have}\:\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{2}}{\mathrm{cos}\left(\pi\mathrm{x}\right)}\:=\frac{\mathrm{4}}{\mathrm{e}^{\mathrm{i}\pi\mathrm{x}\:} \:+\mathrm{e}^{−\mathrm{i}\pi\mathrm{x}} } \\ $$$$\mathrm{changement}\:\mathrm{e}^{\mathrm{i}\pi\mathrm{x}} \:=\mathrm{z}\:\mathrm{give} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{4}}{{z}\:+{z}^{−\mathrm{1}} }\:=\frac{\mathrm{4}{z}}{{z}^{\mathrm{2}} +\mathrm{1}}\:=\frac{\mathrm{4}{z}}{\left({z}−{i}\right)\left({z}+{i}\right)} \\ $$$$=\frac{\mathrm{a}}{\mathrm{z}−\mathrm{i}}\:+\frac{\mathrm{b}}{\mathrm{z}+\mathrm{i}}\:\Rightarrow\:\mathrm{a}\:=\frac{\mathrm{4i}}{\mathrm{2i}}\:=\mathrm{2} \\ $$$$\mathrm{b}\:=\frac{−\mathrm{4i}}{−\mathrm{2i}}\:=\mathrm{2}\:\Rightarrow\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{z}−\mathrm{i}}\:+\frac{\mathrm{1}}{\mathrm{z}+\mathrm{i}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{i}}{\mathrm{iz}+\mathrm{1}}\:+\frac{\mathrm{i}}{\mathrm{iz}−\mathrm{1}}\right\}\:=\frac{\mathrm{i}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{iz}}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{iz}}\right\} \\ $$$$=\frac{\mathrm{i}}{\mathrm{2}}\left\{\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\boldsymbol{\mathrm{i}}\right)^{\boldsymbol{\mathrm{n}}} \:\boldsymbol{\mathrm{z}}^{\boldsymbol{\mathrm{n}}} \:−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{i}^{\mathrm{n}} \mathrm{z}^{\mathrm{n}} \right\} \\ $$$$=−\frac{\mathrm{i}}{\mathrm{2}}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(\mathrm{i}^{\mathrm{n}} −\left(−\mathrm{i}\right)^{\mathrm{n}} \right)\mathrm{z}^{\mathrm{n}} \\ $$$$=−\frac{\mathrm{i}}{\mathrm{2}}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \mathrm{2isin}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\:\mathrm{e}^{\mathrm{in}\pi\mathrm{x}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{sin}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\left\{\mathrm{cos}\left(\mathrm{n}\pi\mathrm{x}\right)+\mathrm{isin}\left(\mathrm{n}\pi\mathrm{x}\right)\right\} \\ $$$$\mathrm{but}\:\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{real}\:\Rightarrow \\ $$$$\frac{\mathrm{2}}{\mathrm{cos}\left(\pi\mathrm{x}\right)}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{sin}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\mathrm{cos}\left(\mathrm{n}\pi\mathrm{x}\right) \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{sin}\left(\frac{\left(\mathrm{2n}+\mathrm{1}\right)\pi}{\mathrm{2}}\right)\mathrm{cos}\left(\left(\mathrm{2n}+\mathrm{1}\right)\pi\mathrm{x}\right) \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{sin}\left(\mathrm{n}\pi\:+\frac{\pi}{\mathrm{2}}\right)\:\mathrm{cos}\left(\left(\mathrm{2n}+\mathrm{1}\right)\pi\mathrm{x}\right) \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{cos}\left\{\left(\mathrm{2n}+\mathrm{1}\right)\pi\mathrm{x}\right\} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *