Question Number 96656 by mathmax by abdo last updated on 03/Jun/20
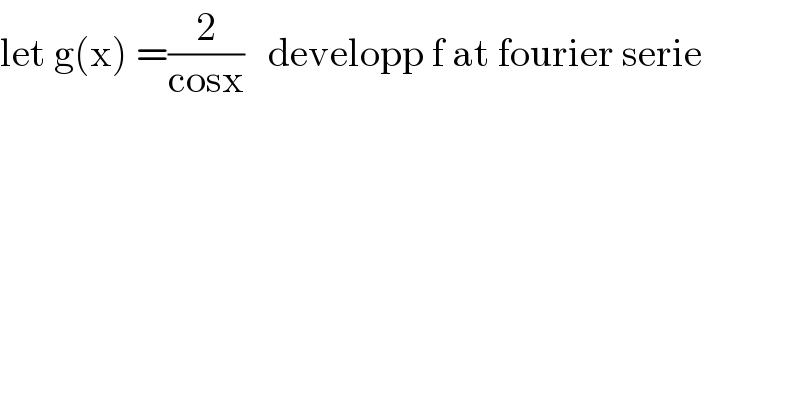
$$\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{2}}{\mathrm{cosx}}\:\:\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$
Answered by mathmax by abdo last updated on 04/Jun/20
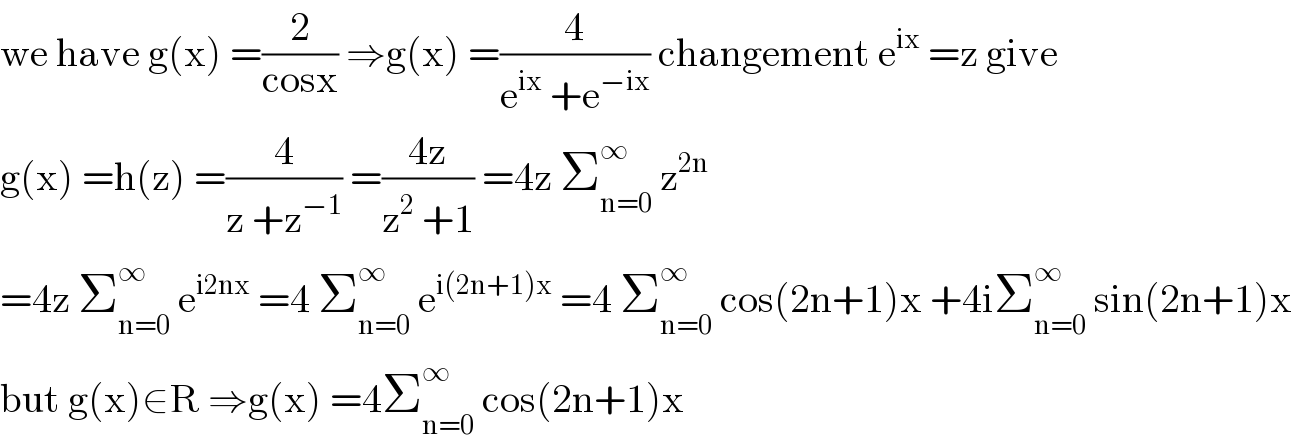
$$\mathrm{we}\:\mathrm{have}\:\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{2}}{\mathrm{cosx}}\:\Rightarrow\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{4}}{\mathrm{e}^{\mathrm{ix}} \:+\mathrm{e}^{−\mathrm{ix}} }\:\mathrm{changement}\:\mathrm{e}^{\mathrm{ix}} \:=\mathrm{z}\:\mathrm{give} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\:=\mathrm{h}\left(\mathrm{z}\right)\:=\frac{\mathrm{4}}{\mathrm{z}\:+\mathrm{z}^{−\mathrm{1}} }\:=\frac{\mathrm{4z}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\:=\mathrm{4z}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{z}^{\mathrm{2n}} \\ $$$$=\mathrm{4z}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{\mathrm{i2nx}} \:=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}} \:=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}\:+\mathrm{4i}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{sin}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x} \\ $$$$\mathrm{but}\:\mathrm{g}\left(\mathrm{x}\right)\in\mathrm{R}\:\Rightarrow\mathrm{g}\left(\mathrm{x}\right)\:=\mathrm{4}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}\: \\ $$
Commented by 1549442205 last updated on 04/Jun/20
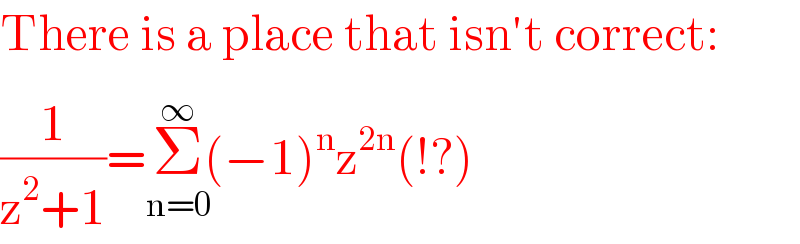
$$\mathrm{There}\:\mathrm{is}\:\mathrm{a}\:\mathrm{place}\:\mathrm{that}\:\mathrm{isn}'\mathrm{t}\:\mathrm{correct}: \\ $$$$\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} +\mathrm{1}}=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\Sigma}}\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{z}^{\mathrm{2n}} \left(!?\right) \\ $$
Commented by Rio Michael last updated on 04/Jun/20
$$\mathrm{i}\:\mathrm{have}\:\mathrm{to}\:\mathrm{study}\:\mathrm{in}\:\mathrm{dept}\:\mathrm{this}\:\mathrm{fourier}\:\mathrm{series}. \\ $$$$\mathrm{sorry}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{much}\:\mathrm{about}\:\mathrm{it}. \\ $$
Commented by abdomathmax last updated on 04/Jun/20
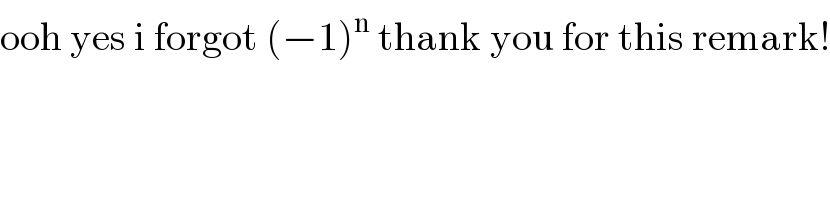
$$\mathrm{ooh}\:\mathrm{yes}\:\mathrm{i}\:\mathrm{forgot}\:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{this}\:\mathrm{remark}! \\ $$
Commented by abdomathmax last updated on 04/Jun/20
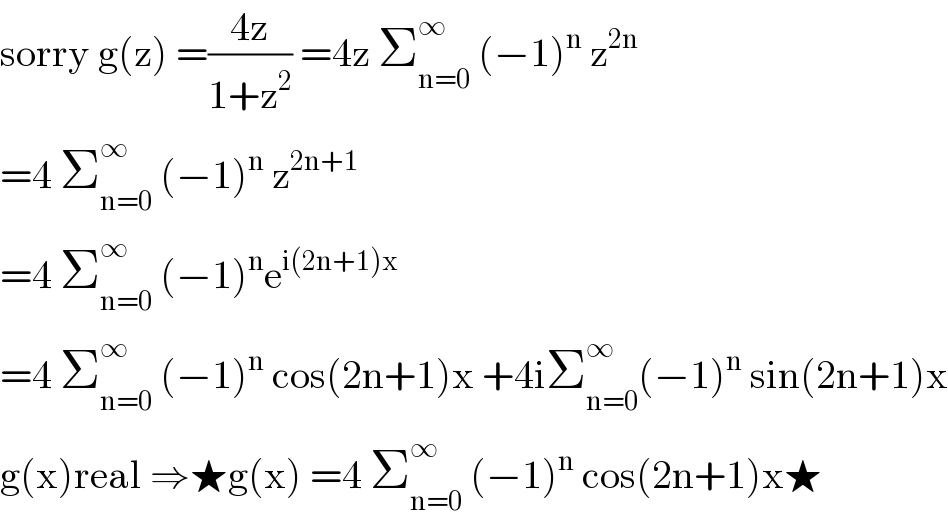
$$\mathrm{sorry}\:\mathrm{g}\left(\mathrm{z}\right)\:=\frac{\mathrm{4z}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\:=\mathrm{4z}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{z}^{\mathrm{2n}} \\ $$$$=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{z}^{\mathrm{2n}+\mathrm{1}} \\ $$$$=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{e}^{\mathrm{i}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}} \\ $$$$=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{cos}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}\:+\mathrm{4i}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{sin}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\mathrm{real}\:\Rightarrow\bigstar\mathrm{g}\left(\mathrm{x}\right)\:=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{cos}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}\bigstar \\ $$
