Menu Close

let-g-x-cosx-1-cos-2x-3-developp-f-at-fourier-serie-

Tinku Tara 0 Comments
Pin




Question Number 98944 by mathmax by abdo last updated on 17/Jun/20
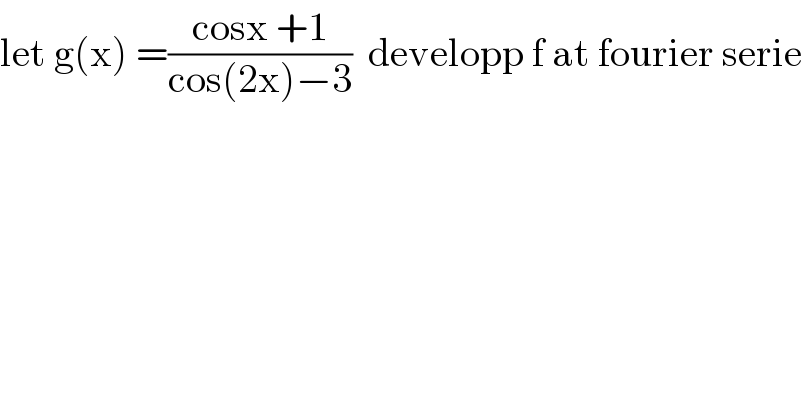
let g(x) =((cosx +1)/(cos(2x)−3)) developp f at fourier serie
$$\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{cosx}\:+\mathrm{1}}{\mathrm{cos}\left(\mathrm{2x}\right)−\mathrm{3}}\:\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$
Answered by mathmax by abdo last updated on 18/Jun/20
g(x) =((cosx+1)/(cos(2x)−3)) =((((e^(ix) +e^(−ix) )/2)+1)/(((e^(2ix) +e^(−i2x) )/2)−3)) =((e^(ix) +e^(−ix) +2)/(e^(i2x) +e^(−i2x) −6)) changement e^(ix) =z give g(x) =((z+z^(−1) +2)/(z^2 +z^(−2) −6)) =((z^3 +z +2z^2 )/(z^4 +1−6z^2 )) =((z^3 +2z^2 +z)/(z^4 −6z^2 +1)) =f(z) let decompose f z^4 −6z^2 +1 =0→u^2 −6u +1 =0 →Δ^′ =9−1 =8 ⇒ u_1 =3+2(√2) and u_2 =3−2(√2) ⇒f(z) =((z^3 +2z^2 +z)/((z^2 −u_1 )(z^2 −u_2 ))) =(z^3 +2z^2 +z)((1/(z^2 −u_1 ))−(1/(z^2 −u_2 ))) =((z^3 +2z^2 +z)/(z^2 −u_1 ))−((z^3 +2z^2 +z)/(z^2 −u_2 )) =ϕ_1 (z)−ϕ_2 (z) ϕ_1 (z) =((z(z^2 −u_1 )+zu_1 +2z^2 +z)/(z^2 −u_1 )) =z +((2z^2 +(1+u_1 )z)/(z^2 −u_1 )) =z +((2(z^2 −u_1 )+2u_1 +(1+u_1 )z)/(z^2 −u_1 )) =z+2 +(((1+u_1 )z +2u_1 )/(z^2 −u_1 )) ϕ_2 (z) =z+2 +(((1+u_2 )z +2u_2 )/(z^2 −u_2 )) ⇒f(z) =(((1+u_1 )z +2u_1 )/(z^2 −u_1 ))−(((1+u_2 )z +2u_2 )/(z^2 −u_2 )) f(z) =(((1+u_2 )z +2u_2 )/(u_2 −z^2 ))−(((1+u_1 )z +2u_1 )/(u_1 −z^2 )) =(1/u_2 )×(((1+u_2 )z+2u_2 )/(1−((z/( (√u_2 ))))^2 )) −(1/u_1 )×(((1+u_1 )z+2u_1 )/(1−((z/( (√u_1 ))))^2 )) so if ∣z∣ <inf((√u_1 ),(√u_2 )) weget f(z) =(1/u_2 ){(1+u_2 )z +2u_2 }Σ_(n=0) ^∞ (z^(2n) /u_2 ^n ) −(1/u_1 ){ (1+u_1 )z +2u_1 }Σ_(n=0) ^∞ (z^(2n) /u_1 ^n ) =(1/(3−2(√2))){(4−2(√2))z +6−4(√2)}Σ_(n=0) ^∞ (e^(2inx) /((3−2(√2))^n )) −(1/(3+2(√2))){ (4+2(√2))+6+4(√2)}Σ_(n=0) ^∞ (e^(2inx) /((3+2(√2))^n ))
$$\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{cosx}+\mathrm{1}}{\mathrm{cos}\left(\mathrm{2x}\right)−\mathrm{3}}\:=\frac{\frac{\mathrm{e}^{\mathrm{ix}} \:+\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2}}+\mathrm{1}}{\frac{\mathrm{e}^{\mathrm{2ix}} +\mathrm{e}^{−\mathrm{i2x}} }{\mathrm{2}}−\mathrm{3}}\:=\frac{\mathrm{e}^{\mathrm{ix}} +\mathrm{e}^{−\mathrm{ix}} \:+\mathrm{2}}{\mathrm{e}^{\mathrm{i2x}} +\mathrm{e}^{−\mathrm{i2x}} −\mathrm{6}} \\ $$$$\mathrm{changement}\:\mathrm{e}^{\mathrm{ix}} \:=\mathrm{z}\:\mathrm{give}\:\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{z}+\mathrm{z}^{−\mathrm{1}} \:+\mathrm{2}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{z}^{−\mathrm{2}} \:−\mathrm{6}}\:=\frac{\mathrm{z}^{\mathrm{3}} \:+\mathrm{z}\:+\mathrm{2z}^{\mathrm{2}} }{\mathrm{z}^{\mathrm{4}} \:+\mathrm{1}−\mathrm{6z}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{z}^{\mathrm{3}} \:+\mathrm{2z}^{\mathrm{2}} \:+\mathrm{z}}{\mathrm{z}^{\mathrm{4}} −\mathrm{6z}^{\mathrm{2}} \:+\mathrm{1}}\:=\mathrm{f}\left(\mathrm{z}\right)\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{f} \\ $$$$\mathrm{z}^{\mathrm{4}} −\mathrm{6z}^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{0}\rightarrow\mathrm{u}^{\mathrm{2}} −\mathrm{6u}\:+\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{9}−\mathrm{1}\:=\mathrm{8}\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{1}} =\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{and}\:\mathrm{u}_{\mathrm{2}} =\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:\Rightarrow\mathrm{f}\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{3}} \:+\mathrm{2z}^{\mathrm{2}} +\mathrm{z}}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} \right)\left(\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} \right)} \\ $$$$=\left(\mathrm{z}^{\mathrm{3}} \:+\mathrm{2z}^{\mathrm{2}} \:+\mathrm{z}\right)\left(\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\right)\:=\frac{\mathrm{z}^{\mathrm{3}} \:+\mathrm{2z}^{\mathrm{2}} \:+\mathrm{z}}{\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }−\frac{\mathrm{z}^{\mathrm{3}} \:+\mathrm{2z}^{\mathrm{2}} \:+\mathrm{z}}{\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\:=\varphi_{\mathrm{1}} \left(\mathrm{z}\right)−\varphi_{\mathrm{2}} \left(\mathrm{z}\right) \\ $$$$\varphi_{\mathrm{1}} \left(\mathrm{z}\right)\:=\frac{\mathrm{z}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} \right)+\mathrm{zu}_{\mathrm{1}} +\mathrm{2z}^{\mathrm{2}} \:+\mathrm{z}}{\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }\:=\mathrm{z}\:\:+\frac{\mathrm{2z}^{\mathrm{2}} \:+\left(\mathrm{1}+\mathrm{u}_{\mathrm{1}} \right)\mathrm{z}}{\mathrm{z}^{\mathrm{2}} \:−\mathrm{u}_{\mathrm{1}} } \\ $$$$=\mathrm{z}\:+\frac{\mathrm{2}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} \right)+\mathrm{2u}_{\mathrm{1}} +\left(\mathrm{1}+\mathrm{u}_{\mathrm{1}} \right)\mathrm{z}}{\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }\:=\mathrm{z}+\mathrm{2}\:+\frac{\left(\mathrm{1}+\mathrm{u}_{\mathrm{1}} \right)\mathrm{z}\:+\mathrm{2u}_{\mathrm{1}} }{\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} } \\ $$$$\varphi_{\mathrm{2}} \left(\mathrm{z}\right)\:=\mathrm{z}+\mathrm{2}\:+\frac{\left(\mathrm{1}+\mathrm{u}_{\mathrm{2}} \right)\mathrm{z}\:+\mathrm{2u}_{\mathrm{2}} }{\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\:\Rightarrow\mathrm{f}\left(\mathrm{z}\right)\:=\frac{\left(\mathrm{1}+\mathrm{u}_{\mathrm{1}} \right)\mathrm{z}\:+\mathrm{2u}_{\mathrm{1}} }{\mathrm{z}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }−\frac{\left(\mathrm{1}+\mathrm{u}_{\mathrm{2}} \right)\mathrm{z}\:+\mathrm{2u}_{\mathrm{2}} }{\mathrm{z}^{\mathrm{2}} \:−\mathrm{u}_{\mathrm{2}} } \\ $$$$\mathrm{f}\left(\mathrm{z}\right)\:=\frac{\left(\mathrm{1}+\mathrm{u}_{\mathrm{2}} \right)\mathrm{z}\:+\mathrm{2u}_{\mathrm{2}} }{\mathrm{u}_{\mathrm{2}} −\mathrm{z}^{\mathrm{2}} }−\frac{\left(\mathrm{1}+\mathrm{u}_{\mathrm{1}} \right)\mathrm{z}\:+\mathrm{2u}_{\mathrm{1}} }{\mathrm{u}_{\mathrm{1}} −\mathrm{z}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{u}_{\mathrm{2}} }×\frac{\left(\mathrm{1}+\mathrm{u}_{\mathrm{2}} \right)\mathrm{z}+\mathrm{2u}_{\mathrm{2}} }{\mathrm{1}−\left(\frac{\mathrm{z}}{\:\sqrt{\mathrm{u}_{\mathrm{2}} }}\right)^{\mathrm{2}} } \\ $$$$−\frac{\mathrm{1}}{\mathrm{u}_{\mathrm{1}} }×\frac{\left(\mathrm{1}+\mathrm{u}_{\mathrm{1}} \right)\mathrm{z}+\mathrm{2u}_{\mathrm{1}} }{\mathrm{1}−\left(\frac{\mathrm{z}}{\:\sqrt{\mathrm{u}_{\mathrm{1}} }}\right)^{\mathrm{2}} }\:\mathrm{so}\:\mathrm{if}\:\mid\mathrm{z}\mid\:<\mathrm{inf}\left(\sqrt{\mathrm{u}_{\mathrm{1}} },\sqrt{\mathrm{u}_{\mathrm{2}} }\right)\:\mathrm{weget}\: \\ $$$$\mathrm{f}\left(\mathrm{z}\right)\:=\frac{\mathrm{1}}{\mathrm{u}_{\mathrm{2}} }\left\{\left(\mathrm{1}+\mathrm{u}_{\mathrm{2}} \right)\mathrm{z}\:+\mathrm{2u}_{\mathrm{2}} \right\}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{z}^{\mathrm{2n}} }{\mathrm{u}_{\mathrm{2}} ^{\mathrm{n}} }\:−\frac{\mathrm{1}}{\mathrm{u}_{\mathrm{1}} }\left\{\:\left(\mathrm{1}+\mathrm{u}_{\mathrm{1}} \right)\mathrm{z}\:+\mathrm{2u}_{\mathrm{1}} \right\}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{z}^{\mathrm{2n}} }{\mathrm{u}_{\mathrm{1}} ^{\mathrm{n}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}\left\{\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)\mathrm{z}\:+\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}}\right\}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{2inx}} }{\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} } \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}\right)+\mathrm{6}+\mathrm{4}\sqrt{\mathrm{2}}\right\}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{2inx}} }{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *