Menu Close

let-g-x-e-2x-arctan-x-3-developp-g-at-integr-serie-

Tinku Tara 0 Comments
Pin




Question Number 39892 by math khazana by abdo last updated on 13/Jul/18
let g(x)= e^(−2x) arctan(x+3) developp g at integr serie .
$${let}\:{g}\left({x}\right)=\:{e}^{−\mathrm{2}{x}} \:{arctan}\left({x}+\mathrm{3}\right) \\ $$$${developp}\:{g}\:{at}\:{integr}\:{serie}\:\:. \\ $$
Commented by math khazana by abdo last updated on 13/Jul/18
we have g^((n)) (x) = Σ_(k=0) ^n (arctan(x+3))^((k)) (e^(−2x)) )^((n−k)) but arctan(x+3)^((1)) = (1/((1+(x+3)^2 )) ⇒ (arctan(x+3)}^((n)) = { (1/((x+3)^2 +1))}^((n−1)) let w(x)= (1/((x+3)^2 +1)) w(x)= (1/((x+3+i)(x+3−i))) = (a/(x+3+i)) +(b/(x+3−i)) a =lim_(x→−3−i) (x+3+i)w(z) = (1/(−3−i+3−i)) =−(1/(2i)) b=lim_(x→−3+i) (x+3−i)w(z)= (1/(−3+i+3+i)) =(1/(2i)) w(x)=(1/(2i)){ (1/(x+3−i)) −(1/(x+3+i))} ⇒(arctan(x+3))^((k)) =(1/(2i)){ ( (1/(x+3−i)))^((k−1))) −((1/(x+3+i)))^((k−1)) } = (1/(2i)) (((−1)^(k−1) (k−1)!)/((x+3−i)^k )) −(1/(2i))(((−1)^(k−1) (k−1)!)/((x+3+i)^k )) ⇒ g^((n)) (x) =Σ_(k=0) ^n (((−1)^(k−1) (k−1)!)/(2i)){ (1/((x+3−i)^k )) −(1/((x+3+i)^k ))}(−2)^(n−k) e^(−2x)
$${we}\:{have}\:{g}^{\left({n}\right)} \left({x}\right)\:=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\left({arctan}\left({x}+\mathrm{3}\right)\right)^{\left({k}\right)} \left({e}^{\left.−\mathrm{2}{x}\right)} \right)^{\left({n}−{k}\right)} \\ $$$${but}\:{arctan}\left({x}+\mathrm{3}\right)^{\left(\mathrm{1}\right)} =\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+\left({x}+\mathrm{3}\right)^{\mathrm{2}} \right.} \\ $$$$\Rightarrow\:\left({arctan}\left({x}+\mathrm{3}\right)\right\}^{\left({n}\right)} \:=\:\left\{\:\frac{\mathrm{1}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{1}}\right\}^{\left({n}−\mathrm{1}\right)} \\ $$$${let}\:{w}\left({x}\right)=\:\frac{\mathrm{1}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$${w}\left({x}\right)=\:\frac{\mathrm{1}}{\left({x}+\mathrm{3}+{i}\right)\left({x}+\mathrm{3}−{i}\right)}\:=\:\frac{{a}}{{x}+\mathrm{3}+{i}}\:+\frac{{b}}{{x}+\mathrm{3}−\mathrm{i}} \\ $$$$\mathrm{a}\:=\mathrm{lim}_{\mathrm{x}\rightarrow−\mathrm{3}−{i}} \left({x}+\mathrm{3}+{i}\right){w}\left({z}\right)\:=\:\frac{\mathrm{1}}{−\mathrm{3}−{i}+\mathrm{3}−{i}}\:=−\frac{\mathrm{1}}{\mathrm{2}{i}} \\ $$$${b}={lim}_{{x}\rightarrow−\mathrm{3}+{i}} \left({x}+\mathrm{3}−{i}\right){w}\left({z}\right)=\:\frac{\mathrm{1}}{−\mathrm{3}+{i}+\mathrm{3}+{i}}\:=\frac{\mathrm{1}}{\mathrm{2}{i}} \\ $$$${w}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\:\:\:\frac{\mathrm{1}}{{x}+\mathrm{3}−{i}}\:−\frac{\mathrm{1}}{{x}+\mathrm{3}+{i}}\right\} \\ $$$$\Rightarrow\left({arctan}\left({x}+\mathrm{3}\right)\right)^{\left({k}\right)} \:=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\:\left(\:\frac{\mathrm{1}}{{x}+\mathrm{3}−{i}}\right)^{\left.\left({k}−\mathrm{1}\right)\right)} \:−\left(\frac{\mathrm{1}}{{x}+\mathrm{3}+{i}}\right)^{\left({k}−\mathrm{1}\right)} \right\} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}{i}}\:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\left({x}+\mathrm{3}−{i}\right)^{{k}} }\:−\frac{\mathrm{1}}{\mathrm{2}{i}}\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\left({x}+\mathrm{3}+{i}\right)^{{k}} }\:\Rightarrow \\ $$$${g}^{\left({n}\right)} \left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\:\frac{\mathrm{1}}{\left({x}+\mathrm{3}−{i}\right)^{{k}} }\:−\frac{\mathrm{1}}{\left({x}+\mathrm{3}+{i}\right)^{{k}} }\right\}\left(−\mathrm{2}\right)^{{n}−{k}} \:{e}^{−\mathrm{2}{x}} \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 13/Jul/18
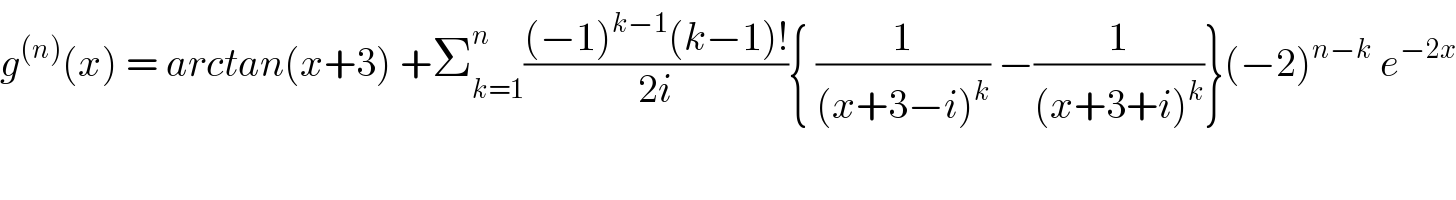
g^((n)) (x) = arctan(x+3) +Σ_(k=1) ^n (((−1)^(k−1) (k−1)!)/(2i)){ (1/((x+3−i)^k )) −(1/((x+3+i)^k ))}(−2)^(n−k) e^(−2x)
$${g}^{\left({n}\right)} \left({x}\right)\:=\:{arctan}\left({x}+\mathrm{3}\right)\:+\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\:\frac{\mathrm{1}}{\left({x}+\mathrm{3}−{i}\right)^{{k}} }\:−\frac{\mathrm{1}}{\left({x}+\mathrm{3}+{i}\right)^{{k}} }\right\}\left(−\mathrm{2}\right)^{{n}−{k}} \:{e}^{−\mathrm{2}{x}} \\ $$
Commented by math khazana by abdo last updated on 13/Jul/18
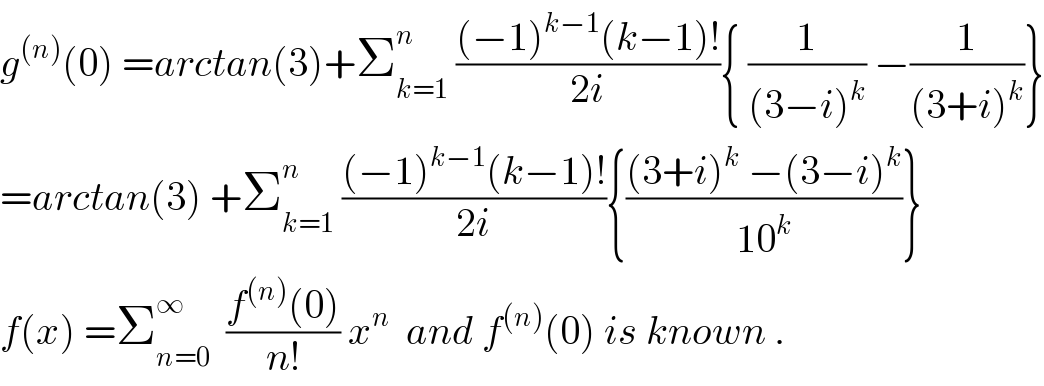
g^((n)) (0) =arctan(3)+Σ_(k=1) ^n (((−1)^(k−1) (k−1)!)/(2i)){ (1/((3−i)^k )) −(1/((3+i)^k ))} =arctan(3) +Σ_(k=1) ^n (((−1)^(k−1) (k−1)!)/(2i)){(((3+i)^k −(3−i)^k )/(10^k ))} f(x) =Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n and f^((n)) (0) is known .
$${g}^{\left({n}\right)} \left(\mathrm{0}\right)\:={arctan}\left(\mathrm{3}\right)+\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\:\frac{\mathrm{1}}{\left(\mathrm{3}−{i}\right)^{{k}} }\:−\frac{\mathrm{1}}{\left(\mathrm{3}+{i}\right)^{{k}} }\right\} \\ $$$$={arctan}\left(\mathrm{3}\right)\:+\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\frac{\left(\mathrm{3}+{i}\right)^{{k}} \:−\left(\mathrm{3}−{i}\right)^{{k}} }{\mathrm{10}^{{k}} }\right\} \\ $$$${f}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \:\:{and}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right)\:{is}\:{known}\:. \\ $$
Commented by maxmathsup by imad last updated on 13/Jul/18
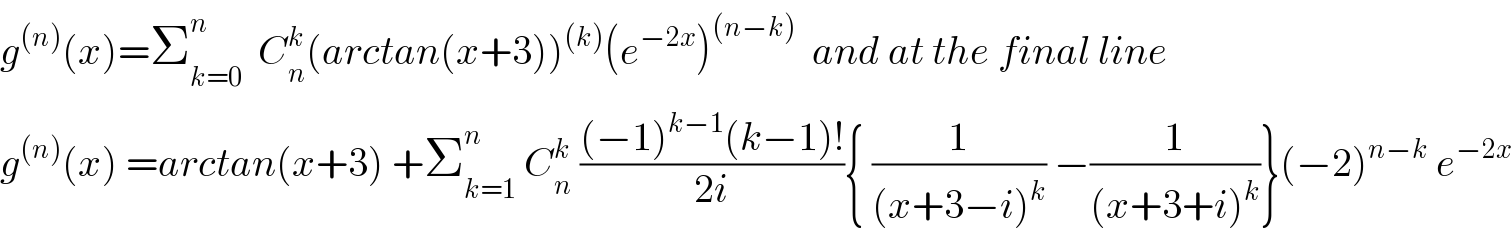
g^((n)) (x)=Σ_(k=0) ^n C_n ^k (arctan(x+3))^((k)) (e^(−2x) )^((n−k)) and at the final line g^((n)) (x) =arctan(x+3) +Σ_(k=1) ^n C_n ^k (((−1)^(k−1) (k−1)!)/(2i)){ (1/((x+3−i)^k )) −(1/((x+3+i)^k ))}(−2)^(n−k) e^(−2x)
$${g}^{\left({n}\right)} \left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \left({arctan}\left({x}+\mathrm{3}\right)\right)^{\left({k}\right)} \left({e}^{−\mathrm{2}{x}} \right)^{\left({n}−{k}\right)} \:\:{and}\:{at}\:{the}\:{final}\:{line} \\ $$$${g}^{\left({n}\right)} \left({x}\right)\:={arctan}\left({x}+\mathrm{3}\right)\:+\sum_{{k}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\:\frac{\mathrm{1}}{\left({x}+\mathrm{3}−{i}\right)^{{k}} }\:−\frac{\mathrm{1}}{\left({x}+\mathrm{3}+{i}\right)^{{k}} }\right\}\left(−\mathrm{2}\right)^{{n}−{k}} \:{e}^{−\mathrm{2}{x}} \\ $$
Commented by maxmathsup by imad last updated on 13/Jul/18
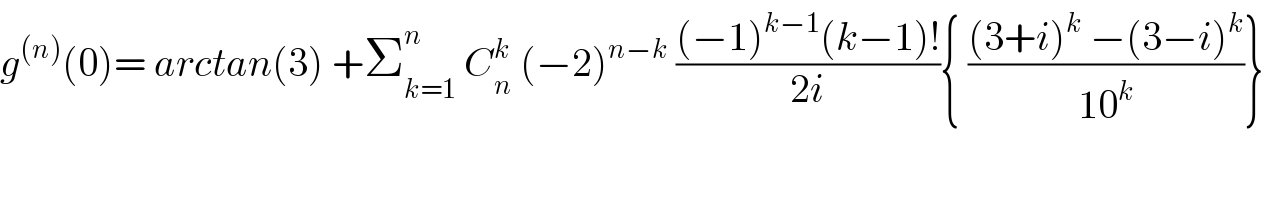
g^((n)) (0)= arctan(3) +Σ_(k=1) ^n C_n ^k (−2)^(n−k) (((−1)^(k−1) (k−1)!)/(2i)){ (((3+i)^k −(3−i)^k )/(10^k ))}
$${g}^{\left({n}\right)} \left(\mathrm{0}\right)=\:{arctan}\left(\mathrm{3}\right)\:+\sum_{{k}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left(−\mathrm{2}\right)^{{n}−{k}} \:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\:\frac{\left(\mathrm{3}+{i}\right)^{{k}} \:−\left(\mathrm{3}−{i}\right)^{{k}} }{\mathrm{10}^{{k}} }\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *