Question Number 30517 by abdo imad last updated on 22/Feb/18
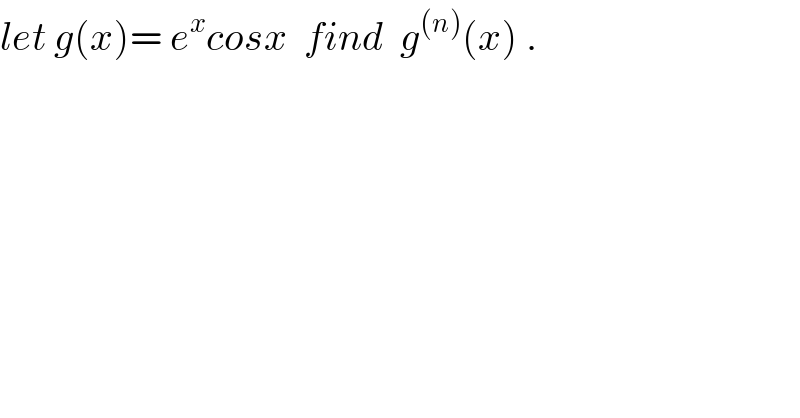
$${let}\:{g}\left({x}\right)=\:{e}^{{x}} {cosx}\:\:{find}\:\:{g}^{\left({n}\right)} \left({x}\right)\:. \\ $$
Commented by abdo imad last updated on 24/Feb/18
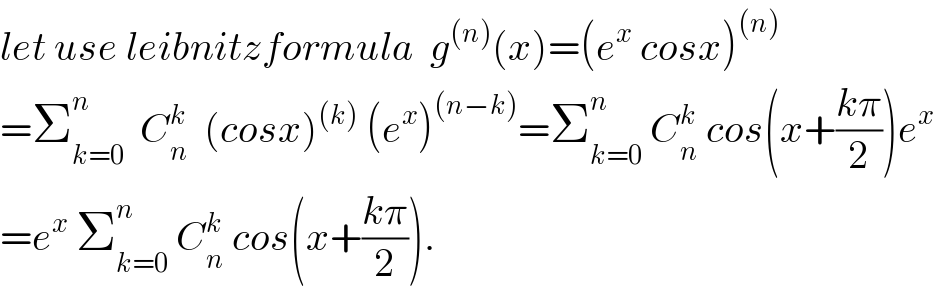
$${let}\:{use}\:{leibnitzformula}\:\:{g}^{\left({n}\right)} \left({x}\right)=\left({e}^{{x}} \:{cosx}\right)^{\left({n}\right)} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\:\left({cosx}\right)^{\left({k}\right)} \:\left({e}^{{x}} \right)^{\left({n}−{k}\right)} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}\left({x}+\frac{{k}\pi}{\mathrm{2}}\right){e}^{{x}} \\ $$$$={e}^{{x}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}\left({x}+\frac{{k}\pi}{\mathrm{2}}\right). \\ $$
