Question Number 37353 by math khazana by abdo last updated on 12/Jun/18
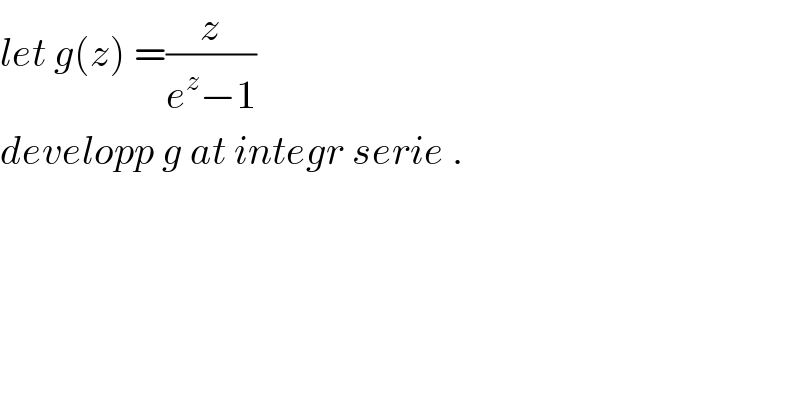
$${let}\:{g}\left({z}\right)\:=\frac{{z}}{{e}^{{z}} −\mathrm{1}} \\ $$$${developp}\:{g}\:{at}\:{integr}\:{serie}\:. \\ $$
Commented by prof Abdo imad last updated on 17/Jun/18
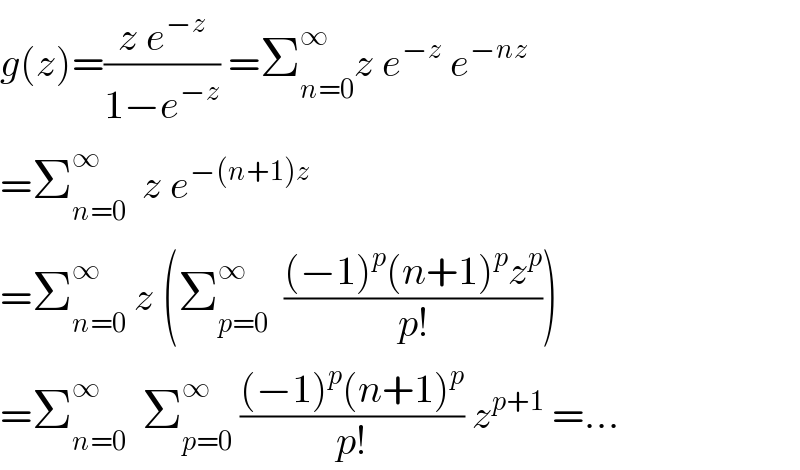
$${g}\left({z}\right)=\frac{{z}\:{e}^{−{z}} }{\mathrm{1}−{e}^{−{z}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} {z}\:{e}^{−{z}} \:{e}^{−{nz}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:{z}\:{e}^{−\left({n}+\mathrm{1}\right){z}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:{z}\:\left(\sum_{{p}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{p}} \left({n}+\mathrm{1}\right)^{{p}} {z}^{{p}} }{{p}!}\right) \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{p}} \left({n}+\mathrm{1}\right)^{{p}} }{{p}!}\:{z}^{{p}+\mathrm{1}} \:=… \\ $$
