Question Number 32737 by caravan msup abdo. last updated on 01/Apr/18
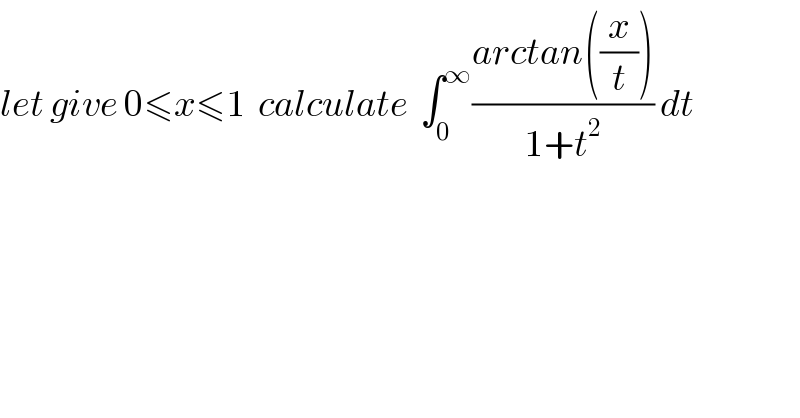
$${let}\:{give}\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:\:{calculate}\:\:\int_{\mathrm{0}} ^{\infty} \frac{{arctan}\left(\frac{{x}}{{t}}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$
Answered by hknkrc46 last updated on 09/Apr/18

$${t}={xcotu}\Rightarrow{dt}=−{xcsc}^{\mathrm{2}} {udu}\:\wedge\:\left({t}\rightarrow\mathrm{0}\Rightarrow{u}\rightarrow\frac{\pi}{\mathrm{2}}\:\wedge\:{t}\rightarrow\infty\Rightarrow{u}\rightarrow\mathrm{0}\right) \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \frac{−{uxcsc}^{\mathrm{2}} {u}}{\mathrm{1}+{x}^{\mathrm{2}} {cot}^{\mathrm{2}} {u}}{du}=\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \frac{−{ux}}{{sin}^{\mathrm{2}} {u}+{x}^{\mathrm{2}} {cos}^{\mathrm{2}} {u}}{du}=\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \frac{−{ux}}{\frac{\mathrm{1}−{cos}\mathrm{2}{u}+{x}^{\mathrm{2}} \left(\mathrm{1}+{cos}\mathrm{2}{u}\right)}{\mathrm{2}}}{du} \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \frac{−\mathrm{2}{ux}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right){cos}\mathrm{2}{u}+{x}^{\mathrm{2}} +\mathrm{1}}{du}=\frac{−\mathrm{2}{x}}{{x}^{\mathrm{2}} −\mathrm{1}}\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \frac{{u}}{{cos}\mathrm{2}{u}+\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}}{du} \\ $$$$=\frac{−\mathrm{2}{x}}{{x}^{\mathrm{2}} −\mathrm{1}}\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \frac{{u}}{\mathrm{2}{cos}^{\mathrm{2}} {u}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}}}{du}=\frac{−{x}}{{x}^{\mathrm{2}} −\mathrm{1}}\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \frac{{u}}{\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}+{cos}^{\mathrm{2}} {u}}{du} \\ $$$${I}\:{DO}\:{NOT}\:{KNOW}\:\::\left(\right. \\ $$
