Question Number 28428 by abdo imad last updated on 25/Jan/18
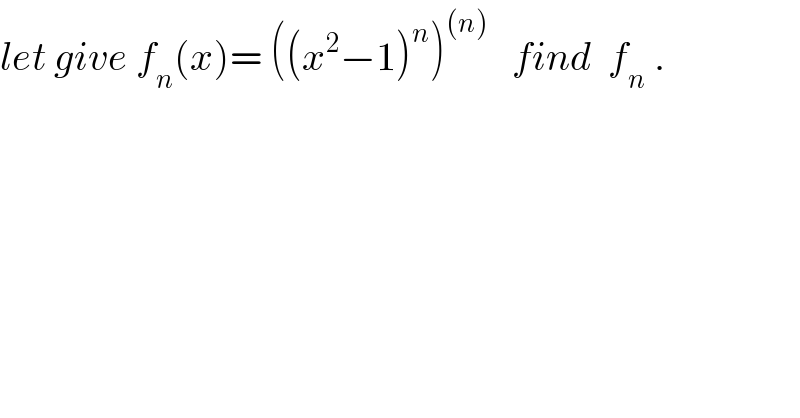
$${let}\:{give}\:{f}_{{n}} \left({x}\right)=\:\left(\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{{n}} \right)^{\left({n}\right)} \:\:\:{find}\:\:{f}_{{n}} \:. \\ $$
Commented by abdo imad last updated on 27/Jan/18
![we have f_n (x)= (p(x))^((n)) with p(x)=(x^2 −1)^n p(x)= Σ_(k=0) ^n C_n ^k x^(2k) (−1)^(n−k) =(−1)^n Σ_(k=0) ^n (−1)^k C_n ^k x^(2k) (p(x))^((n)) =(−1)^n Σ_(k=0) ^n (−1)^k C_n ^k (x^(2k) )^((n)) but if 2k<n (x^(2k) )^((n)) =0 so f_n (x)= (−1)^n Σ_(k=[((n−1)/2)] +1) ^n C_n ^k (x^(2k) )^((n)) .let find (x^p )^((n)) for p≥n wehave (x^p )^((1)) =p x^(p−1) ,(x^p )^((2)) =p(p−1)x^(p−2) so (x^p )^((n)) = p(p−1)....(p−n+1)x^(p−n) =((p(p−1)....(p−n+1)(p−n)!)/((p−n)!)) x^(p−n) =((p!)/((p−n)!)) x^(p−n) ⇒ (x^(2k) )^((n)) = (((2k)!)/((2k−n)!)) x^(2k−n) so f_n (x)= (−1)^n Σ_(k=[((n−1)/2)]+1) ^n C_n ^k (((2k)!)/((2k−n)!)) x^(2k−n) .](https://www.tinkutara.com/question/Q28572.png)
$$\:{we}\:{have}\:\:{f}_{{n}} \left({x}\right)=\:\left({p}\left({x}\right)\right)^{\left({n}\right)} \:\:{with}\:{p}\left({x}\right)=\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{{n}} \\ $$$${p}\left({x}\right)=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:{x}^{\mathrm{2}{k}} \left(−\mathrm{1}\right)^{{n}−{k}} =\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \left(−\mathrm{1}\right)^{{k}} \:{C}_{{n}} ^{{k}} \:{x}^{\mathrm{2}{k}} \\ $$$$\left({p}\left({x}\right)\right)^{\left({n}\right)} \:\:=\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \left(−\mathrm{1}\right)^{{k}} \:{C}_{{n}} ^{{k}} \:\left({x}^{\mathrm{2}{k}} \right)^{\left({n}\right)} \:\:{but}\:{if} \\ $$$$\mathrm{2}{k}<{n}\:\:\:\:\:\left({x}^{\mathrm{2}{k}} \right)^{\left({n}\right)} =\mathrm{0}\:\:\:\:{so}\: \\ $$$${f}_{{n}} \left({x}\right)=\:\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]\:+\mathrm{1}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\left({x}^{\mathrm{2}{k}} \right)^{\left({n}\right)} .{let}\:{find} \\ $$$$\left({x}^{{p}} \right)^{\left({n}\right)} \:\:{for}\:{p}\geqslant{n}\:\:{wehave}\:\left({x}^{{p}} \right)^{\left(\mathrm{1}\right)} ={p}\:{x}^{{p}−\mathrm{1}} \:\:,\left({x}^{{p}} \right)^{\left(\mathrm{2}\right)} ={p}\left({p}−\mathrm{1}\right){x}^{{p}−\mathrm{2}} \\ $$$${so}\:\:\left({x}^{{p}} \right)^{\left({n}\right)} =\:{p}\left({p}−\mathrm{1}\right)….\left({p}−{n}+\mathrm{1}\right){x}^{{p}−{n}} \\ $$$$=\frac{{p}\left({p}−\mathrm{1}\right)….\left({p}−{n}+\mathrm{1}\right)\left({p}−{n}\right)!}{\left({p}−{n}\right)!}\:{x}^{{p}−{n}} \:=\frac{{p}!}{\left({p}−{n}\right)!}\:{x}^{{p}−{n}} \: \\ $$$$\Rightarrow\:\:\left({x}^{\mathrm{2}{k}} \right)^{\left({n}\right)} =\:\:\frac{\left(\mathrm{2}{k}\right)!}{\left(\mathrm{2}{k}−{n}\right)!}\:{x}^{\mathrm{2}{k}−{n}} \:{so} \\ $$$${f}_{{n}} \left({x}\right)=\:\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:\:\frac{\left(\mathrm{2}{k}\right)!}{\left(\mathrm{2}{k}−{n}\right)!}\:{x}^{\mathrm{2}{k}−{n}} \:\:. \\ $$$$ \\ $$
