Question Number 28038 by abdo imad last updated on 19/Jan/18
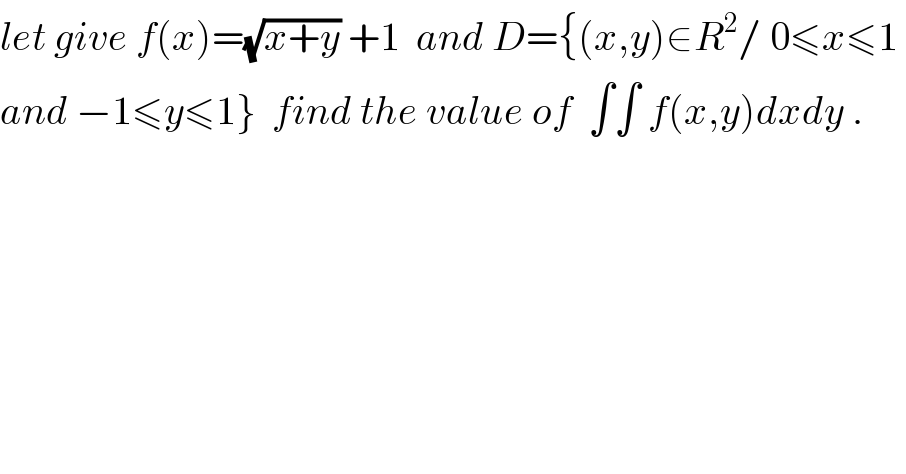
$${let}\:{give}\:{f}\left({x}\right)=\sqrt{{x}+{y}}\:+\mathrm{1}\:\:{and}\:{D}=\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} /\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:\right. \\ $$$$\left.{and}\:−\mathrm{1}\leqslant{y}\leqslant\mathrm{1}\right\}\:\:{find}\:{the}\:{value}\:{of}\:\:\int\int\:{f}\left({x},{y}\right){dxdy}\:. \\ $$
