Question Number 29078 by abdo imad last updated on 04/Feb/18
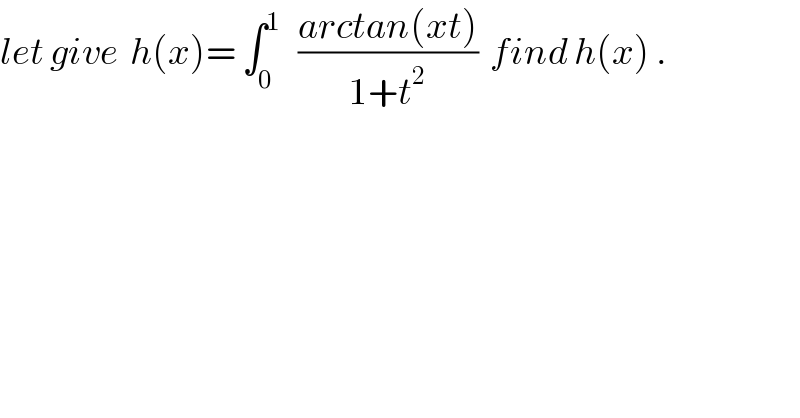
$${let}\:{give}\:\:{h}\left({x}\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{arctan}\left({xt}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:{find}\:{h}\left({x}\right)\:. \\ $$
Commented by abdo imad last updated on 10/Feb/18
![e have h^′ (x) =∫_0 ^1 (t/((1+t^2 )(1+x^2 t^2 )))dt ch xt=u give h^′ (x)= ∫_0 ^x (1/((1 +(u^2 /x^2 ))(1+u^2 ))) (u/x) (du/x) = ∫_0 ^x (u/((x^2 +u^2 )(1+u^2 )))du let decompose F(u)= (u/((x^2 +u^2 )(1+u^2 )))= ((au +b)/(x^2 +u^2 )) +((+αu+β)/(u^2 +1)) F(−u)=−F(u)⇔ ((−au+b)/(u^2 +x^2 )) +((−αu+β)/(u^2 +1)) =((−au−b)/(u^2 +x^2 )) +((−αu−β)/(u^2 +1))⇒b=0 and β=0 F(u)= ((au)/(u^2 +x^2 )) +((αu)/(u^2 +1)) we have lim_(u→∞) uF(u)=0 =a+α ⇒α =−a⇒ F(u)=((au)/(u^2 +x^2 ))−((au)/(u^2 +1)) F(1)= (1/(2(1+x^2 )))= (a/(x^2 +1))−(a/2)=((2a−(1+x^2 )a)/(2(1+x^2 ))) ⇒ (1−x^2 )a=1 ⇒ a=(1/(1−x^2 )) with cond. x^2 ≠1 f^′ (x)= ∫_0 ^x F(u)du =(1/(1−x^2 ))∫_0 ^x ((udu)/(u^2 +x^2 )) −(1/(1−x^2 ))∫_0 ^x ((udu)/(1+u^2 )) =(1/(2(1−x^2 )))[ln(u^2 +x^2 )−ln(1+u^2 )]_0 ^x = (1/(2(1−x^2 )))[ln(((u^2 +x^2 )/(1+u^2 )))]_0 ^x = (1/(2(1−x^2 )))(ln(((2x^2 )/(1+x^2 )))−ln(x^2 )) =(1/(2(1−x^2 )))(ln2 −ln(1+x^2 )) f(x)= ((ln2)/2)∫_0 ^x (dt/(1−t^2 )) −(1/2) ∫_0 ^x ((ln(1+t^2 ))/(1−t^2 ))dt +λ but (1/2)∫_0 ^x (dt/(1−t^2 )) = (1/4)∫_0 ^x ( (1/(1+t)) +(1/(1−t)))dt=(1/4) [ln∣((1+t)/(1−t))∣]_0 ^x =(1/4)ln∣((1+x)/(1−x))∣ f(x) =((ln2)/4)ln∣((1+x)/(1−x))∣ −(1/2) ∫_0 ^x ((ln(1+t^2 ))/((1−t^2 )))dt with cond.x^2 ≠1... be continued...](https://www.tinkutara.com/question/Q29636.png)
$${e}\:{have}\:{h}^{'} \left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)}{dt}\:\:{ch}\:{xt}={u}\:{give} \\ $$$${h}^{'} \left({x}\right)=\:\int_{\mathrm{0}} ^{{x}} \:\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}\:+\frac{{u}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\frac{{u}}{{x}}\:\frac{{du}}{{x}} \\ $$$$=\:\int_{\mathrm{0}} ^{{x}} \:\:\:\:\:\:\:\frac{{u}}{\left({x}^{\mathrm{2}} +{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{du}\:{let}\:{decompose} \\ $$$${F}\left({u}\right)=\:\frac{{u}}{\left({x}^{\mathrm{2}} +{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}=\:\frac{{au}\:+{b}}{{x}^{\mathrm{2}} +{u}^{\mathrm{2}} }\:+\frac{+\alpha{u}+\beta}{{u}^{\mathrm{2}} +\mathrm{1}} \\ $$$${F}\left(−{u}\right)=−{F}\left({u}\right)\Leftrightarrow\:\frac{−{au}+{b}}{{u}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:+\frac{−\alpha{u}+\beta}{{u}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{−{au}−{b}}{{u}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:+\frac{−\alpha{u}−\beta}{{u}^{\mathrm{2}} +\mathrm{1}}\Rightarrow{b}=\mathrm{0}\:{and}\:\beta=\mathrm{0} \\ $$$${F}\left({u}\right)=\:\frac{{au}}{{u}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:+\frac{\alpha{u}}{{u}^{\mathrm{2}} +\mathrm{1}}\:{we}\:{have}\:{lim}_{{u}\rightarrow\infty} {uF}\left({u}\right)=\mathrm{0} \\ $$$$={a}+\alpha\:\Rightarrow\alpha\:=−{a}\Rightarrow\:{F}\left({u}\right)=\frac{{au}}{{u}^{\mathrm{2}} +{x}^{\mathrm{2}} }−\frac{{au}}{{u}^{\mathrm{2}} +\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)=\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}=\:\frac{{a}}{{x}^{\mathrm{2}} +\mathrm{1}}−\frac{{a}}{\mathrm{2}}=\frac{\mathrm{2}{a}−\left(\mathrm{1}+{x}^{\mathrm{2}} \right){a}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right){a}=\mathrm{1}\:\Rightarrow\:{a}=\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:{with}\:{cond}.\:{x}^{\mathrm{2}} \neq\mathrm{1} \\ $$$${f}^{'} \left({x}\right)=\:\int_{\mathrm{0}} ^{{x}} \:{F}\left({u}\right){du}\:=\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\int_{\mathrm{0}} ^{{x}} \:\frac{{udu}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\int_{\mathrm{0}} ^{{x}} \:\:\frac{{udu}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}\left[{ln}\left({u}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)−{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{{x}} \\ $$$$=\:\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}\left[{ln}\left(\frac{{u}^{\mathrm{2}} +{x}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{{x}} =\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}\left({ln}\left(\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\right)−{ln}\left({x}^{\mathrm{2}} \right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}\left({ln}\mathrm{2}\:−{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right) \\ $$$${f}\left({x}\right)=\:\frac{{ln}\mathrm{2}}{\mathrm{2}}\int_{\mathrm{0}} ^{{x}} \:\:\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} }\:\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{x}} \:\:\frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}−{t}^{\mathrm{2}} }{dt}\:+\lambda\:\:{but} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{{x}} \:\:\:\:\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} }\:=\:\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{{x}} \:\left(\:\frac{\mathrm{1}}{\mathrm{1}+{t}}\:+\frac{\mathrm{1}}{\mathrm{1}−{t}}\right){dt}=\frac{\mathrm{1}}{\mathrm{4}}\:\left[{ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid\right]_{\mathrm{0}} ^{{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid \\ $$$${f}\left({x}\right)\:=\frac{{ln}\mathrm{2}}{\mathrm{4}}{ln}\mid\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{x}} \:\:\frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{dt}\:\:{with}\:{cond}.{x}^{\mathrm{2}} \neq\mathrm{1}… \\ $$$${be}\:{continued}… \\ $$
Commented by abdo imad last updated on 10/Feb/18

$$\lambda={f}\left({o}\right)=\mathrm{0} \\ $$
