Question Number 33990 by abdo imad last updated on 28/Apr/18
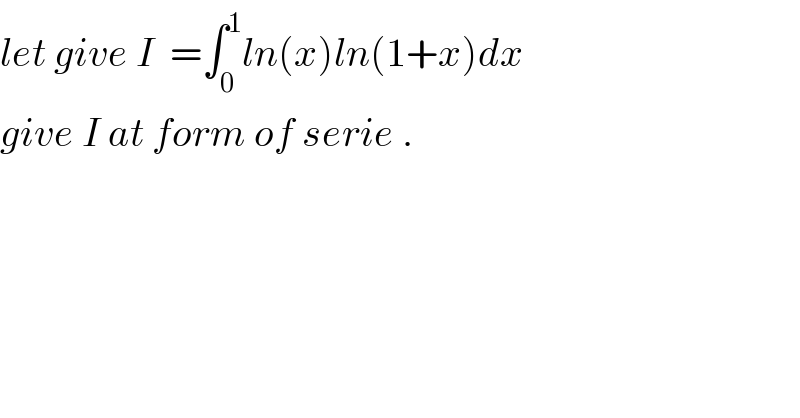
$${let}\:{give}\:{I}\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){ln}\left(\mathrm{1}+{x}\right){dx}\: \\ $$$${give}\:{I}\:{at}\:{form}\:{of}\:{serie}\:. \\ $$
Commented by abdo imad last updated on 01/May/18
![we have ln^′ (1+x)= (1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n with ∣x∣<1 ⇒ln(1+x) =Σ_(n=0) ^∞ (((−1)^n )/(n+1))x^(n+1) +λ =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^n +λ λ=0 ⇒ ln(1+x)=Σ_(n=1) ^∞ (((−1)^(n−1) )/n) x^n I =∫_0 ^1 (Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^n )ln(x)dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^1 x^n ln(x)dx let integrate by parts A_n = ∫_0 ^1 x^n ln(x)dx =[(1/(n+1))x^(n+1) ln(x)]_0 ^1 −∫_0 ^1 (1/(n+1)) x^n dx =−(1/((n+1)^2 )) ⇒ I =−Σ_(n=1) ^∞ (((−1)^(n−1) )/n) (1/((n+1)^2 )) I = Σ_(n=1) ^∞ (((−1)^n )/(n(n+1)^2 )) .](https://www.tinkutara.com/question/Q34128.png)
$${we}\:{have}\:{ln}^{'} \left(\mathrm{1}+{x}\right)=\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \:\:\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$$$\Rightarrow{ln}\left(\mathrm{1}+{x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} \:+\lambda\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{x}^{{n}} \:+\lambda \\ $$$$\lambda=\mathrm{0}\:\Rightarrow\:{ln}\left(\mathrm{1}+{x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{x}^{{n}} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{x}^{{n}} \right){ln}\left({x}\right){dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} {ln}\left({x}\right){dx}\:\:\:{let}\:{integrate}\:{by}\:{parts} \\ $$$${A}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \:{ln}\left({x}\right){dx}\:=\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} {ln}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{{n}+\mathrm{1}}\:{x}^{{n}} {dx} \\ $$$$=−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\:{I}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${I}\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:. \\ $$$$ \\ $$
