Question Number 28985 by abdo imad last updated on 02/Feb/18
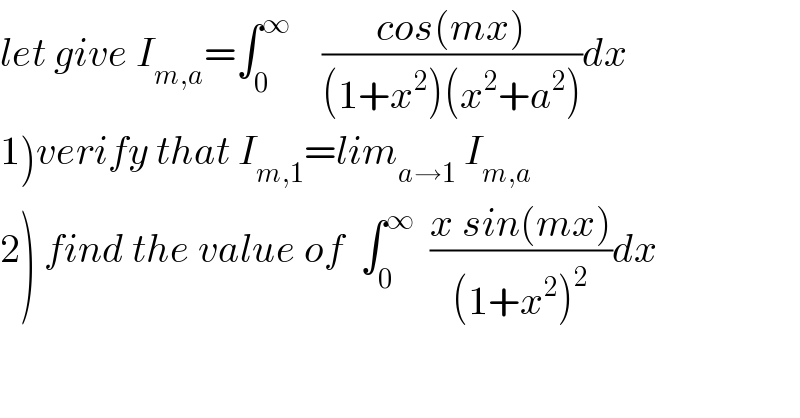
$${let}\:{give}\:{I}_{{m},{a}} =\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{cos}\left({mx}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}{dx} \\ $$$$\left.\mathrm{1}\right){verify}\:{that}\:{I}_{{m},\mathrm{1}} ={lim}_{{a}\rightarrow\mathrm{1}} \:{I}_{{m},{a}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}\:{sin}\left({mx}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$
