Question Number 27666 by abdo imad last updated on 12/Jan/18
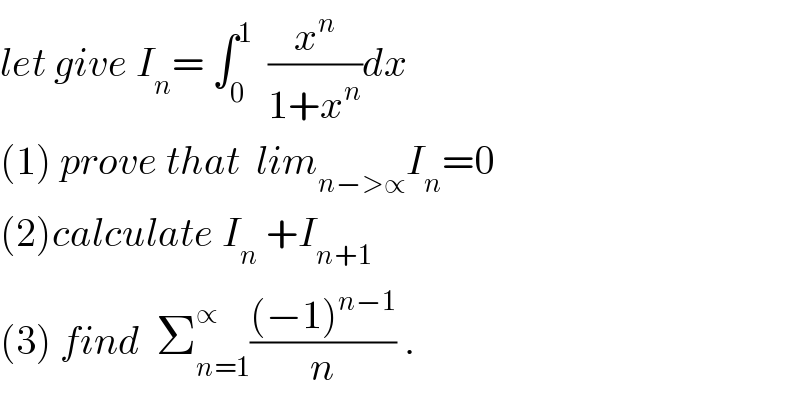
$${let}\:{give}\:{I}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{{n}} }{\mathrm{1}+{x}^{{n}} }{dx} \\ $$$$\left(\mathrm{1}\right)\:{prove}\:{that}\:\:{lim}_{{n}−>\propto} {I}_{{n}} =\mathrm{0} \\ $$$$\left(\mathrm{2}\right){calculate}\:{I}_{{n}} \:+{I}_{{n}+\mathrm{1}} \\ $$$$\left(\mathrm{3}\right)\:{find}\:\:\sum_{{n}=\mathrm{1}} ^{\propto} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:. \\ $$
