let-give-I-x-0-pi-ln-1-2x-cost-x-2-dt-by-using-the-polynomial-p-x-z-x-2n-1-find-the-value-of-I-x-

Tinku Tara June 4, 2023 Integration 0 Comments

Question Number 27794 by abdo imad last updated on 14/Jan/18

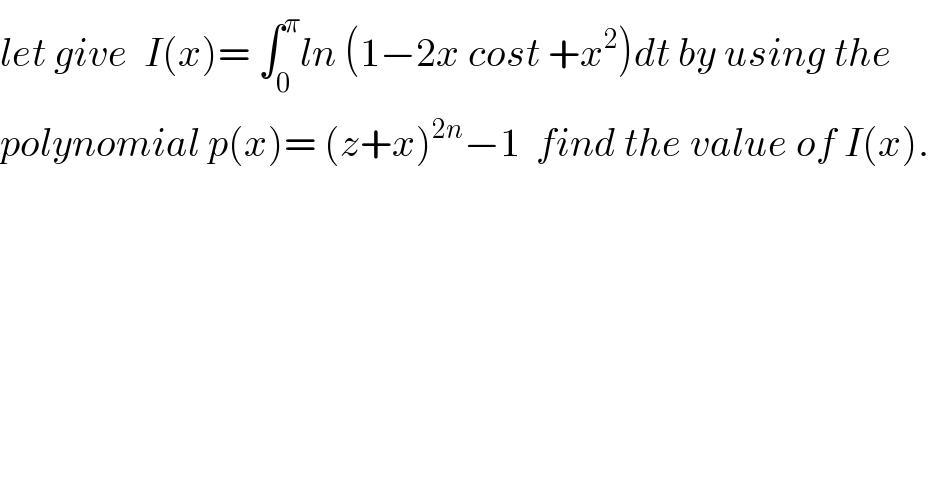
let give I(x)= ∫_0 ^π ln (1−2x cost +x^2 )dt by using the polynomial p(x)= (z+x)^(2n) −1 find the value of I(x).

$${let}\:{give}\:\:{I}\left({x}\right)=\:\int_{\mathrm{0}} ^{\pi} {ln}\:\left(\mathrm{1}−\mathrm{2}{x}\:{cost}\:+{x}^{\mathrm{2}} \right){dt}\:{by}\:{using}\:{the} \\ $$$${polynomial}\:{p}\left({x}\right)=\:\left({z}+{x}\right)^{\mathrm{2}{n}} −\mathrm{1}\:\:{find}\:{the}\:{value}\:{of}\:{I}\left({x}\right). \\ $$

Facebook Tweet Pin

let-give-I-x-0-pi-ln-1-2x-cost-x-2-dt-by-using-the-polynomial-p-x-z-x-2n-1-find-the-value-of-I-x-

Leave a Reply Cancel reply