Question Number 28311 by abdo imad last updated on 23/Jan/18
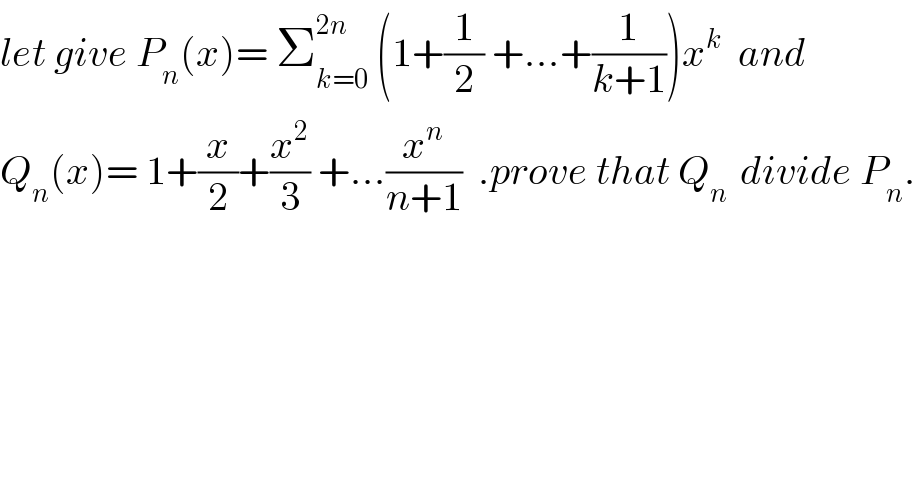
$${let}\:{give}\:{P}_{{n}} \left({x}\right)=\:\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:+…+\frac{\mathrm{1}}{{k}+\mathrm{1}}\right){x}^{{k}} \:\:{and} \\ $$$${Q}_{{n}} \left({x}\right)=\:\mathrm{1}+\frac{{x}}{\mathrm{2}}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}\:+…\frac{{x}^{{n}} }{{n}+\mathrm{1}}\:\:.{prove}\:{that}\:{Q}_{{n}\:} \:{divide}\:{P}_{{n}} . \\ $$
